给定一个整数N，求其N！末尾有多少个0

最新推荐文章于 2021-09-13 14:13:28 发布
原创 最新推荐文章于 2021-09-13 14:13:28 发布 · 2k 阅读 · 3 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

博客围绕给定整数N，求解N！末尾0的个数展开。通过分析10！、15！等示例总结出规律，即找1到N的数字中包含5的个数。还提及了如何用代码实现，包括判断单个数字含5的个数、求N！末尾0的个数及更简便的方式。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

给定一个整数N，求其N！末尾有多少个0？ 例如：N=10，N！=3628800，N！末尾有两个0

解析：
10！为=1x2x3x4x5x6x7x8x9x10
其中2x5=10, 1x10=10,10X10=100,末尾两个0.
15！=1x2x3x4x5x6x7x8x9x10x11x12x13x14x15
其中4x5=10, 1x10=10,2x15=30,10X10x30=3000,末尾3个0
总结规律可得，我们要找N的阶乘末尾有几个0，则找1到N的数字中包含多少个5
但是如何用代码实现呢？
1、先写给定一个数字，判断其中有多少个 5？
在这里插入图片描述
2.再过度到给定一个整数N，求其N！末尾有多少个0？
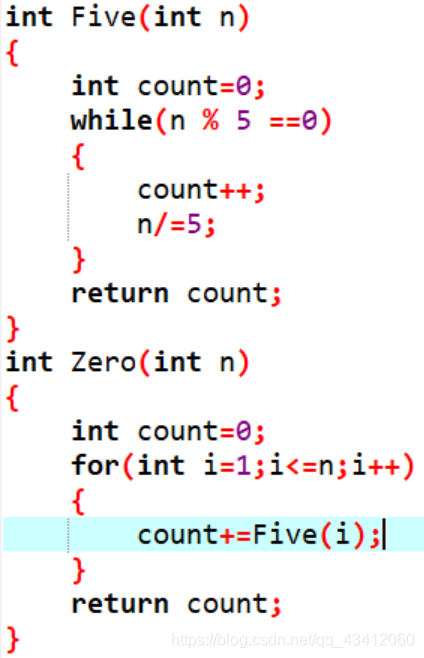
在这里插入图片描述
3、更加简便的方式
在这里插入图片描述

【第22天】给定一个整数 n ，求它的各个数位之和 | 递归与循环
执梗的博客
06-17 6131
【第22天】给定一个整数 n ，求它的各个数位之和 | 递归与循环
【第30天】给定一个整数 n ，求它的因数之和 | 约数之和定理
执梗的博客
07-05 6122
【第30天】给定一个整数 n ，求它的因数之和
求N!末尾0的个数
element137的博客
07-23 2011
题目：给定一个整数N，那么N的阶乘N！末尾有多少个0呢？例如：N＝10，N！＝3 628 800，N！的末尾有两个0。 方法一： 最容易想到的方法，先把N的阶乘求出来，再用一个函数计算末尾0的个数，但是这个方法有两个问题：当数字很大时，效率很差、用内置类型（int、long等）会溢出。要解决这两个问题，只能优化算法。 首先要知道N的阶乘一定可以用K×10M来表示，那我们的问题就变成了
输入有一个正整数n，求n！末尾有多少个0？
qq_45852612的博客
04-21 1581
题目描述 输入有一个正整数n，求n！末尾有多少个0？比如：n=10；n！=3628800，所以答案为2 思路：末尾0的个数实际上就是2*5的个数，2肯定比5多，所以现在就统计5的个数 代码实现 public static void main(String[] args) { System.out.print("->"); Scanner sc = new Scanner(System.in); int n = sc.nextInt();
输入一个正整数n,求n!(即阶乘)末尾有多少个0？ 比如: n = 10; n! = 3628800,所以答案为2
shoushou_的博客
11-18 2399
输入描述: 输入为一行，n(1 ≤ n ≤ 1000) 输出描述: 输出一个整数,即题目所求 示例1 输入 10 输出 2 分析： 任意挑选几个数字进行分解质因数，例如： 6 = 23 15 = 35 64 = 222222 = 2^6 100 = 2^2 * 5^2 576 = 2^6 * 3^2 那么我们在计算n的阶乘时，实际上就是把所有小于等于n的正整数分解成质因数，然后再将其乘到一起，那么...
判断N!末尾有多少个0
dcjhyn的博客
07-23 8987
问题：N的阶乘(N!)中的末尾有多少个0? 例如: N = 5,N! = 120.末尾有1个0. N = 10，N! = 3628800.末尾有2个0。分析:看到这个问题，有人可能第一反应是先求出N!,然后再根据求出的结果，最后得出N!的末尾有多少个0。但是转念一想，会不会溢出。其实，从”哪些数相乘可以得到10”这个角度，问题就变得比较的简单了。 首先考虑，如果N的阶乘为K和10的
n!的末尾0的个数
Demons的博客
07-30 4048
题目描述： 输入一个正整数n,求n!(即阶乘)末尾有多少个0？ 比如: n = 10; n! = 3628800,所以答案为2 。 解题思路： 对于这样的问题，我们可以换个思维方式，它要求0的个数，那么0是怎么来的？ 是不是一对2*5得到的0，所以我们可以分解这个问题分，把他看作是求整数n分解质因数后，一共有多少组min(2,5)，在当然2的个数肯定比5多，所以我们继续往...
n的阶乘末尾有多少个0_n的阶乘末尾的0_
10-03
在给定的文件列表中，“n的阶乘末尾有多少个0.cpp”可能是实现这个算法的C++源代码，而“n的阶乘末尾有多少个0.exe”是编译后的可执行文件，用于直接运行程序并得到结果。 通过这种方法，我们可以有效地处理大数...
给定一个整数N，求解整数N！末尾0的个数
01-02 722
问题描述 1、给定一个整数N，阶乘N！末尾有多少个0 2、求N！的二进制表示中最低位1的位置 1、给定一个整数N，阶乘N！末尾有多少个0 举例：10！＝3 628 800，则 N！的末尾有两个0 思路：   即，知道 Z ，就知道N！中含有0的个数 方法一：求出1~N中每一个数被5整除的因子的个数，比较笨 代码： [cpp
C++版本计算n阶乘末尾0的个数原理讲解及代码实现
07-10
本篇文章主要介绍如何使用C++编程语言来计算一个正整数n的阶乘末尾0的数量，并通过示例代码加以说明。该方法不仅阐述了理论基础，还提供了具体的实现思路。 #### 原理讲解 ##### 计算末尾0的数量 为了理解如何计算...
数字操作：172. 阶乘后的零
aishenla的博客
10-29 486
给定一个整数 n，返回 n! 结果尾数中零的数量。 示例 1: 输入: 3 输出: 0 解释:3! = 6, 尾数中没有零。 示例2: 输入: 5 输出: 1 解释:5! = 120, 尾数中有 1 个零. 解法一 首先肯定不能依赖于把阶乘算出来再去判断有多少个零了，因为阶乘很容易就溢出了，所以先一步一步理一下思路吧。 首先末尾有多少个 0 ，只需要给当前数乘以一个 10 就可以加一个 0。 再具体对于 5!，也就是 5 * 4 * 3 * 2 * 1 = 120，我们发现结果会有一个 ...
给定一个整数N,那么N！末尾有多少了0
03-10 1206
例如N=10，N！=3628800  末尾有两个零 题目表面看起来很简单，就是要求因式分解后因子有几个5,5X2=10, 只要是偶数就有2这个因子，显然5的个数就代表了N！结果中末尾0的个数 起初我的思路是含有N/5个0，没有考虑到5的次方的问题，导致了问题的错误 正确的解法应该是，先算N/5，则有N/5个5，同时考虑N/5^2 ..... 例如N=1000 N/5 = 200 20
【编程之美】读书笔记：给定一个整数N，求N!末尾有多少个0
xiaoding133的专栏【Stay hungry,Stay foolish】
10-01 4160
问题：给定一个整数N，求N!末尾有多少个0          这个题目不能直接求出N!的值，这样可能会溢出。首先考虑N!=K*10^M,并且K不能被10整除，那么N!末尾有M个0。再考虑对N！进行质因数分解，N！=(2^X)*(3^Y)*(5^Z)...,由于10=2*5，所以M只和X和Z有关，每一对2和5相乘都可以得到一个10，于是M=min(X,Z);不能看出X>=Z.所以把公式简化为M=Z
编程之美3——N!末尾有多少个0
weixin_33730836的博客
04-11 122
因为n!是一个非常大的数，所以不能通过常规的方法，求出n!的值之后，再判断它的末尾有多少个0.这里的关键就是，n!的末尾有多少个0，取决于n!中，质因数 5 的个数。如：12!=479001600 ，其中，5、10各含有1个质因数5，所以12!末尾有2个0代码1:#include<iostream> usingnamespacestd; intmai...
给定一个整数N，那么N的阶乘N！末尾有多少个0
centor的博客
09-19 1282
//例如：N＝10，N！＝3 628 800，N！的末尾有两个0。 //如果N是一个很大的数，它的阶乘可能已超出计算机所能计算的最大范围，因此可能会导致溢出。 //我们换个角度想， N！=1×2×3×4×5×6×··· ×N //我们可以对N！进行分解质因数，即 //N！=（2^x）×(3^y)×(5^z) ·········· //可以看到2和5相乘必然会产生一个10，而这个10会在阶乘
简单求一个数字尾部零的个数
阿牛哥的博客
05-28 1281
求一个数字尾部零的个数 例如：n=2021202000 输出：3 算法思路：数字的最后一位求出并判断是否为零，并且每次判断后就缩小（去掉这个尾部零），再接着判断到第一次判断出这个不符合条件的就给他break。 代码描述： #include <stdio.h> #include <math.h> int main() { int m,count =0,n = 201090000; while(n!=0){ m = n%10;//得到最后一位数字赋值给m if(
阶乘后的零，给定一个整数 n，返回 n! 结果尾数中零的数量。
weixin_45745641的博客
09-13 604
题目描述 阶乘后的零，给定一个整数 n，返回 n! 结果尾数中零的数量。 示例 1: 输入: 3 输出: 0 解释: 3! = 6, 尾数中没有零。 示例 2: 输入: 5 输出: 1 解释: 5! = 120, 尾数中有 1 个零. 解析： 仅有X5*2的倍数可以形成尾部0，容易理解2的倍数要多于型为X5的因子，所以统计5^i的个数即可 int trailingZeroes(int n){ int res=0; do{ res+=n/5; n=n/5;
输入一个正整数n，求n!末尾有多少个0
say67033的博客
08-31 4310
思路： 1）按正常思路，我先求出n的阶乘，但是这样做，会使得结果溢出，从而得不到最后的结果。以下是求阶乘的代码，递归。 public static long getNFactorial(int n){         if(n==0){             return 1;         }         return n*getNFactorial(n-1); } ...
n的阶乘(n!)末尾有多少个0
weixin_30455067的博客
09-30 216
给定一个数n，求其阶乘的末尾有多少个0。 末尾为0的产生原因是阶乘中出现了含有因子为2、5的数。含有因子为2的数，即偶数，远远多于含有因子为5的数。因此求出有多少个5的倍数就可以了，n/5。 这只考虑了两个数相乘末尾为一个0的情况，如2*5，但是还有两个数相乘末尾为两个0、三个0； 末尾有两个零是因为有因子4和25，末尾有三个0是因为有因子8、125。。。 这样可以写出公式 程序实...
给定一个整数 n，返回 n! 结果尾数中零的数量
05-05
要计算 n! 结果尾数中零的数量，我们需要找到所有质因子为 5 的数的个数。因为每个质因子 5 都会贡献一个因子 10，而每个因子 10 又会贡献一个末尾的零。因此，我们可以先计算 n! 中所有数的质因子中因子 5 的个数，然后将它们加起来即可。 具体地，我们可以将 n! 写成如下形式： n! = 1 * 2 * 3 * ... * (5 * k) * ... * n 其中，5 * k 是所有小于等于 n 的数中因子 5 的个数。那么，我们只需要计算 5 * k 的个数即可。 假设 n 中包含 k 个因子 5，则我们可以将 n 写成： n = 5^k * m 其中，m 是不包含因子 5 的数。因此，我们可以得到： n! = 1 * 2 * 3 * ... * 5^k * m * ... * n 其中，5^k 是所有小于等于 n 的数中因子 5 的个数。因此，我们只需要计算 k 的值即可。 具体地，我们可以使用如下代码实现： ```python def trailingZeroes(n: int) -> int: count = 0 while n > 0: count += n // 5 n //= 5 return count ``` 这里我们使用了一个 while 循环来计算 n 中包含的因子 5 的个数。每次将 n 除以 5 取整数部分，然后将这个数加到 count 中。最后将 n 除以 5 取整数部分，重复这个过程，直到 n 小于 5。最后返回 count 即可。 例如，当 n = 25 时，我们有： 25! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 * 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20 * 21 * 22 * 23 * 24 * 25 其中，包含 5 的数有 5、10、15、20、25，共 5 个。又因为 25 包含两个因子 5，因此总共包含 6 个因子 5。因此，trailingZeroes(25) 的返回值为 6。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值