
Abstract
本文研究了在低维向量空间中嵌入超大规模信息网络的问题
动机: 现有的大多数图嵌入方法都不适用于通常包含数百万个节点的真实信息网络。本文提出了一种新的网络嵌入方法,称之为“LINE”, 它适用于任意类型的信息网络:无向、有向和/或加权。
代码获取:https://github.com/tangjianpku/LINE
亮点
LINE 算法对所有的**一阶近似(节点6和7,有边连接)和二阶近似节点(节点5和6,有相似的邻居)**对进行了概率建模,利用二阶近似的考虑有效地补充了一阶近似的稀疏性,更好地保持了网络的全局结构。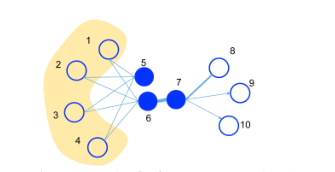
最后,整合一阶和二阶节点相似性,引入一个目标函数,使得学习到的节点 embedding分布更加的均衡平滑。
paper贡献
- 提出了一种新的网络嵌入模型,称为“线”,它适用于任意类型的信息网络,并且易于扩展到数百万个节点。它有一个精心设计的目标函数,保留了一阶和二阶近似。
- 提出了一种优化目标的边缘采样算法。该算法克服了经典随机梯度下降的局限性,提高了推理的有效性和效率。
- 在现实世界的信息网络上进行广泛的实验。实验结果证明了本文提出的直线模型的有效性和有效性。
模型
注:本文只考虑非负权重的边
一阶近似(只适用于无向图)
该模型只适用于无向图,对于一条无向边(i,j),那么定义该边的两个端点vi和vj的共享概率如下: p1(vi,vj)=1/1+exp(−uTi.uj) 其中ui和uj就是点i和j的向量化表示形式,这个相当于从Embedding的角度来描述点之间的亲密程度。那么实际上从网络的结构数据也能得到关于两个点亲密程度的度量,p2(vi,vj)=wij/W,其中wij代表了点i和j之间的边的权值,W代表了网络中所有边权值的和。 优化目标就是分布p1和p2差异性越小越好,即目标函数如下所示: O=d(p1,p2),这个d()函数用来衡量两个分布之间的差异性,一般可以选用KL散度,将KL散度带入上式再去掉一些固定项,就可以得到最终的优化形式:O=−∑(i,j)∈Ewijlogp1(vi,vj)。
对于每个无向边(i,j),他们的连接可能性:
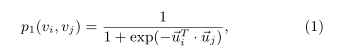
经验概率:
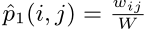
其中:
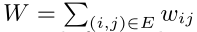
KL-divergence :两个分布之间的距离:
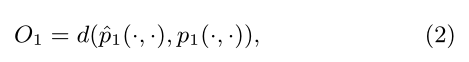
化简后最小化该目标函数即可:
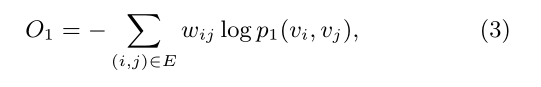
二阶近似(适用于有向图和无向图)
二阶近似假设共享多个连接到其他顶点的顶点彼此相似。在这种情况下,每个顶点也被视为一个特定的“上下文”,并且假设在“上下文”上具有相似分布的顶点是相似的。因此,每个顶点都扮演两个角色:**顶点本身和其他顶点的特定“上下文”。**作者引入两个向量 u→^→→i_ii和u→^→→i_ii’,分别表示顶点Vi_ii作为顶点时和作为上下文时的表示。
对于每个有向边(i,j),首先定义由顶点Vi_ii产生上下文Vj_jj的可能性(:
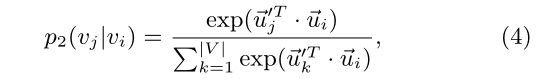
经验概率(亲密程度可以按照该式衡量):
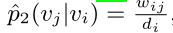
di_ii为顶点i的出度
同样为了使分布p1和p2的差异性最小化,KL-divergence化简优化:得到d维向量来表示每个顶点
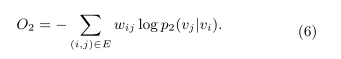
优化
Negative sampling
由于计算2阶相似度时,softmax函数的分母计算需要遍历所有顶点,这是非常低效的,论文采用了负采样优化的技巧,目标函数变为:
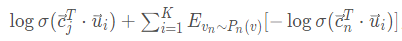
K是负边的个数。负采样概率:
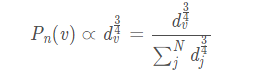
d是顶点的出度_是顶点的出度是顶点的出度
更新:
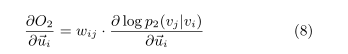
Edge Sampling
注意到我们的目标函数在log之前还有一个权重系数wi_iij_jj,在使用梯度下降方法优化参数时,wi_iij_jj会直接乘在梯度上。如果图中的边权方差很大,则很难选择一个合适的学习率。若使用较大的学习率那么对于较大的边权可能会引起梯度爆炸,较小的学习率对于较小的边权则会导致梯度过小。
一种方法则是从原始的带权边中进行采样,每条边被采样的概率正比于原始图中边的权重,这样既解决了学习率的问题,又没有带来过多的存储开销。
这里的采样算法使用的是Alias算法

LINE思考:
1.度数很低的顶点如何处理?
这样的节点的邻居数量非常少,所以很难精确地推断它的表示,特别是基于二阶相似度的方法。
解决方案是通过添加更高阶的邻居扩展这些顶点的邻居,例如将节点邻居的邻居作为节点的邻居。LINE中只考虑向每个顶点添加二阶邻居,即邻居的邻居。顶点i与其二阶邻居j之间的权重被测量为:

2.新加入的顶点如何处理?
新加入节点i与已有节点的连接已知的情况:可以得到经验分布p1(·,vi)和p2(·| vi),然后可以通过最小化下面的任一目标函数得到新节点的向量表示(已有节点的向量表示保持不变)






 本文介绍了一种名为LINE的网络嵌入方法,适用于各种信息网络,包括无向、有向和加权网络。LINE通过一阶和二阶近似建模节点间的概率,保持网络全局结构,适用于大规模网络。实验验证了其有效性和效率。
本文介绍了一种名为LINE的网络嵌入方法,适用于各种信息网络,包括无向、有向和加权网络。LINE通过一阶和二阶近似建模节点间的概率,保持网络全局结构,适用于大规模网络。实验验证了其有效性和效率。

















 1530
1530

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








