java简单实现二叉树

首先，我们来讲讲什么是树：

树是一种非线性的数据结构，相对于线性的数据结构(链表、数组)而言，树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高)
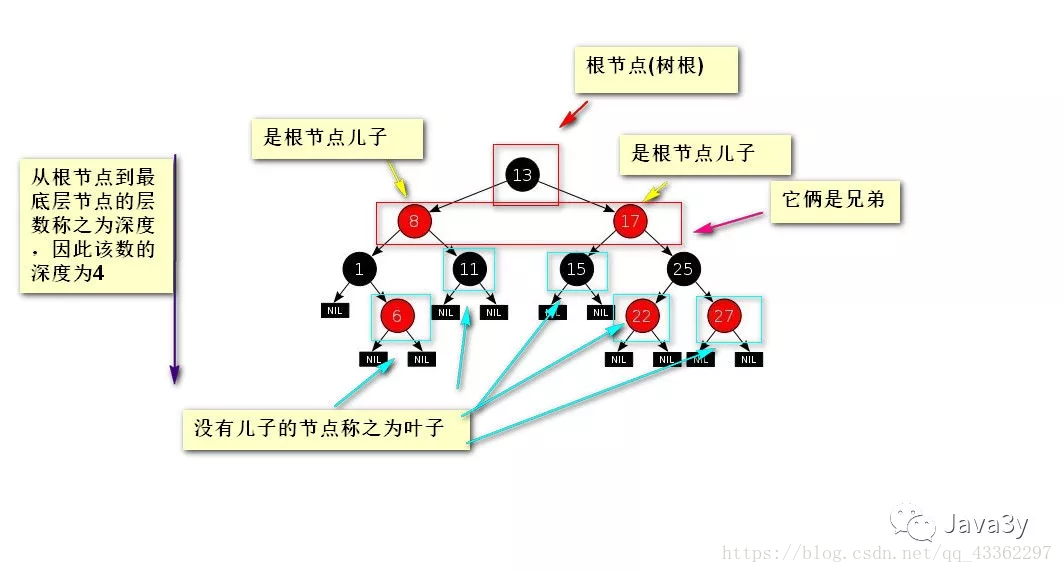
但是在编程的世界中，我们一般把树“倒”过来看，这样容易我们分析：

一般的树是有很多很多个分支的，分支下又有很多很多个分支，如果在程序中研究这个会非常麻烦。因为本来树就是非线性的，而我们计算机的内存是线性存储的，太过复杂的话我们无法设计出来的。

因此，我们先来研究简单又经常用的—> 二叉树
1.1树的一些概念
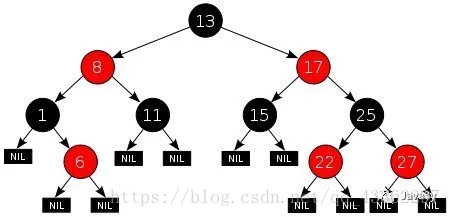
我就拿上面的图来进行画来讲解了：

二叉树的意思就是说：每个节点不能多于有两个儿子，上面的图就是一颗二叉树。

一棵树至少会有一个节点(根节点)

树由节点组成，每个节点的数据结构是这样的：

因此，我们定义树的时候往往是->定义节点->节点连接起来就成了树，而节点的定义就是：一个数据、两个指针(如果有节点就指向节点、没有节点就指向null)
1.2静态创建二叉树
上面说了，树是由若干个节点组成，节点连接起来就成了树，而节点由一个数据、两个指针组成

因此，创建树实际上就是创建节点，然后连接节点

首先，使用Java类定义节点：
public class TreeNode {

// 左节点(儿子)
private TreeNode lefTreeNode;

// 右节点(儿子)
private TreeNode rightNode;

// 数据
private int value;

}
为了方便构建，我就给了它一个带参数的构造方法和set、get方法了：

public TreeNode(int value) {

    this.value = value;
}

那么我们现在就创建了5个节点：

public static void main(String[] args) {

    //根节点-->10
    TreeNode treeNode1 = new TreeNode(10);

    //左孩子-->9
    TreeNode treeNode2 = new TreeNode(9);

    //右孩子-->20
    TreeNode treeNode3 = new TreeNode(20);

    //20的左孩子-->15
    TreeNode treeNode4 = new TreeNode(15);

    //20的右孩子-->35
    TreeNode treeNode5 = new TreeNode(35)        

}

它们目前的状态是这样子的：

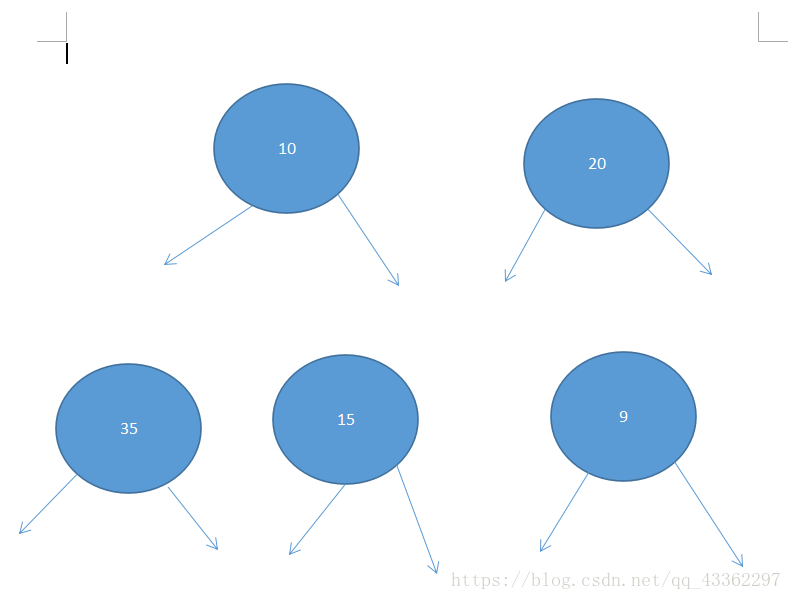
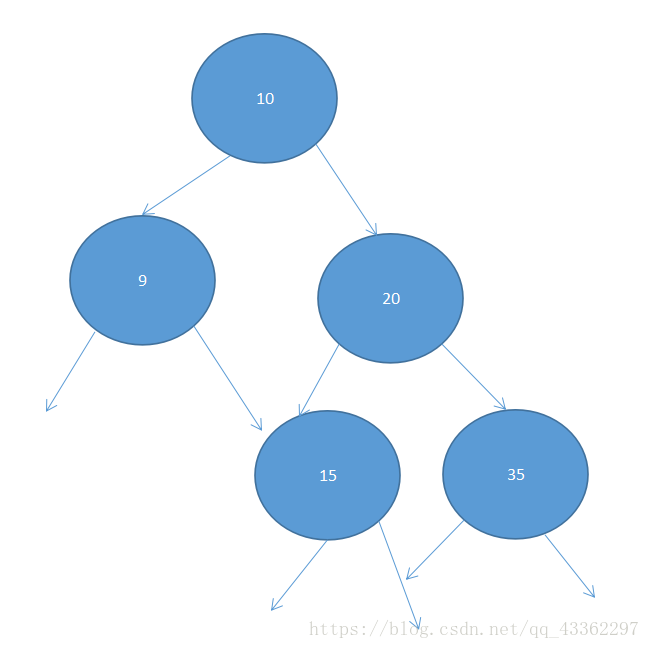
于是下面我们去把它连起来：

//根节点的左右孩子
treeNode1.setLefTreeNode(treeNode2);
treeNode1.setRightNode(treeNode3);

//20节点的左右孩子
treeNode3.setLefTreeNode(treeNode4);
treeNode3.setRightNode(treeNode5);

1.3遍历二叉树
上面说我们的树创建完成了，那怎么证明呢？？我们如果可以像数组一样遍历它(看它的数据)，那就说明它创建完成了～

值得说明的是：二叉树遍历有三种方式

中序遍历

先访问根节点，然后访问左节点，最后访问右节点(根->左->右)

先序遍历

先访问左节点，然后访问根节点，最后访问右节点(左->根->右)

后序遍历

先访问左节点，然后访问右节点，最后访问根节点(左->右->根)

以上面的二叉树为例：

如果是中序遍历：10->9->20->15->35

如果是先序遍历：9->10->15->20->35

可能需要解释地方：访问完10节点过后，去找的是20节点，但20下还有子节点，因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就返回20节点，访问20节点。最后访问35节点

如果是后序遍历：9->15->35->20->10

可能需要解释地方：先访问9节点，随后应该访问的是20节点，但20下还有子节点，因此先访问的是20的左儿子15节点。由于15节点没有儿子了。所以就去访问35节点，由于35节点也没有儿子了，所以返回20节点，最终返回10节点

一句话总结：中序(根->左->右)，先序(左->根->右)，后序(左->右->根)。如果访问有孩子的节点，先处理孩子的，随后返回

无论先中后遍历，每个节点的遍历如果访问有孩子的节点，先处理孩子的(逻辑是一样的)

因此我们很容易想到递归

递归的出口就是：当没有子节点了，就返回

因此，我们可以写出这样的中序遍历代码：

/**
 * 中序遍历
 * @param rootTreeNode  根节点
 */
public static void inTraverseBTree(TreeNode rootTreeNode) {

    if (rootTreeNode != null) {

        //访问根节点
        System.out.println(rootTreeNode.getValue());

        //访问左节点
        preTraverseBTree(rootTreeNode.getLefTreeNode());

        //访问右节点
        preTraverseBTree(rootTreeNode.getRightNode());
    }
}

结果跟我们刚才说的是一样的：
10
9
20
15
35
我们再用先序遍历调用一遍吧：

/**
 * 中序遍历
 * @param rootTreeNode  根节点
 */
public static void preTraverseBTree(TreeNode rootTreeNode) {

    if (rootTreeNode != null) {

        //访问左节点
        preTraverseBTree(rootTreeNode.getLefTreeNode());

        //访问根节点
        System.out.println(rootTreeNode.getValue());

        //访问右节点
        preTraverseBTree(rootTreeNode.getRightNode());
    }
}

结果跟我们刚才说的是一样的：
9
10
15
20
35
有意思的是：通过先序和中序或者中序和后序我们可以还原出原始的二叉树，但是通过先序和后续是无法还原出原始的二叉树的

也就是说：通过中序和先序或者中序和后序我们就可以确定一颗二叉树了！