120. 三角形最小路径和------动态规划

这道题的历史比较悠久了，可以说是经典的动态规划的题型。
说到**动态规划** ,我们就来回忆一下什么叫动态规划。

官方定义：

动态规划是把一个大问题拆解成一 堆小问题，这个本身没啥问题，但是我觉得的这个不是动态规划的核心思想，或者说，个” 大问题”之所以能用” 动态规划"解决，并不是因为它能拆解成一 堆小问题，事实上啥大问题都能拆解成小问题…

接地气的说法

就是从一个好解决的小问题出发，当我解决了n个小问题后，这个大问题的答案就是出来了。但是并不是每个问题都能这样拆分的。

案例

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。


例如，给定三角形：

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

首次看到这个题像极了二叉树

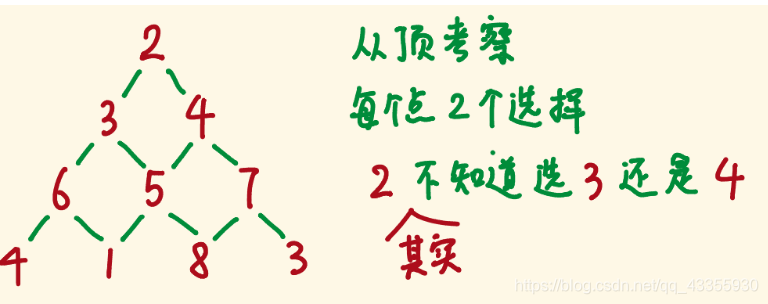
这样也行还是抽象了一些可以变成三角行的方式

思路

我们可以自底向上一次计算最小和，当到达最顶尖的位置时，刚刚就是这个大问题的解。
那么可以创建一个dp[ ],将原数组的底边的所有值push到dp的底边，依次向上求最小和，以例子作为讲解：

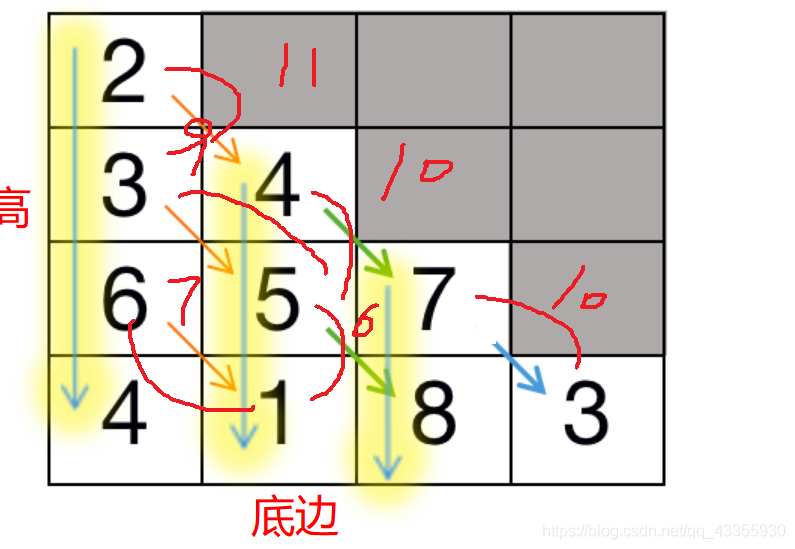
3+7=10,8+7=15 10<15，所以选个3 即原数组7的位置，dp就是10
1+5=6,8+7 = 15 6<15,所以选个1,即原数组5的位置，dp就是6

4+6=10,1+6=7,10>7,所以选个1 即原数组6的位置，dp就是7
···
···
···
即塔尖就是 9+2=11,10+2=12 ，11<12 ，所以最终返回11

具体代码

/**
 * @param {number[][]} triangle
 * @return {number}
 */
var minimumTotal = function(triangle) {
    //定义三角形的宽和高
    let height = triangle.length;
    let width = triangle[0].length;
    //初始化数组
    let dp = new Array(height);

    for (let i = 0; i < height; i++) {
    //初始为0
        dp[i] = new Array(width).fill(0)
    }
    //dp
    for (let i = height - 1; i >= 0; i--) {
        for (let j = triangle[i].length - 1; j >= 0; j--) {
            //将三角形的底边初始到dp的底边
            if (i == height - 1) {
                dp[i][j] = triangle[i][j];
            } else {
                //看这个(相邻节点)的和，那个小，把小的那个相加
                dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle[i][j]
            }
        }
    }
   // dp
    return dp[0][0]
};