关于二分查找LeetCode刷题总结（上）

首先来谈一下二分查找的模板问题。一般会出现一下三种错误：
1、数组越界。
2、死循环
3、跳过查询的元素下标。

先来看几组常见容易出错的模板。

int low=0,high=n;
while(low<high)
{
int mid=low+(high-low)/2;
if(…)
low=mid;
else
high=mid;
}

这种情况下，如果在[2,2]中找值为3的下标，那么每次都会让low的值等于mid，使low和high紧挨在一起，永远也退不出去，造成死循环。

那如果我每次让它进1减1尼？

int low=0,high=n;
while(low<high)
{
int mid=low+(high-low)/2;
if(…)
low=mid+1;
else
high=mid-1;
}

这总不会出问题了吧。。。可还是会出问题。还是例子说话，比如说[1,2，2,3]里找最后一个值为2的元素。有这样的二分查找程序

 int low=0,high=n;
while(low<high)
{
   int mid=low+(high-low)/2;
   if(a[mid]<=mid)
   low=mid+1;
   else
   high=mid-1;
   }
  //根据条件返回low和high

会出现什么结果尼？

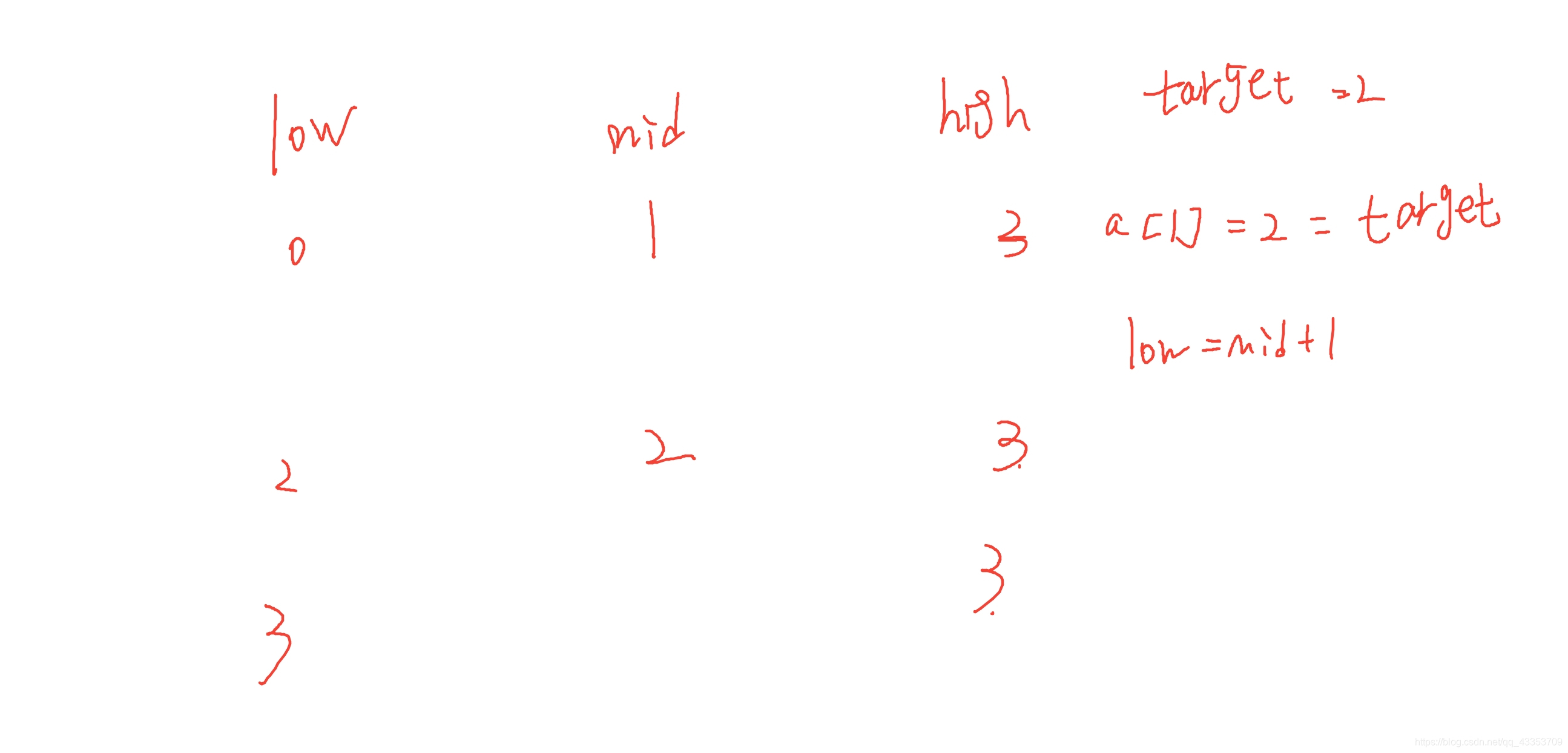
返回来的是下标为3的值，而不是2。（为什么不能返回mid？多加几个2试一下就可以知道返回mid也不满足题目要求）。

接下来就是现在最常见的版本

int low=0,high=n;
while(low<=high)
{
int mid=low+(high-low)/2;
if(…)
low=mid+1;
else
high=mid-1;
}

这时这个模板已经很完美了，只要数组的长度不为0时，等式永远成立，但还是存在一定缺陷的，比如[1]中找0元素，那么high会变成-1，导致溢出，所以通常还要加地址合法判断条件，但毕竟也不是什么大问题。

最后讲到模板问题，虽然解决问题时应该随机应变，根据具体问题调整。但一个好的模板能让我们不用去关心代码内部实现，大大降低了我们解决问题时的思维复杂度。

int low=0,high=n;
while(low+1<high)
{
int mid=low+(high-low)/2;
if(…)
low=mid;
else
high=mid;
}

这个模板的优点在于，low和high是紧挨着的两个下标，我们不用关心是否需要mid+1/-1，自然也不需要担心low/high会越界，只需要具体问题套模板即可。

下面具体在练习题中体会各个模板在实现具体问题的不同。

LeetCode 278题 第一个错误的版本。
你是产品经理，目前正在带领一个团队开发新的产品。不幸的是，你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的，所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

版本一

// Forward declaration of isBadVersion API.
bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
        if(n==1) return n;
        else
        {
            int low=1,high=n;
            while(low<=high)
            { int mid=low+(high-low)/2;
                if(isBadVersion(mid))
                     high=mid-1;
                else low=mid+1;
            }
            return low;
        }
    }
};

版本二

bool isBadVersion(int version);

class Solution {
public:
    int firstBadVersion(int n) {
     
       
        
            int low=1,high=n;
            while(low+1<high)
            { int mid=low+(high-low)/2;
                if(isBadVersion(mid))
                     high=mid;
                else low=mid;
            }
            if(isBadVersion(low)) return low;
            else return high;
        
    }
};

对比两个版本来说，版本一需要判定n的值是否为1（为1时二分查找下标会越界），而版本二则避免了这个问题。

LeetCode34题 在排序数组中查找的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值，返回 [-1, -1]。
示例 1:
输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]
示例 2:
输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

版本一

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> result;
        result.resize(2);
        result[0]=-1;
        result[1]=-1;
        int n=nums.size();
        if(n==0)  return result;
            int low=0,high=n-1,slow=0,shigh=n-1;
        while(low+1<high)
        { int mid=low+(high-low)/2;
            if(nums[mid]>=target)
                {
                     high=mid;

                }
                else low=mid;
            
        }
        if(nums[low]==target)
         result[0]=low;
         else if(nums[high]==target)
         result[0]=high;

        while(slow+1<shigh)
        { int mid=slow+(shigh-slow)/2;
               if(nums[mid]<=target)
                    slow=mid;
                else shigh=mid;
        }
       if(nums[shigh]==target)
         result[1]=shigh;
        else if(nums[slow]==target)
         result[1]=slow;
        return result;
       }
};

版本二

class Solution {
public:
	vector<int> searchRange(vector<int>& nums, int target) {
		vector<int> result;
		result.resize(2);
		int n = nums.size();
		result[0] = -1;
		result[1] = -1;
		if (n == 0)  return result;
		if (n == 1)
		{
			if (nums[n - 1] == target)
			{
				result[0] = 0;
				result[1] = 0;
			}

			return result;
		}
		else
		{
			int low = 0, high = n - 1, slow = 0, shigh = n - 1;
			while (low <= high)
			{
				int mid = low + (high - low) / 2;

				if (nums[mid] >= target)
				{
					high = mid - 1;

				}
				else
					low = mid + 1;
			}

			if (low>n-1)//[2,2]找2时high=-1，找3时low=2，所以当low越界时，就表明数组中无此元素。
				return result;
			if (nums[low] == target)
			{
				result[0] = low;
			}
			else return  result;

			while (slow <= shigh)
			{
				int mid = slow + (shigh - slow) / 2;
				if (nums[mid] <= target)
					slow = mid + 1;
				else shigh = mid - 1;
			}

			if (shigh<0)  return result;
			if (nums[shigh] == target)
			{
				result[1] = shigh;

			}

			return result;
		}
	}
};

相比较于版本一，版本二就更繁琐一些了，不仅需要判断数组中只为一个元素时的情况，而且还需要预防数组越界的情况，实现时需要考虑的细节比较多，相比较下，还是版本一的模板更方便些。

240 搜索二维矩阵||
**编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性：
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
示例:
现有矩阵 matrix 如下：
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5，返回 true。
给定 target = 20，返回 false。

思路：本题有一个巧妙的解法，我们可以从右上角或者左下角开始搜索，当前元素大于targe时。

当当前下标元素值小于targe时

这样我们每次都可以遍历一行或者一列，时间复杂度为O（row+col）

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        
        if(matrix.empty()||matrix.size()==0||matrix[0].size()==0)  return false;
        else
        {
             int row=matrix[0].size();
             int col=matrix.size();
             int x=0,y=row-1;
             while(x<col&&y>=0)
             {
                 if(matrix[x][y]==target) return  true;
                 else if(matrix[x][y]>target)
                         y--;
                 else  x++;
             }
             return false;
    
        
    }
    }
};