LeetCode刷题笔记【困难】

最新推荐文章于 2022-01-04 23:08:50 发布

qq_43313035

最新推荐文章于 2022-01-04 23:08:50 发布

阅读量464

点赞数 1

CC 4.0 BY-SA版权

分类专栏： LeetCode刷题

本文链接：https://blog.youkuaiyun.com/qq_43313035/article/details/95348299

LeetCode刷题专栏收录该内容

5 篇文章

订阅专栏

本文精选了包括柱状图最大矩形、戳气球、接雨水等在内的多项经典算法题目，详细解析了每道题目的解题思路及代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

柱状图中最大的矩形

问题描述：
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

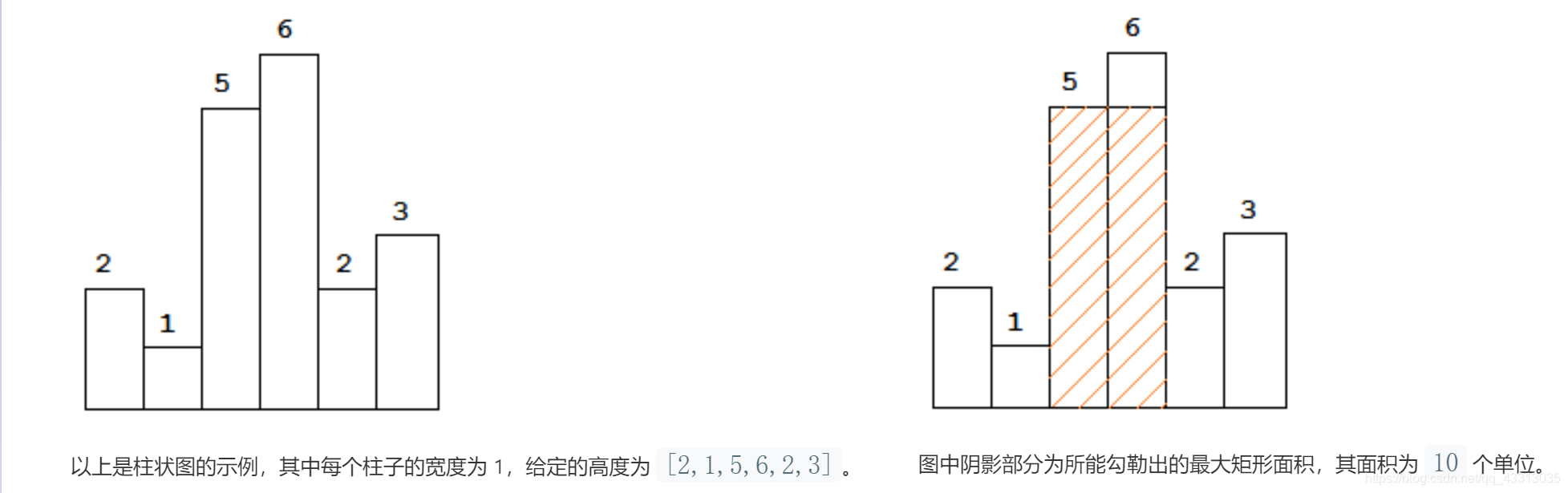
在这里插入图片描述

解题思路：

这道题的最优解法是使用单调栈，时间复杂度可以达到 $O (n)$

单调栈：栈内元素单调递增或单调递减的栈(本题我们使用单调递增的栈)
单调栈的维护是 $O (n)$ 级的时间复杂度，因为所有元素只会进入栈一次，并且出栈后再也不会进栈了。
单调栈的性质
单调栈里的元素具有单调性
元素加入栈前，会在栈顶端把破坏栈单调性的元素都删除。
使用单调递增栈可以找到元素向左遍历第一个比它小的元素
矩形的左边界是这根柱子左边第一个矮于它的柱子，右边界是这根柱子右边第一个矮于它的柱子

代码实现：

int largestRectangleArea(vector<int>& heights)
 {
        if(heights.empty())
            return 0;
        stack<int> st;
        heights.push_back(0);//为了让最后一个柱子也能够得以处理，在数组末端添加一个高度为0的柱子。
        int res=0;
        for(int i=0;i<heights.size();i++)
        {
            while(!st.empty()&&heights[i]<heights[st.top()])
            {//栈中比当前柱子高的柱子可能不止一个，因此要用while循环
                int curHeight = heights[st.top()];
                st.pop();
                int width = st.empty()? i : i - st.top() - 1;//弹出栈顶元素后栈可能为空，此时矩形的宽度为 i-0=i
                if(width*curHeight>res)
                    res=width*curHeight;
            }
            st.push(i); //单调栈中放的是下标而不是高度
        }
        return res;
    }

具体过程可参照下图：

戳气球

问题描述：

有 $n$ 个气球，编号为 $0$ 到 $n - 1$ ，每个气球上都标有一个数字，这些数字存在数组 nums 中。现在要求你戳破所有的气球。每当你戳破一个气球 $i$ 时，你可以获得 nums[left] * nums[i] * nums[right] 个硬币。这里的 left 和 right 代表和 $i$ 相邻的两个气球的序号。注意当你戳破了气球 i 后，气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。

示例:

输入: [3,1,5,8]
输出: 167 
解释: nums = [3,1,5,8] --> [3,5,8] -->   [3,8]   -->  [8]  --> []
     coins =  3*1*5      +  3*5*8    +  1*3*8      + 1*8*1   = 167

解题思路：

动态规划

状态： $d p [i] [j]$ 表示戳破 $[i, j]$ 范围内这些气球所能获得的最大数量的硬币
转移方程：

 dp[i][j] = max(dp[i][j],dp[i][k-1] + dp[k+1][j] + arr[i-1]*arr[k]*arr[j+1])(i<=k<=j)

方程含义：选择 $i$ 到 $j$ 之间的某一个气球k，然后先戳破 $i$ 到 $k - 1$ 之间的气球，再戳破 $k + 1$ 到 $j$ 之间的气球，最后戳破 $k$ 这个气球。
题目说 $a r r [0]$ 和 $a r r [n + 1]$ 都设置为 $1$ ，所以假如题目给定的气球数目是 $n$ ，那我们的结果就是 $d p [1] [n]$

代码实现：

int maxCoins(vector<int>& nums) 
    {
        int len=nums.size();
        vector<int> vec(len+2);//扩展原始数组
        vec[0]=1;//将第一个置为1
        vec[len+1]=1;//将最后一个置为1
        for(int i=0;i<len;++i)
        {
            vec[i+1]=nums[i];//将原始数组中的数据进行拷贝
        }
     
       vector<vector<int>> dp(len+2,vector<int>(len+2,0));//dp数组
        
        for(int span=1;span<=len;++span)//i-j之间的间隔
        {
            for(int i=1;i<=len-span+1;++i)
            {
                int j=i+span-1;
                for(int k=i;k<=j;++k)//k取[i,j]间的所有数
                {
                    dp[i][j]=max(dp[i][j],dp[i][k-1]+dp[k+1][j]+vec[i-1]*vec[k]*vec[j+1]);   
                }
                
            }
            
            
        }
        return dp[1][len];
                
    }

接雨水

题目描述：
给定 $n$ 个非负整数表示每个宽度为 $1$ 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
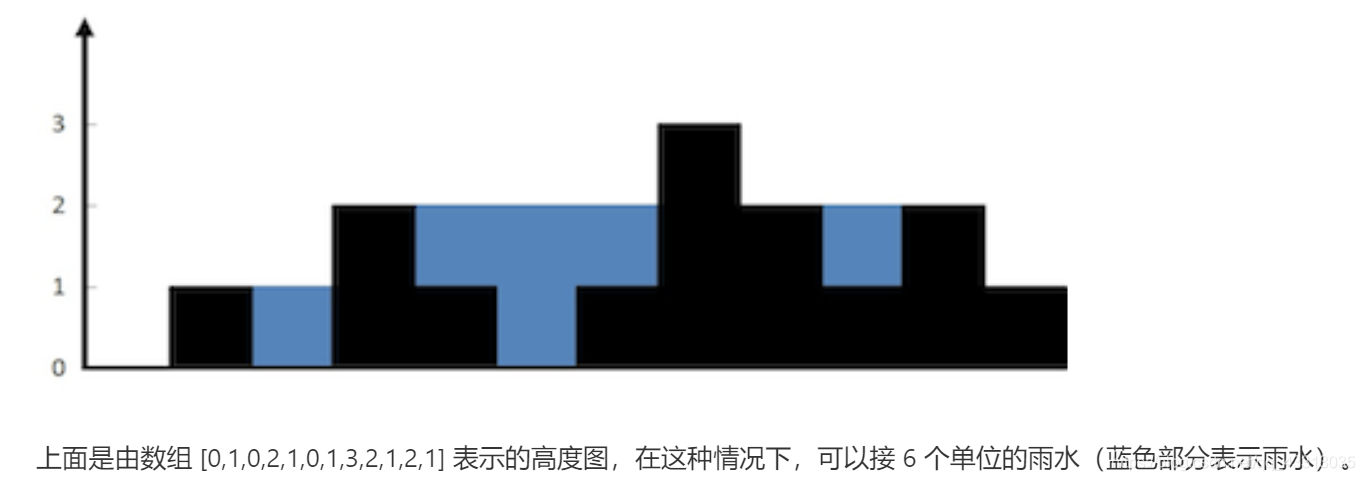
在这里插入图片描述
示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

解题思路：

首先找最高的柱子，记录其下标
找到最高的柱子后，将数组划分两部分
分别从最左边和最右边向最高的柱子靠拢
对于左边来说，如果右边的柱子比左边的柱子低，就可以接雨水
否则就更新左边的高度
对于右边来说，如果右边的柱子比左边的柱子高，就可以接雨水
否则就更新右边柱子的高度

代码实现

int trap(vector<int>& height) 
{
	//首先找最高的柱子，记录其下标和值
    if(height.size()==0)
    {
        return 0;
    }
	int maxval = 0;
	int maxindex = 0;
	for (int i = 0; i < height.size(); ++i)
	{
		if (height[i] > maxval)
		{
			maxval = height[i];
			maxindex = i;
		}
	}
	/*
	找到最高的柱子后，将数组划分两部分
	分别从最左边和最右边向最高的柱子靠拢
	1.对于左边来说，如果右边的柱子比左边的柱子低，就可以接雨水
	  否则就更新左边的高度
	2.对于右边来说，如果右边的柱子比左边的柱子高，就可以接雨水
	  否则就更新右边柱子的高度
	*/
	int leftheight = height[0];
	int rightheight = height[height.size()-1];
	int area = 0;// 表示接的雨水的大小
	for (int i = 0; i < maxindex; ++i)
	{
		if (leftheight < height[i])
		{
			leftheight = height[i];
		}
		else
		{
			area += leftheight - height[i];
		}
	}

	for (int i = height.size() - 1; i >maxindex; --i)
	{
		if (rightheight < height[i])
		{
			rightheight = height[i];
		}
		else
		{
			area += rightheight - height[i];
		}
	}
	return area;
}

字典序的第K小数字

题目描述:
给定整数 $n$ 和 $k$ ，找到 $1$ 到 $n$ 中字典序第 $k$ 小的数字
示例 :

输入:
n: 13   k: 2

输出:
10

解释:
字典序的排列是 [1, 10, 11, 12, 13, 2, 3, 4, 5, 6, 7, 8, 9]，所以第二小的数字是 10。

解题思路：

每个节点的子节点可以有十个，比如节点1的子节点可以是10-19、节点2的子节点可以是20-29…但是由于n大小的限制，构成的并不是一个"满十叉树"。
分析题目中给的例子可以知道，数字1的子节点有4个(10,11,12,13)，而后面的数字2到9都没有子节点，那么这道题实际上就变成了一个先序遍历十叉树的问题。
那么，难点就变成了计算出同一层两个相邻的节点的子节点的个数，也就是代码中的steps
当前节点为 curr （从curr = 1 开始），则同一层的下一个节点为 curr+1;
计算节点 curr到节点curr+1之间的子节点个数steps
如果子节点个数大于 k，说明第k小的树一定在子节点中
继续向下一层寻找：curr=curr*10
k -= 1（原因：向下一层寻找，肯定要减少前面的父节点，即在上一层中的第k个数，在下一层中是第k-1个数）
如果子节点个数小于或者等于 k，说明第k小的树不在子节点中
继续向同一层下一个节点寻找：curr +=1
k -= steps;（原因：向下一层寻找，肯定要减少前面的所有的子节点）
以此类推，直到k为0推出循环，此时cur即为所求。

代码实现：

 int findKthNumber(int n, int k)
  {
        int cur = 1;
        k--;
        
        while (k > 0)
        {
            long long left = cur;
            long long right = cur + 1;
            int node_num = 0;
            
            while (left <= n) // 统计树中每一层的节点个数
            {
                node_num += min(right, (long long)(n+1)) - left;
                left *= 10;
                right *= 10;
            }
            
            if (node_num <= k) // 向后查找
            {
                k -= node_num;
                cur++;
            }
            else // 进入子树查找
            {
                k--;
                cur *= 10;
            }
        }
        
        return cur;       
    }

寻找两个有序数组的中位数

题目描述:

给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。

示例1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0

示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

解题思路：

首先将两个有序数组进行合并
对合并后的数组找中位数

代码实现：

 double findMedianSortedArrays(vector<int>& vec1, vector<int>& vec2) 
    {
        int len1 = vec1.size();
        int len2 = vec2.size();
        int len = len1 + len2;
        int i = 0;
        int j = 0;
        int k = 0;
        vector<int> res(len1+len2);
        while (i < len1&&j < len2)
        {
            if (vec1[i] < vec2[j])
            {
                res[k++]=vec1[i++];
            }
            else
            {
                res[k++] = vec2[j++];
            }
        }
        while (i < len1)
        {
            res[k++] = vec1[i++];
        }
        while (j < len2)
        {
            res[k++] = vec2[j++];
        }
        return (len1 + len2) % 2 == 0 ? (float)(res[len / 2] + res[len / 2 - 1]) / 2 : res[len / 2];
        }

正则表达式匹配

问题描述：

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
所谓匹配，是要涵盖整个字符串s的，而不是部分字符串。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

解题思路：

每次从p中拿出一个字符来与s中的字符进行匹配
如果该字符后续的字符不是 $*$ 那么直接与s中对应字符进行匹配判断即可,，如果匹配上了，那么就将两个游标都往后移动一位。
如果匹配过程中遇到不相等的情况，则直接返回false。
如果后续字符是 $*$ ，那么就如上面所分析的，分成两种情况
一种是匹配0个，那么只需要跳过p中的这两个字符，继续与s中的字符进行比较即可
如果是匹配多个，那么将s中的游标往后移动一个，继续进行判断。这两个条件只要其中一个能满足即可。

代码实现：

bool match(char *s,char *p)
{
    if(*s=='\0'&&*p=='\0')
    {
        return true;
    }
    if(*s!='\0'&&*p=='\0')
    {
        return false;
    }
    
    if(*(p+1)=='*')
    {
        //分三种情况
        //1.第一个字符匹配
        if(*p==*s||*p=='.'&&*s!='\0')
        {
            return match(s+1,p)||match(s,p+2);
        }
        else
        {
            return match(s,p+2);
        }
    }
    else
    {
        if(*s==*p||*p=='.'&&*s!='\0')
        {
            return match(s+1,p+1);
        }
        else
        {
            return false;
        }
    }
}

bool isMatch(char * s, char * p){
    if(s==NULL||p==NULL)
    {
        return false;
    }
    return match(s,p);

}

最长有效括号

问题描述：

给定一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长的包含有效括号的子串的长度。

示例 1:

输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"

示例 2:

输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"

解题思路：
使用动态规划的方法：

$d p [i]$ ：表示以第 $i$ 位为结尾的最长有效括号的长度
存在三种情况
如果 $s [i] = =^{'} (^{'}$ ,直接返回。(因为以左括号结尾，必然不会是有效括号)
$s [i] = =^{'})^{'}$ && $s [i - 1] = =^{'} (^{'}$ ,此时 $d p [i] = d p [i - 2] + 2$
$s [i] = =^{'})$ '&& $s [i - 1] = =^{'})^{'}$ , 此时与该右括号匹配的左括号有可能在 $i - 1$ 之前
需要计算该右括号的对称位置 $(i - 1 - d p [i - 1])$
如果该位置存在且 $s [i - 1 - d p [i - 1]] = =^{'} (^{'}$
则 $s [i] = 2 + d p [i - 2] + d p [i - 2 - d p [i - 1]]$

代码实现：

int longestValidParentheses(string s) 
{
	int len = s.length();
	if (len == 0)
	{
		return 0;
	}
	vector<int> dp(len,0);
	int res = 0;
	for (int i = 1; i < len; ++i)
	{
		if (s[i] == ')')
		{
			if (s[i - 1] == '(')
			{
				dp[i] = 2 + (i - 2 >= 0 ? dp[i - 2] : 0));
			}
			else
			{
				if (i - 1 - dp[i - 1] >= 0 && s[i - 1 - dp[i - 1]] == '(')
				{
					dp[i] = 2 + dp[i - 1] + (i - 2 - dp[i - 1] >= 0 ? dp[i - 2 - dp[i - 1]] : 0);
				}
			}
		}
		res = max(res, dp[i]);
	}
	return res;
}

二叉树中的最大路径和

问题描述：

给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      / \
     2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

解题思路：

最大路径和可能有三种情况 :

在左子树内部
在右子树内部
在穿过左子树，根节点，右子树的一条路径中

设计一个递归函数，返回以该节点为根节点，单向向下走的最大路径和
注意的是，如果这条路径和小于0的话，则置为0，就相当于不要这条路了，要了也是累赘

int left = helper(root->left)
int right = helper(root->right)

我们递归调用这个函数，则最大值为 $l e f t + r i g h t + r o o t - > v a l$ ，我们用一个全局变量不断更新它。
这个递归函数返回的就是 $m a x (l e f t, r i g h t) + r o o t - > v a l$ ，也就是以这个节点为根节点向下走的最大路径和

代码实现：

int maxres = INT_MIN;
    int maxSum(TreeNode *root)
    {
        if (root == nullptr)
        {
            return 0;
        }
        int left = max(0, maxSum(root->left));
        int right = max(0, maxSum(root->right));
        maxres = max(maxres, left + right + root->val);
        return max(left, right) + root->val;
    }
    int maxPathSum(TreeNode* root) {
        maxSum(root);
        return maxres;
    }

串联所有单词的子串

题目描述：

给定一个字符串 $s$ 和一些长度相同的单词 $w o r d s$ 。找出 $s$ 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
注意子串要与 $w o r d s$ 中的单词完全匹配，中间不能有其他字符，但不需要考虑 words 中单词串联的顺序。

示例 1：

输入：
  s = "barfoothefoobarman",
  words = ["foo","bar"]

输出：[0,9]

解释：
从索引 0 和 9 开始的子串分别是 "barfoor" 和 "foobar" 。
输出的顺序不重要, [9,0] 也是有效答案。

示例 2：

输入：
  s = "wordgoodgoodgoodbestword",
  words = ["word","good","best","word"]

输出：[]

解题思路：

首先利用所有的 $w o r d s$ 总长，在 $s$ 串中进行截取一段总长长度的子串
每次在 $s$ 串中从下标 $i$ 开始截取 $w o r d s$ 总长度的子串。
然而对取得的子串进行拆分为 $n$ 个 $w o r d$ ，去匹配 $w o r d s$ 容器中的 $w o r d$

代码实现：

vector<int> findSubstring(string s, vector<string>& words)
    {
        vector<int>  res;
        int len = s.length();//主串的长度
        if (len == 0)
        {
            return {};
        }
        int words_count= words.size();//单词的个数
        if (words_count == 0)
        {
            return {};
        }
        int word_length = words[0].size();//每个单词的长度
        

        //由于题中要求words中的每个单词的长度必须相等
        //因此我们必须对words中每个单词的长度进行判断，如果发现不一致，就直接return
        for (string str : words)
        {
            if (str.size() != word_length)
            {
                return {};
            }
        }

        //首先建立words的映射关系
        unordered_map<string, int> map;
        //遍历words，进行关系的建立
        for (string str : words)
        {
            map[str]++;
        }

        //现在我们开始进行匹配
        //建立滑动窗口，对s串进行遍历
        for (int i = 0; i <= len - words_count * word_length; ++i)
        {
            // 我们需要再建立一个map,用来记录每次匹配的结果
            unordered_map<string, int>   tmpmap = map;
            /*
             用来计算匹配成功的子串的个数
             如果count的值小于words的总个数的时候，就表示此次匹配失败
             如果count的值等于words的个数的时候，表示此次匹配成功
            */
            int count = 0;
            int  j = i;
            while (count< words_count)
            {
                //从j位置截取每个单词长度的子串
                string str = s.substr(j, word_length);
                //如果str不在map中，就直接退出
                if (tmpmap.count(str) == 0 || tmpmap[str] == 0)
                {
                    break;
                }
                tmpmap[str]--;
                j += word_length;
                count += 1;
            }
            //跳出while循环有两种情况
            //1.break调退出
            //2.找完了
            if (count == words_count)
            {
                //表示找到了
                res.push_back(i);
            }
        }
        return res;
    }

恢复二叉搜索树

题目描述：

二叉搜索树中的两个节点被错误地交换。
请在不改变其结构的情况下，恢复这棵树。

示例 1:

输入: [1,3,null,null,2]

   1
  /
 3
  \
   2

输出: [3,1,null,null,2]

   3
  /
 1
  \
   2

示例 2:

输入: [3,1,4,null,null,2]

  3
 / \
1   4
   /
  2

输出: [2,1,4,null,null,3]

  2
 / \
1   4
   /
  3

解题思路：

使用两个容器，其中一个用来存储结点的地址，一个用来存储结点的值
对用来存储结点的值的容器进行排序
排序完之后，将对应的值填写进对应的地址

代码实现：

//根据中序遍历的结果进行节点值和对应地址的存储
void inorder(TreeNode *root, vector<TreeNode *> &str, vector<int> & vec)
{
	if (root == nullptr)
	{
		return;
	}
	inorder(root->left,str,vec);
	str.push_back(root);//存放节点地址
	vec.push_back(root->val);//存放节点的值
	inorder(root->right, str, vec);
	sort(vec.begin(), vec.end());//将节点的值进行排序
	for (int i = 0; i < str.size(); ++i)
	{
		str[i]->val = vec[i];//将排序后的值填写进对应的地址里
	}
}

void recoverTree(TreeNode* root)
{
	if (root == nullptr)
	{
		return;
	}
	vector<TreeNode *> str;//存放每个结点的值
	vector<int> vec;//存放对应地址的值
	inorder(root, str, vec);
}

二叉树中的最大路径和

题目描述：

给定一个非空二叉树，返回其最大路径和。
本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      / \
     2   3

输出: 6

示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

解题思路：

在递归函数中，如果当前结点不存在，那么直接返回0。
否则就分别对其左右子节点调用递归函数，由于路径和有可能为负数，而我们当然不希望加上负的路径和，所以我们和0相比，取较大的那个，就是要么不加，加就要加正数。
然后我们来更新全局最大值结果 maxres，就是以左子结点为终点的最大path之和加上以右子结点为终点的最大path之和，还要加上当前结点值，这样就组成了一个条完整的路径。

代码实现：

int maxres = INT_MIN;
    int maxSum(TreeNode *root)
    {
        if (root == nullptr)
        {
            return 0;
        }
        int left = max(0, maxSum(root->left));
        int right = max(0, maxSum(root->right));
        maxres = max(maxres, left + right + root->val);
        return max(left, right) + root->val;
    }
    int maxPathSum(TreeNode* root) {
        maxSum(root);
        return maxres;

    }