PTA 哈夫曼编码 (30 分)

最新推荐文章于 2023-12-06 19:04:11 发布

原创

最新推荐文章于 2023-12-06 19:04:11 发布 · 3.2k 阅读

16 ·

CC 4.0 BY-SA版权

博客介绍了如何判断哈夫曼编码的正确性，通过对比编码长度和最优编码长度，以及检查是否存在公共前缀来确定。作者分享了解题思路，包括避免建立哈夫曼树的复杂方法，转而使用结构体和数组来优化求解过程。

PTA 哈夫曼编码 (30 分)

有一段时间没写博客了，不能停止更新，发几个数据结构练习题的题解

哈夫曼编码

给定一段文字，如果我们统计出字母出现的频率，是可以根据哈夫曼算法给出一套编码，使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz"，容易得到字母’a’、‘x’、‘u’、‘z’ 的出现频率对应为 4、2、1、1。我们可以设计编码 {‘a’=0, ‘x’=10, ‘u’=110,‘z’=111}，也可以用另一套 {‘a’=1, ‘x’=01, ‘u’=001, ‘z’=000}，还可以用 {‘a’=0,‘x’=11, ‘u’=100, ‘z’=101}，三套编码都可以把原文压缩到 14 个字节。但是 {‘a’=0, ‘x’=01,‘u’=011, ‘z’=001}就不是哈夫曼编码，因为用这套编码压缩得到 00001011001001后，解码的结果不唯一，“aaaxuaxz” 和 "aazuaxax"都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。

输入格式：

首先第一行给出一个正整数 N（2≤N≤63），随后第二行给出 N 个不重复的字符及其出现频率，格式如下：
c[1] f[1] c[2] f[2] … c[N] f[N]
其中c[i]是集合{‘0’ - ‘9’, ‘a’ - ‘z’, ‘A’ - ‘Z’, ‘_’}中的字符；f[i]是c[i]的出现频率，为不超过 1000 的整数。再下一行给出一个正整数 M（≤1000），随后是 M 套待检的编码。每套编码占 N 行，格式为：
c[i] code[i]
其中c[i]是第i个字符；code[i]是不超过63个’0’和’1’的非空字符串。

输出格式：

对每套待检编码，如果是正确的哈夫曼编码，就在一行中输出"Yes"，否则输出"No"。
注意：最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。

输入样例：

7
A 1 B 1 C 1 D 3 E 3 F 6 G 6
4
A 00000
B 00001
C 0001
D 001
E 01
F 10
G 11
A 01010
B 01011
C 0100
D 011
E 10
F 11
G 00
A 000
B 001
C 010
D 011
E 100
F 101
G 110
A 00000
B 00001
C 0001
D 001
E 00
F 10
G 11

输出样例：

Yes
Yes
No
No

这道题当时准备建立一个哈哈哈哈哈夫曼树进行求解，但是想到代码量就放弃了，因为身为ACMer我~~太懒了~~ 要追求更好的解题策略！

代码写了100行左右（加上注释就多了），我大概搜了搜其他人的基本上都是150+。。。

解题思路：

这道题主要有两个部分，首先要求解出WPL最优编码长度，和给定的编码的总长度进行对比，如果给出的不是最优的直接结束。第二步是判断给出的编码有没有公共前缀，没有公共前缀才是合格的哈哈哈哈哈夫曼编码。

第一部分求解WPL暴力的方法（建树）会浪费很大的空间和时间，我用了一个结构体List模拟一个子树，我没有保留树的结构，而是用list储存一个子树的叶节点（即要编码的字符），用一个变量储存子树根节点的权值（叶节点权值之和），然后模拟建哈哈哈哈哈夫曼树的过程，过程中不断更新每一个字符的深度（用数组保存）。

下面就是模拟过程（随缘画法），每一行是循环一次后优先队列的内容，一个红圈是一个子树（结构体List，数字是根节点的权值）

建树过程

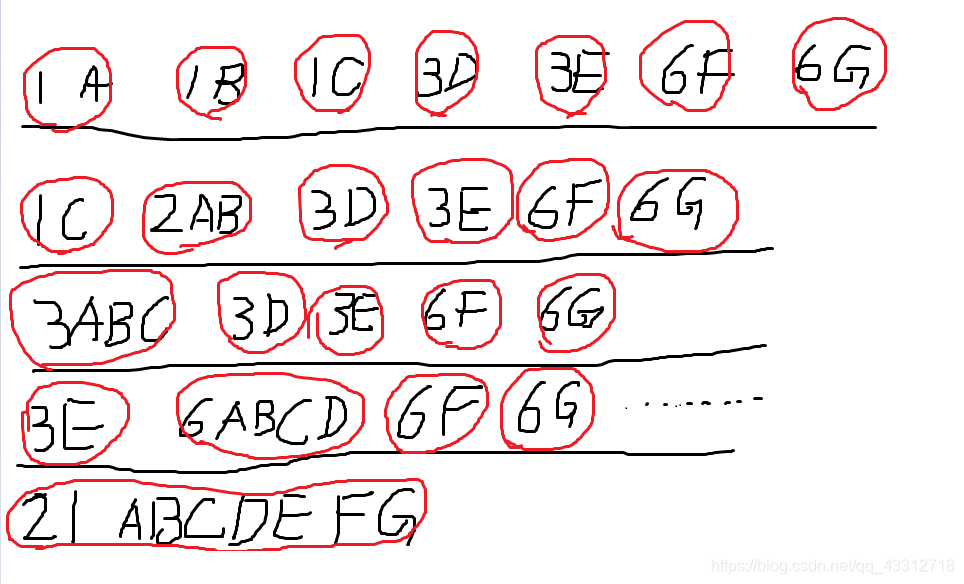
#include <algorithm>
#include <iostream>
#include <string>
#include <queue>
#include <list>
using namespace std;

struct List//这是一个子树
{
   
   
    list<char> l;//储存子树的叶节点（即编码的字符）
    int p;//子树祖先节点的权值（等于所有叶节点编码长度之和）
    bool operator <(<