《论文阅读》Accurate and Robust Scale Recovery for Monocular Visual Odometry Based on Plane Geometry-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43310834/article/details/119295051

留个笔记自用

Accurate and Robust Scale Recovery for Monocular Visual Odometry Based on Plane Geometry

做什么

Monocular Visual Odometry单目视觉里程计
在这里插入图片描述
相机在运动过程中连续两帧之间会存在overlap，即会同时观测到三维世界中的某些场景以及特征点。而这些场景特征点会投射到2D图片上，通过图片的对齐或者特征的匹配，可以找到前后图片上特点或patch的对应关系。利用相机的成像几何模型（包括相机参数）以及约束，可以求出两帧之间的运动信息（旋转矩阵R和平移t）。这样我们就可以得到一系列的相机相对变化矩阵，从而可以推出相机的姿态信息。

做了什么

在这里插入图片描述
这里构造了一个轻量级框架，能实现对地面的精确稳健的估计，框架包括用于在地平面上选择高质量点的地面点提取算法，以及用于在局部滑动窗口中连接提取的地面点的地面点聚集算法，主要优点就是能提取出高质量的地面点。

怎么做

首先仍然是问题定义和符号定义
在这里插入图片描述为第t帧的SO(3)，由旋转矩阵R_t∈R^3×3和平移向量T_t∈R³组成
为第t-1至t的相对位姿转换，也就是前面的SO(3)的相对版
K表示相机的内有矩阵
x_i表示相机帧上的3D点，u_i表示相机帧投影到平面上的2D点
h，h+，h分别为由图像特征估计的摄像机高度，由尺度恢复得到的摄像机高度，真实的摄像机高度
任务描述：输入是一个连续的图像帧，目标是估计相机的相对位姿转换，然后通过相机高度h还原轨迹，也就是说，任务目标就是得到摄像机高度h+
由于这里是单目相机，最重要的就是恢复图像内的尺度信息，也就是2D不具备的深度信息
在这里插入图片描述
整个框架由两个部分组成，第一部分是MVO部分，输入连续图像，估计当前的相机位姿转换，这里使用了一些现有框架来进行，如ORB-SLAM2框架。第二部分是尺度恢复部分，使用GPE和GPA等算法。
简单来说，主要步骤是通过第一部分输出相机位姿转换，这是一个初始化值，第二部分通过这个位姿转换和算法得到的尺度来进行位姿修复。
在图中也有步骤的分解
在这里插入图片描述
绿框内就是MVO部分，初始化一个位姿转换
主要是后面的红框和橙框，两者组成了第二部分尺度恢复部分

首先是红框部分，对于当前的图像帧，用Delaunay Triangulate（三角剖分法）这个方法将匹配的特征点分割成一系列三角形
在这里插入图片描述
然后将这些三角形反投影到相机框架中，来寻找地面点
然后是橙框部分

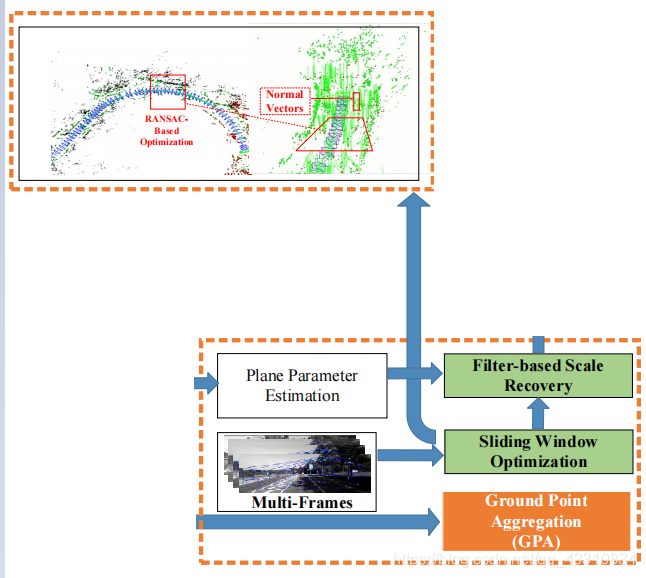
用滑动窗口和GPA来聚集局部地面点，这两个框的具体在后面会解释
然后就是具体细节的实现部分
首先是地面点估计，也就是红框部分的实现，GPE
在这里插入图片描述
输入是匹配的特征点u_i^t，就是对于当前t帧图像帧，用三角剖分法将每个特征点作为顶点建立三角形，然后反投影到图像帧上
定义反投影的顶点为x_ij^t，每个三角形的法向量为

满足
这是常见的几何约束，也就是说对于每个反投影点x存在的三角形都有这么一个约束，用法向量可以将点全部约束到一个维度上，简单来说就是可以估算这个i三角形的高度h
除此之外还添加了两个约束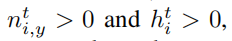，在这里插入图片描述
这里的理解就是三角形的高度是大于地面的，因为摄像头是安装在车之上的
这样整个图像帧会存在多个三角形，而这里需要的仅仅是地面三角形，因为这些是用来估计地面参数地面点的

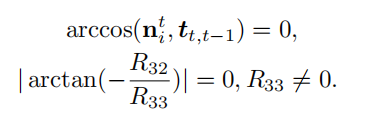
这里的意思就是，对于地面三角形的法向量，它应该是和相机位姿转换中的平移向量t是垂直的，这个很好理解，然后是下面那个，这里的意思是摄像机的俯仰角应该为0，这个是因为摄像机是在平移的车上进行移动的，高度不会产生变化，这就是两个地面三角形估计的约束
对于满足上述约束的三角形，就可以视为地面三角形在这里插入图片描述
而地面三角形的顶点x，就被视为地面点
然后再把被多个三角形共享的重复点去掉成单独点，除此之外还要消除一些移动平面物体的混淆点之类的，这里用了RANSAC的方法最小化平面函数

这个优化公式的意思就是最小化地面点和相机的高度差
在这里插入图片描述
GPE的整体流程是这样的，相当复杂啊，大致理解一下过程，第一步三角形化匹配特征点，第二步将特征点反投影到图像帧，然后计算三角形法向量和高度之类的东西，这里有用到前面说的一些几何约束，第三步就是获取地面点，方法就是优化那个最小化函数，然后强化一下这些点，随机选3个点，组一个平面，计算剩余点到平面的距离，重复Z次保留最小距离的点
然后是地面点聚合，也就是橙框部分的实现，GPA
在这里插入图片描述
GPA的作用就是在连续帧中聚合地面点，这是对前面初步得到的地面点的一种细化吧可以说是，首先这里的连续图像帧是通过滑动窗口得到的，其实就是选局部序列输入
从前一个部分MVO部分和红框部分中可以得到初始化的位姿转换T_t和每帧的内联点x_g^t也就是地面点
然后就可以将每个内联点转换到全局帧框架上
在这里插入图片描述
然后构造了一个缓冲区，当前窗口中的一些信息比如地面点位姿转换之类的都存着，每个时间步长随着新图像帧来了就更新缓冲区，用最小二乘法更新估计地平面

这里的N是缓冲区的局部地面点数，这里的意思是最小化这些点的平面距离差，其中大P是这N个点的p_i组成的
将这个式子改写一下
在这里插入图片描述

然后就可以用SVD进行优化了
最终就可以得到全局平面，有了这个平面就可以计算相机相对高度了

p_c是I_t帧的相机中心
至此，通过GPA就能得到一个全局的平面，通过这个平面计算得到了相对的相机高度h，这个h就是最前面的问题定义中所需要的
在这里插入图片描述
这里也相当复杂，简单看一下，其实就是使用最小二乘法更新局部缓冲区得到的平面，这个平面是由前面部分的地面点聚合得到的

最后的最后是蓝框部分，尺度恢复部分

通过前面计算得到了每帧的摄像机相对高度h+，然后就可以对轨迹进行一个尺度恢复
在这里插入图片描述
这里的s_t是比例因子
这里的h*是真实高度，然后就可以通过这个比例因子对平移t进行尺度缩放