Python学习笔记，主成分分析法

主成分分析

整理整理自己学习python过程中的知识点，主成分分析法。
首先为什么需要主成分分析呢？比方说：记得高一时，一到期末就会有八门课的考试，而这八门课的成绩对你的成绩排名影响比重是不一样的。语文不怎么拉得开分，而数学的话对排名的影响还是比较大的。从这里面可以看出，八个特征值对你最终排名的贡献率是不一样的。这里我们就需要用到主成分分析法。将数据进行降维来分析，避免一些无用功。

接下来介绍一下主成分分析的步骤：
1.先求均值，再减去均值
2.计算协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.特征值从小到大排序，保留K个最大特征值
5.将mn的数据集乘以k个n维的特征向量的特征向量（nk），得到降维数据

值得注意的是为什么特征值 要从大到小排？
之前说了每一门课的重要程度是不一样的，而特征值越大，样本就越离散，信息量就越多，越容易区分，他就越重要。

接下来是使用sklearn库中的PCA分析iris数据集（鸢尾花卉数据集）
以下是代码：

import matplotlib.pyplot as pyl
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

#导入鸢尾花数据，系统自带的数据
data = load_iris()
#提取出两组数据
y = data.target
x = data.data
#加载PCA算法
pca = PCA()
#训练数据
pca.fit(x)
#计算模型中各个特征量
tzl = pca.components_
print("各个特征量为：")
print(tzl)
#计算各个成分中各方差的百分比，贡献率
bfz = pca.explained_variance_ratio_
print("各贡献率为：")
print(bfz)


#确定要降的维数
pca1 = PCA(2)
#训练数据
pca1.fit(x)
#降维
pca_x = pca1.transform(x)

#提取类别
yellow_x,yellow_y = [],[]
red_x,red_y = [],[]
green_x,green_y = [],[]

for i in range(0,len(pca_x)):
    if y[i] == 0:
        yellow_x.append(pca_x[i][0])
        yellow_y.append(pca_x[i][1])
    if y[i] == 1:
        red_x.append(pca_x[i][0])
        red_y.append(pca_x[i][1])
    if y[i] == 2:
        green_x.append(pca_x[i][0])
        green_y.append(pca_x[i][1])
#可视化
pyl.plot(yellow_x,yellow_y,'y*')
pyl.plot(red_x,red_y,'rd')
pyl.plot(green_x,green_y,'g.')
pyl.savefig("D:/python/数据分析算法/主成分分析/iris.png")
pyl.show()

其中0,1,2分别代表的是鸢尾花的类别：setosa, versicolor, virginica

以下是得到的分析图：

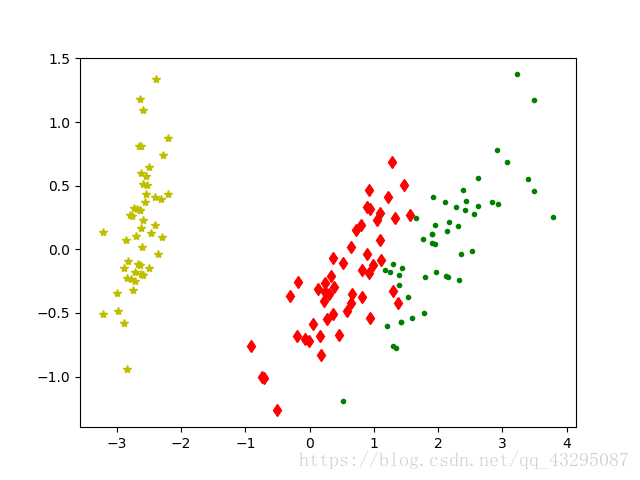
可以看到图中数据还是清楚的分为三类。