文章目录
论文原文
摘要
基于会话的推荐(SBR)侧重于某一时间点的下一项预测。由于在这种情况下用户概要文件通常不可用,因此捕获项目转换中的用户意图发挥了关键作用。
现有的基于图神经网络(GNNs)的SBR方法将项目转换视为成对关系,忽略了项目之间复杂的高阶信息。超图提供了一种捕获超成对关系的自然方法,而它在SBR中的潜力还未被开发。
在本文中,我们通过将基于会话的数据建模为超图来填补这一空白,然后提出一个双通道超图卷积网络- DHCN来改进SBR。此外,为了增强超图建模,我们创新地将自监督学习集成到网络的训练中,最大化DHCN中通过两个通道学习到的会话表示之间的相互信息,作为辅助任务来改进推荐任务。在三个基准数据集上的大量实验证明了我们的模型优于SOTA方法,消融研究验证了超图建模和自监督任务的有效性和基本原理。
介绍
基于会话的推荐(SBR)是一种新兴的推荐范式,其中长期用户资料通常不可用。通常,会话是一个购物事件中包含多个购买商品的事务,SBR通过使用实时用户行为关注下一个商品的预测。在这一领域的大多数研究工作将会话视为有序序列,其中基于循环神经网络(RNNs) 和基于图神经网络(GNNs) 的方法显示了良好的性能。
在基于RNNs的方法中,将基于会话的数据建模为单向序列被认为是成功的关键,因为数据通常在短时间内生成,而且很可能是时间依赖性的。然而,这种假设也可能会使这些基于rnn的模型陷入困境,因为它是欠考虑的。事实上,不像语言序列是按照严格的顺序生成的,在用户行为中,可能没有这样严格的时间顺序。例如,在Spotify上,用户可以选择打乱一张专辑或按顺序播放,这将生成两种不同的收听记录。然而,这两种播放模式都序列化同一组歌曲。换句话说,在这种情况下,颠倒两个项目的顺序不会导致用户偏好的扭曲。相反,如果只对项目的相对顺序进行严格建模,可能会使推荐模型容易过拟合。
过拟合(over-fitting)也称为过学习,它的直观表现是算法在训练集上表现好,但在测试集上表现不好,泛化性能差。过拟合是在模型参数拟合过程中由于训练数据包含抽样误差,在训练时复杂的模型将抽样误差也进行了拟合导致的。所谓抽样误差,是指抽样得到的样本集和整体数据集之间的偏差。直观来看,引起过拟合的可能原因有:
- 模型本身过于复杂,以至于拟合了训练样本集中的噪声。此时需要选用更简单的模型,或者对模型进行裁剪。
- 训练样本太少或者缺乏代表性。此时需要增加样本数,或者增加样本的多样性。
- 训练样本噪声的干扰,导致模型拟合了这些噪声,这时需要剔除噪声数据或者改用对噪声不敏感的模型。
最近,图神经网络(GNNs)的有效性已在包括SBR在内的许多领域报道。与基于rnns的推荐方法不同,基于gnns的方法将基于会话的数据建模为有向子图,将项目转换建模为成对关系,这略微放松了连续项目之间的时间依赖性假设。然而,与基于rnn的方法相比,现有的模型只显示出微不足道的改进。潜在的原因是他们忽略了基于会话的数据中复杂的项相关性。在实际场景中,项目转换通常是由以前的项目单击的联合作用触发的,项目之间存在多对多和高阶关系。显然,简单的图无法描述这种类似集合的关系。
为了克服这些问题,我们提出了一种新的基于超图的SBR方法,以模拟会话中项目之间的高阶关系。
从概念上讲,超图(Bretto 2013)由顶点集和超边集组成,其中超边可以连接任意数量的顶点,可用于编码高阶数据相关性。我们还假设会话中的项目在时间上是相关的,但不是严格的顺序依赖的。超边的特征完全符合我们的假设,因为超边是类似的,它强调所涉及元素的连贯性而不是相对顺序。因此,它为我们提供了在会话中捕获复杂交互的灵活性和能力。
从技术上讲,我们首先将每个会话建模为一个超边,其中所有项都相互连接,通过共享项连接的不同超边构成了包含项级高阶相关性的超图。然后,通过将每个超边建模为一个节点,基于该超图构建线图,并关注超边的连通性,从而描述会话级关系。之后,开发了一个双通道超图卷积网络(DHCN),分别从两个图中获取其两个通道的复杂项目相关性和交叉会话信息。
图1说明了超图构造和所提出方法的流水线。通过在两个通道中堆叠多层,我们可以借用超图卷积的优势来生成高质量的推荐结果。然而,由于每个超边只包含有限数量的项,固有的数据稀疏性问题可能会限制超图建模带来的好处。为了解决这个问题,我们创新性地将自我监督学习(Hjelm等人,2018年)集成到我们的模型中,以增强超图建模。直观地说,我们网络中的两个通道可以被看作是描述会话内部和内部信息的两个不同视图,而它们中的每一个对另一个的信息知之甚少。通过自监督学习使通过两个通道学习的会话表示之间的互信息最大化,两个通道可以相互获取新信息,以提高它们在项目/会话特征提取中的性能。然后,我们将推荐任务和自我监督任务统一在主辅助学习框架下。通过联合优化这两个任务,推荐任务的性能获得了可观的收益。
总体而言,这项工作的主要贡献总结如下:
- 我们提出了一种用于SBR的双通道超图卷积网络,该网络可以通过超图建模来捕捉项目之间的跨空中关系和跨会话信息。
- 我们创新地将自我监督任务集成到我们的网络训练中,以增强超图建模并改进推荐任务。
- 大量实验表明,我们提出的模型比最先进的基线具有压倒性优势,并在基准数据集上取得了显著的统计改进。
相关工作
基于会话的推荐SBR
SBR的初步探索主要集中于序列建模,其中马尔可夫决策过程是该阶段的首选技术。(Shani、Heckerman和Brafman 2005年;Rendle、Freudenthaler和Schmidt-Thieme 2010年;Zimdars、Chickering和Meek 2013年)是这一研究领域的代表性作品。深度学习的繁荣提供了利用顺序数据的替代方法。诸如递归神经网络(Hochreiter和Schmidhuber 1997;Cho等人2014)和卷积神经网络(Tuan和Phuong 2017)等深度学习模型随后被应用于SBR并取得了巨大成功。(Hidasi等人2015年;Tan、Xu和Liu 2016年;Li等人2017年;Liu等人2018年)是经典的基于RNN的模型,它借用了RNN的优势来建模基于会话的数据。
图形神经网络(GNN)(Wu等人,2020年;Zhou等人,2018年)最近引起了越来越多的关注,其在SBR中的应用也显示出了良好的结果(Wang等人,2020b,c;Y uan等人,2019年;Chen和Wong 2020年)。与处理顺序数据的基于RNN的方法不同,基于GNN的方法通过会话诱导图学习项目转换。SR-GNN(Wu等人2019b)是一项开创性工作,它使用门控图神经网络将会话建模为图结构数据。GC-SAN(Xu等人,2019年)采用自我注意机制,通过图形信息聚合捕获项目依赖性。FGNN(邱等,2019)构建会话图来学习项目转换模式,并重新思考SBR中项目的顺序。GCE-GNN(Wang等人2020c)对单个会话图和全局会话图进行图卷积,以学习会话级和全局级嵌入。尽管这些研究表明,基于GNN的模型优于其他方法,包括基于RNN的模型,但它们都未能捕捉到复杂的高阶项目相关性。
超图学习
超图为复杂的高阶关系提供了一种自然的方式。随着深度学习的兴起,超图神经网络也受到了广泛的关注。HGNN(Feng等人2019)和HyperGCN(Y adati等人2019年)是第一个将图卷积应用于超图的。(Jiang et al 2019)提出了一种动态超图神经网络,(Bandyopadhyay,Das和Murty 2020)开发了线超图卷积网络。
还有一些研究将超图学习与推荐系统相结合(Bu等人2010;Li和Li 2013)。与我们最相关的工作是HyperRec(Wang等人,2020a),它使用超图来模拟用户对下一项推荐的短期偏好。但是,它不利用超边缘间信息,也不设计用于基于会话的场景。此外,该模型的高度复杂性使得它不可能在实际场景中部署。目前,还没有研究将超图神经网络和SBR连接起来,我们是第一个填补这一空白的人。
自我监督学习
自监督学习(Hjelm等人,2018)是一种新兴的机器学习范式,旨在从原始数据中学习数据表示。它首先用于视觉表征学习(Bachman、Hjelm和Buchwalter 2019)。该领域的最新进展将自监督学习扩展到图形表示学习(Velickovic等人,2019年)。基于对比学习的主导范式(Hassani和Khasahmadi 2020;Qiu等人,2020a)表明,对比具有相互信息最大化的图的一致和不一致视图可以帮助编码丰富的图/节点表示。
由于自我监督学习仍处于初级阶段,只有几项研究将其与推荐系统相结合(Zhou等人2020;Ma等人2020;Xin等人2020)。与我们最相关的工作是S3 Rec(Zhou等人,2020年),用于顺序推荐,它使用特征掩码创建自我监控信号。但它不适用于SBR,因为会话数据非常稀疏。目前,超图表示学习和SBR的自监督学习潜力尚未得到研究。我们是第一个将自我监督学习集成到SBR和超图建模场景中的人。
具体实现方法
在本节中,我们首先介绍本文中使用的概念和定义,然后展示如何将基于会话的数据建模为超图。然后,我们给出了SBR的双通道超图卷积网络。最后,我们将自监督学习集成到网络中以增强超图建模。
符号和定义
设
I
=
{
i
1
,
i
2
,
i
3
,
…
,
i
n
}
I = \{i_1,i_2,i_3,\ldots,i_n\}
I={i1,i2,i3,…,in}表示项的集合,其中N是项的数目
每个会话表示为集合
s
=
[
i
s
,
1
,
i
s
,
2
,
i
s
,
3
,
…
,
i
s
,
m
]
s=[i_{s,1},i_{s,2},i_{s,3},\ldots,i_{s,m}]
s=[is,1,is,2,is,3,…,is,m]其中
i
s
,
k
∈
(
1
≤
k
≤
m
)
i_{s,k} \in (1\leq k\leq m)
is,k∈(1≤k≤m) 表示会话s中匿名用户的交互项s.
我们嵌入每个项目
i
∈
I
i \in I
i∈I进入同一空间,设
x
i
(
l
)
∈
R
d
(
l
)
x_i^{(l)}\in\Reals^{d^{(l)}}
xi(l)∈Rd(l) 表示深度神经网络的第
i
i
i层中维度
d
(
l
)
d^{(l)}
d(l)的项目
i
i
i的向量表示。
整个项目集的表示表示为
X
(
l
)
∈
R
N
×
d
(
l
)
X^{(l)}\in\Reals^{N\times d^{(l)}}
X(l)∈RN×d(l)。每个会话s由向量
s
⃗
\vec{s}
s表示。SBR的任务是预测任何给定会话s的下一项,即
i
s
,
m
+
1
i_{s,m+1}
is,m+1。
定义1,超图
设
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)表示超图,其中
V
V
V是包含
N
N
N个唯一顶点的集合,
E
E
E是包含
M
M
M个超边的集合。
每个超边
ϵ
∈
E
\epsilon\in E
ϵ∈E包含两个或多个顶点,并被赋予正权重
W
ϵ
ϵ
W_{\epsilon\epsilon}
Wϵϵ,并且所有权重形成对角矩阵
W
∈
R
M
×
M
W \in \Reals^{M \times M}
W∈RM×M。
超图可以用关联矩阵
H
∈
R
N
×
M
H \in \Reals^{N \times M}
H∈RN×M表示,其中如果是超边
ϵ
∈
E
\epsilon \in E
ϵ∈E包含顶点
v
i
∈
V
v_i \in V
vi∈V,
H
i
ϵ
=
1
H_{i\epsilon}=1
Hiϵ=1,否则为0。
对于每个顶点和超边,它们的度数
D
i
i
D_{ii}
Dii和
B
e
e
B_{ee}
Bee
分别定义为
D
i
i
=
∑
ϵ
=
1
M
W
ϵ
ϵ
H
i
ϵ
D_{ii} =\sum_{\epsilon=1}^{M} {W_{\epsilon\epsilon}H_{i\epsilon}}
Dii=∑ϵ=1MWϵϵHiϵ;
B
ϵ
ϵ
=
∑
i
=
1
N
H
i
ϵ
B_{\epsilon\epsilon} =\sum_{i=1}^{N} {H_{i\epsilon}}
Bϵϵ=∑i=1NHiϵ其中
B
{\bf {B}}
B是对角矩阵。
定义2:超图的线图
给定超图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E) ,线图
L
(
G
)
L(G)
L(G)是这样的一个图,线图
L
(
G
)
L(G)
L(G)的每个节点都是超图
G
G
G中的一个超边,并且线图
L
(
G
)
L(G)
L(G)中的两个节点是相连的如果他们对应的在超图
G
G
G中对应的超边至少含有一个相同的点。
形式上,
L
(
G
)
=
(
V
L
,
E
L
)
L(G)=(V_L,E_L)
L(G)=(VL,EL) ,其中
V
L
=
{
v
e
:
v
e
∈
E
}
V_L = \{v_e:v_e \in E\}
VL={ve:ve∈E},并且
E
L
=
{
(
v
e
p
,
v
e
q
)
:
e
p
,
e
q
∈
E
,
∣
e
p
∩
e
q
∣
≥
1
}
E_L = \{(v_{e_p},v_{e_q}):e_p,e_q \in E,|e_p \cap e_q| \geq 1\}
EL={(vep,veq):ep,eq∈E,∣ep∩eq∣≥1} .
我们为每条边
(
v
e
p
,
v
e
q
)
(v_{e_p},v_{e_q})
(vep,veq) 指定一个权重
W
p
,
q
W_{p,q}
Wp,q 其中
W
(
p
,
q
)
=
∣
e
p
∩
e
q
∣
/
∣
e
p
∪
e
q
∣
W_(p,q) = |e_p \cap e_q| / |e_p \cup e_q|
W(p,q)=∣ep∩eq∣/∣ep∪eq∣
超图的构造
为了捕捉基于会话的推荐中的超配对关系,我们采用超图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)将每个会话表示为超边。
形式上,我们将每个超边表示为
[
i
s
,
1
,
i
s
,
2
,
i
s
,
3
,
…
,
i
s
,
m
]
∈
E
[i_{s,1},i_{s,2},i_{s,3},\ldots,i_{s,m}] \in E
[is,1,is,2,is,3,…,is,m]∈E,每项表示为
i
s
,
m
∈
V
i_{s,m} \in V
is,m∈V
超图构建前后数据结构的变化如图1左侧所示。如图所示,原始会话数据被组织为线性序列,其中两项
i
s
,
m
−
1
,
i
s
,
m
i_{s,m-1},i_{s,m}
is,m−1,is,m 为仅当与项目交互的用户为
i
s
,
m
−
1
i_{s,m-1}
is,m−1 时才连接−项目之前的
i
s
,
m
i_{s,m}
is,m 。
将会话数据转换为超图后,会话中单击的任何两个项目都将连接起来。应该注意的是,我们将会话序列转换为无向图,这符合我们的直觉,即会话中的项目是时间相关的,而不是顺序相关的。通过这样做,我们设法将多对多高阶关系具体化。此外,我们根据定义2进一步归纳了超图的线图。每个会话被建模为一个节点,并且不同的会话通过共享项连接。与描述项目级高阶关系的超图相比,线图描述了也称为跨会话信息的会话级关系。

双通道超图卷积网络
在构建超图之后,我们开发了一个双通道超图卷积网络DHCN,以捕获项目级高阶关系和会话级关系。网络中的每个信道负责从一个(超)图中提取有用信息,以通过(超)卷积来改善SBR。
超图通道和卷积
超图通道对超图进行编码。由于有两个通道,直接馈送完整的基本项嵌入
X
(
0
)
∈
R
N
×
d
X^{(0)} \in \Reals^{N \times d}
X(0)∈RN×d到两个信道是不明智的。为了控制流向每个通道的嵌入量,我们使用了带有自选通单元(SGU)的预滤波器,其定义如下:
X
C
(
0
)
=
f
g
a
t
e
c
(
X
(
0
)
)
=
X
(
0
)
⊙
σ
(
X
(
0
)
W
g
c
+
b
g
c
)
(1)
X_{C}^{(0)}=f_{gate}^{c}(X^{(0)})=X^{(0)} \odot \sigma(X^{(0)}W_{g}^{c}+b_{g}^{c}) \tag{1}
XC(0)=fgatec(X(0))=X(0)⊙σ(X(0)Wgc+bgc)(1)
其中
W
g
c
∈
R
d
×
d
W_{g}^{c} \in \Reals^{d \times d}
Wgc∈Rd×d,
b
g
c
∈
R
d
b_{g}^{c} \in \Reals ^d
bgc∈Rd是要学习的选通参数,
c
∈
{
h
,
l
}
c \in \{h,l\}
c∈{h,l}表示通道,
⊙
\odot
⊙表示逐元素乘积,
σ
\sigma
σ是sigmod函数。
自门控机制通过维度重加权以特征粒度调制基本项嵌入,然后我们获得超图通道特定项的嵌入
X
h
(
0
)
X_{h}^{(0)}
Xh(0)
在超图上定义卷积运算的主要挑战是如何传播项的嵌入。参考(Feng等人2019)中提出的谱超图卷积,我们将超图卷曲定义为:
x
i
l
+
1
=
∑
j
=
1
N
∑
ϵ
=
1
M
H
i
ϵ
H
j
ϵ
W
ϵ
ϵ
x
j
(
l
)
p
(
l
)
(2)
x_{i}^{l+1}=\sum_{j=1}^{N} {\sum_{\epsilon=1}^{M} {H_{i\epsilon}H_{j\epsilon}W_{\epsilon\epsilon}x_{j}^{(l)}p^{(l)}}} \tag{2}
xil+1=j=1∑Nϵ=1∑MHiϵHjϵWϵϵxj(l)p(l)(2)
其中
P
(
l
)
∈
R
d
×
d
{\bf {P}}^{(l)} \in \Reals^{d \times d}
P(l)∈Rd×d是两个卷积层之间的可学习参数矩阵。根据(Wu等人2019a)中的建议,我们不使用非线性激活函数。对于
W
ϵ
ϵ
W_{\epsilon\epsilon}
Wϵϵ,我们给每个超边分配相同的权重1。
具有行归一化的公式
(
1
)
(1)
(1)的矩阵形式为:
X
h
(
l
+
1
)
=
D
−
1
H
W
B
−
1
H
T
X
h
(
l
)
P
(
l
)
(3)
{\bf {X}}_{h}^{(l+1)} = {\bf{D^{-1}}}{\bf {HWB^{-1}}}{\bf {H}}^{T}{\bf {X}}_h^{(l)}{\bf {P}}^{(l)} \tag{3}
Xh(l+1)=D−1HWB−1HTXh(l)P(l)(3)
超图卷积可以看作是对超图结构进行“节点-超边-节点”特征变换的两阶段细化。乘法运算
H
T
X
h
(
l
)
{\bf {H}}^{T}{\bf {X}}_h^{(l)}
HTXh(l)定义了从节点到超边的信息聚合,然后将预乘
H
{\bf{H}}
H视为从超边到节点的信息聚合。
在将
X
h
(
0
)
X_{h}^{(0)}
Xh(0)通过
L
L
L超图卷积层之后,我们将在每个层获得的项目嵌入平均,以获得最终的项目嵌入
X
h
∗
=
1
L
+
1
∑
l
=
0
L
X
h
(
l
)
{\bf {X}}_{h}^{*} = \frac {1}{L+1}\sum_{l=0}^{L}{{\bf{X}}_{h}^{(l)}}
Xh∗=L+11∑l=0LXh(l)。会话嵌入可以通过聚合该会话中的项目表示来表示。我们遵循SR-GNN(Wu等人2019b)中使用的策略来细化会话
s
=
[
i
s
,
1
,
i
s
,
2
,
i
s
,
3
,
…
,
i
s
,
m
]
s=[i_{s,1},i_{s,2},i_{s,3},\ldots,i_{s,m}]
s=[is,1,is,2,is,3,…,is,m]的嵌入:
α
t
=
f
⊤
σ
(
W
1
x
m
∗
+
W
2
x
t
∗
+
c
)
,
s
g
=
∑
t
=
1
m
α
t
x
t
∗
,
θ
h
=
W
3
[
x
m
∗
;
s
g
]
,
(4)
\begin{aligned} \alpha_t &=\mathbf{f}^{\top} \sigma\left(\mathbf{W}_1 \mathbf{x}_m^*+\mathbf{W}_2 \mathbf{x}_t^*+\mathbf{c}\right), \\ \mathbf{s}_g &=\sum_{t=1}^m \alpha_t \mathbf{x}_t^*, \quad \theta_h=\mathbf{W}_3\left[\mathbf{x}_m^* ; \mathbf{s}_g\right], \end{aligned} \tag{4}
αtsg=f⊤σ(W1xm∗+W2xt∗+c),=t=1∑mαtxt∗,θh=W3[xm∗;sg],(4)
其中
x
m
∗
\mathbf{x}_m^*
xm∗是会话s中最后一项的嵌入,
x
t
∗
\mathbf{x}_t^*
xt∗会话s中第t项的嵌入
让
x
m
∗
\mathbf{x}_m^*
xm∗表示当前用户意图,以及用户在该会话中的一般兴趣嵌入
s
g
s_g
sg通过软关注机制聚合项目嵌入来表示,其中项目具有不同的优先级。
f
∈
R
d
f\in\Reals^d
f∈Rd,
W
1
∈
R
d
×
d
W_1\in\Reals^{d \times d}
W1∈Rd×d和
W
2
∈
R
d
×
d
W_2\in\Reals^{d \times d}
W2∈Rd×d是用于学习物品重量
α
t
\alpha_t
αt的注意力参数。
混合会话嵌入
θ
h
\theta_h
θh连
x
m
∗
x_m^*
xm∗和
s
g
s_g
sg表示从超图结构和W3推断出的完整用户偏好,
W
3
∈
R
d
×
2
d
W_3\in\Reals^{d \times 2d}
W3∈Rd×2d将混合会话嵌入到
R
d
\Reals^d
Rd空间中。注意,根据第一节中的动机,我们放弃了其他SBR模型中使用的序列建模技术,如GRU单元和自我关注。当前的意图是我们使用的唯一时间因素,因此我们的模型非常高效和轻量级。
线图通道和卷积
线形图通道对超图的线形图进行编码。图1显示了我们如何将超图转换为它的线图。线图可以看作是一个简单的图,它包含跨会话信息并描述了超边的连通性。类似地,在卷积运算之前,我们通过SGU传递
X
(
0
)
X^{(0)}
X(0)以获得线条图通道特定项嵌入
X
l
(
0
)
X_l^{(0)}
Xl(0)。由于线形图通道中没有涉及项目,我们首先通过查找属于每个会话的项目,然后对
X
l
(
0
)
X_l^{(0)}
Xl(0)中的相应项目进行平均,来初始化特定于通道的会话嵌入
Θ
l
(
0
)
\Theta_l^{(0)}
Θl(0)。
L
(
G
)
L(G)
L(G)的关联矩阵定义为
A
∈
R
M
×
M
A \in \Reals^{M \times M}
A∈RM×M,其中
M
M
M是线图中的节点数并且
A
p
,
q
=
W
p
,
q
A_{p,q} = W_{p,q}
Ap,q=Wp,q根据定义2。设
A
^
=
A
+
I
\hat{A} = A + I
A^=A+I,其中
I
I
I是单位矩阵。
D
^
∈
R
M
×
M
\hat{{\mathbf{D}}} \in \Reals ^{M \times M}
D^∈RM×M是对角度矩阵,其中
D
^
=
∑
q
=
1
m
A
^
p
,
q
\hat{{\mathbf{D}}}=\sum_{q=1}^{m}{\hat{{A}}_{p,q}}
D^=∑q=1mA^p,q。线图卷积定义为:
Θ
l
(
l
+
1
)
=
D
^
−
1
A
^
Θ
(
l
)
Q
(
l
)
(5)
\boldsymbol{\Theta}_l^{(l+1)}=\hat{\mathbf{D}}^{-1} \hat{\mathbf{A}} \Theta^{(l)} \mathbf{Q}^{(l)} \tag{5}
Θl(l+1)=D^−1A^Θ(l)Q(l)(5)
其中
Q
(
l
)
∈
R
d
×
d
\mathbf{Q}^{(l)} \in \Reals^{d \times d}
Q(l)∈Rd×d是权重矩阵。在每个卷积中,会话从其邻居收集信息。通过这样做,学习的
Θ
\boldsymbol{\Theta}
Θ可以捕获跨会话信息。同样地,我们通过
L
L
L图卷积层传递
Θ
l
(
0
)
\boldsymbol{\Theta}_l^{(0)}
Θl(0),然后对在每个层获得的会话嵌入求平均,以获得最终会话嵌入
Θ
l
=
1
L
+
1
∑
l
=
0
L
Θ
l
(
l
)
\boldsymbol{{\Theta}_l}=\frac{1}{L+1}\sum_{l=0}^{L}{\boldsymbol{\Theta}_l^{(l)}}
Θl=L+11∑l=0LΘl(l)。
模型优化和推荐生成
给定一个会话s,我们通过分别在基本项嵌入
X
0
X^0
X0和
θ
s
h
\theta_s^h
θsh和
θ
s
l
\theta_s^l
θsl之间进行内积计算所有候选项
i
∈
I
i \in I
i∈I的得分
z
^
\hat{\bf{z}}
z^。然后我们将两个预测分数相加,得到最终预测:
z
^
i
=
(
θ
s
h
+
θ
s
l
)
T
x
i
.
(6)
\hat{\mathbf{z}}_i=\left(\theta_s^h+\theta_s^l\right)^T \mathbf{x}_i . \tag{6}
z^i=(θsh+θsl)Txi.(6)
之后,应用softmax函数计算会话中每个项目成为下一个项目的概率:
y
^
=
s
o
f
t
m
a
x
(
z
^
)
(7)
\hat{\mathbf{y}}=softmax(\hat{\mathbf{z}}) \tag{7}
y^=softmax(z^)(7)
我们将学习目标表述为交叉熵损失函数,该函数已广泛应用于推荐系统中,并定义为:
L
r
=
−
∑
i
=
1
N
y
i
log
(
y
^
i
)
+
(
1
−
y
i
)
log
(
1
−
y
^
i
)
(8)
\mathcal{L}_r=-\sum_{i=1}^N \mathbf{y}_i \log \left(\hat{\mathbf{y}}_i\right)+\left(1-\mathbf{y}_i\right) \log \left(1-\hat{\mathbf{y}}_i\right) \tag{8}
Lr=−i=1∑Nyilog(y^i)+(1−yi)log(1−y^i)(8)
其中
y
\mathbf{y}
y是标准答案(ground truth)的一个热编码矢量。为了简单起见,我们省略了
L
2
L_2
L2正则化项。通过使用Adam最小化
L
r
L_r
Lr,我们可以获得高质量的基于会话的推荐。
通过自我监督学习增强DHCN
超图建模使我们的模型能够实现显著的性能。然而,我们认为会话数据的稀疏性可能会阻碍超图建模,这将导致次优推荐性能。受简单图上的自监督学习成功实践的启发,我们创新地将自监督学习集成到网络中,以增强超图建模。使用自我监督信号学习被视为有益于我们推荐任务的辅助任务,它通过以下两个步骤进行:
- 创建自我监督信号。回想一下,在DHCN中,我们通过两个通道学习了两组特定于通道的会话嵌入。由于每个信道编码一个(超)图,该图只描述了会话诱导超图的项目级(会话内)或会话级(会话间)结构信息,因此两组嵌入彼此了解甚少,但可以相互补充。对于训练中包含n个会话的每个迷你批处理,两组会话嵌入之间有一个双射映射。直截了当地说,这两组人可以成为自我监督学习的基础,这种一对一的映射被视为标签的增加。如果两个会话嵌入都表示两个视图中的同一个会话,我们将这一对标记为基本真理,否则我们将其标记为否定。
- 对比学习。继V elickovic等人2019年;Bachman、Hjelm和Buchwalter 2019年)之后,我们将DHCN中的两个频道视为表征会话不同方面的两种观点。然后,我们将通过这两个视图学习的两组会话嵌入进行对比。我们采用InfoNCE(Oord、Li和Vinyals 2018)作为学习目标,将基础真值(正)样本和损坏样本(负)样本之间的标准二进制交叉熵损失定义为:
L s = − log σ ( f D ( θ i h , θ i l ) ) − log σ ( 1 − f D ( θ ~ i h , θ i l ) ) , (9) \mathcal{L}_s=-\log \sigma\left(f_{\mathrm{D}}\left(\theta_i^h, \theta_i^l\right)\right)-\log \sigma\left(1-f_{\mathrm{D}}\left(\tilde{\theta}_i^h, \theta_i^l\right)\right), \tag{9} Ls=−logσ(fD(θih,θil))−logσ(1−fD(θ~ih,θil)),(9)
式中 θ ~ i h ( o r θ ~ i i ) \tilde{\theta}_i^h(or\tilde{\theta}_i^i) θ~ih(orθ~ii)是通过逐行和逐列混洗 Θ h ( Θ l ) \boldsymbol{{\Theta}_h}(\boldsymbol{{\Theta}_l}) Θh(Θl)获得的负样本, f D ( ⋅ ) : R d × R d ↦ R f_D(\cdot):\Reals^d \times \Reals^d \mapsto \Reals fD(⋅):Rd×Rd↦R是鉴别器函数,它将两个向量作为输入,然后对它们之间的一致性进行评分。我们简单地将鉴别器实现为两个矢量之间的点积。该学习目标被解释为最大化在不同视图中学习的会话嵌入之间的相互信息(V elickovic等人2019)。通过这样做,他们可以相互获取信息,以通过卷积运算提高自己在项目/会话特征提取中的性能。特别是,那些只包含少数项目的会话可以利用跨会话信息来优化其嵌入。
最后,我们将推荐任务和自我监督任务统一为一个主辅助学习框架,前者是主任务,后者是辅助任务。形式上,联合学习目标定义为:
L = L r + β L s , (10) \mathcal{L}=\mathcal{L}_r+\beta \mathcal{L}_s, \tag{10} L=Lr+βLs,(10)
其中 β \beta β控制自我监督任务的大小。
实验
实验设置
数据集
我们在两个真实世界基准数据集上评估我们的模型:Yoochoose和Diginetica。对于这两个数据集,我们遵循(Wu等人2019b;Li等人2017),删除只包含一个项目的所有会话,并删除出现少于五次的项目。为了评估我们的模型,我们按照(Wu等人2019b;Li等人2017)中的设置,将两个数据集分成训练/测试集。
对于Yoochoose数据集,测试集由与训练集相关的随后几天的会话组成。
对于Diginetica数据集,唯一的区别是我们使用随后几周的会话进行测试。
然后,对于每个会话
s
=
[
i
s
,
1
,
i
s
,
2
,
…
,
i
s
,
m
]
s=[i_{s,1},i_{s,2},\ldots,i_{s,m}]
s=[is,1,is,2,…,is,m],我们通过使用序列分裂方法来扩展和标记数据集,该方法生成多个标记序列,并带有相应的标记
(
[
i
s
,
1
]
,
i
s
,
2
)
,
(
[
i
s
,
1
,
i
s
,
2
]
,
i
s
,
3
)
,
…
,
(
[
i
s
,
1
,
i
s
,
2
,
…
,
i
s
,
m
−
1
]
,
i
s
,
m
)
([i_{s,1}],i_{s,2}),([i_{s,1},i_{s,2}],i_{s,3}),\ldots,([i_{s,1},i_{s,2},\ldots,i_{s,m-1}],i_{s,m})
([is,1],is,2),([is,1,is,2],is,3),…,([is,1,is,2,…,is,m−1],is,m)请注意,每个序列的标签是其中最后一个单击项。由于Yoochoose的训练集相当大,我们遵循(Wu等人2019b;刘等人2018;Li等人(2017年)只利用最新的1/64和1/4的整个训练序列,并为我们的实验形成两个新的训练集,并将它们命名为Yoochoose1/64和Yoochoose1/4。数据集的统计数据如表1所示
基线方法(Baseline Methods)
我们将DHCN与以下代表性方法进行比较:
- Item-KNN:推荐与会话中先前单击的项目类似的项目,其中使用会话向量之间的余弦相似性。
- FPMC:是一种基于马尔可夫链的顺序方法。
- NARM:是基于RNN的模型,其对顺序行为建模以生成推荐。
- STAMP:采用自我关注机制来增强基于会话的推荐。
- SR-GNN:应用门控图卷积层来学习项目转换。
- FGNN :将会话内的下一项建议公式化为图分类问题。
评估指标
跟随(Wu等人2019b;Liu等人2018),我们使用P@K(精度)和MRR@K(平均倒数排名)来评估推荐结果。
超参数设置
对于一般设置,嵌入大小为100,小批量的批量大小为100并且 L 2 L_2 L2正则化为 1 0 − 5 10^{-5} 10−5.对于DHCN,采用两层结构,并使用初始学习率0.001。对于基线模型,我们参考原始论文中报告的最佳参数设置,并直接报告其结果(如果可用),因为我们使用相同的数据集和评估设置。
实验结果
总体性能
表2中报告了总体性能的实验结果,我们用黑体突出显示了每一列的最佳结果。对DHCN的两个变体进行了评估,
S
2
−
D
H
C
N
(
β
=
3
)
S^2-\bf {DHCN}(\beta=3)
S2−DHCN(β=3)表示自监督版本。
通过使用
S
2
−
D
H
C
N
S^2-DHCN
S2−DHCN的性能与最佳基线之间的差异来划分后者的性能来计算改进。由于在Yoochoose1/4上运行
F
P
M
C
FPMC
FPMC的内存需求对于普通深度学习计算平台来说太大,因此我们不报告类似FPMC的结果(Li等人,2017年)。通过分析表2中的结果,我们可以得出以下结论。

- 基于GNN的模型:SR-GNN和FGNN优于基于RNN的模型。这些改进可以归功于图形神经网络的巨大容量。然而,与DHCN带来的改进相比,这些改进也微不足道。
- 我们提出的DHCN在所有数据集的所有基线上显示出压倒性优势。特别是,Diginetica的改进是显著的。在分析Diginetica的数据模式后,我们发现许多项目经常以频繁项目集的形式出现在不同的会话中,这是超图建模的理想选择。这可能是导致如此非凡结果的原因。与SR-GNN和FGNN相比,我们的模型有两个优点:
- 它使用超图来捕捉超配对关系。通过将每个超边建模为项目完全连接的集团,可以利用远处项目之间的连接。
- 线形图考虑了跨会话信息。此外,值得注意的是,MRR方面的改进比Precision方面的改进更为显著,这意味着DHCN不仅能够成功地触及实际情况,而且在很大程度上提升了其在前K名推荐列表中的排名。
- 尽管没有超图建模带来的效果那么显著,但自监督学习带来的改进仍然不错。特别是,在会话平均长度较短的两个数据集上,自监督学习起着更重要的作用,这与我们的假设一致,即会话数据的稀疏性可能会妨碍超图建模的好处,而最大化DHCN中两个视图之间的互信息可以解决这一问题。
Ablation Study消融实验
消融实验:设立对照组的意思,通过去除某个模块的作用,来证明该模块的必要性,如果消融实验后得到结果不好或者性能大幅下降,说明该模块起到了作用。
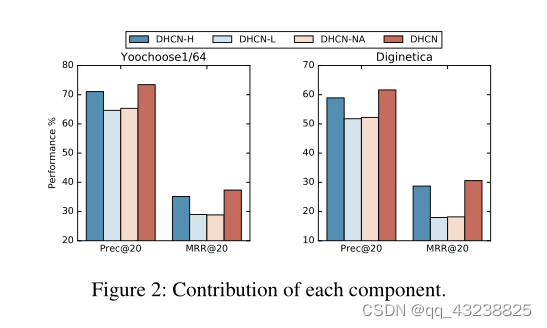
在最后一节中显示的DHCN的压倒性优势可以看作是超图建模和时间因素开发的联合作用的结果。为了研究DHCN中每个模块的贡献,我们开发了DHCN的三个变体:DHCN-H、DHCN-L和DHCN-NA。DHCN-H表示只使用超图通道,DHCN-L表示只采用线形图通道。DHCN-NA代表版本没有软注意机制。我们将其与Yoochoose1/64和Diginetica上的完整DHCN进行比较。
如图2所示,每个组件都有助于最终的性能。超图通道贡献最大。当仅使用此信道(注意使用)时,网络的性能显著高于两个数据集上基线的性能。相比之下,仅使用线形图通道将导致两个数据集的性能大幅下降。但在数字上,DHCN-L仍然与基线相当。这可以证明建模高阶项目相关性的有效性,以及捕获跨会话信息以补充项目级信息的必要性。此外,移除超图通道中的软注意力也会导致两个数据集的性能大幅下降,这与我们在第一节中的假设一致,即会话中的项目在时间上是相关的。根据这项消融研究,我们可以得出结论,一个成功的SBR模型应该同时考虑时间因素和高阶项目相关性。
不同会话长度的影响
在现实世界中,会话通常有不同的长度。在处理这些问题时,有必要了解DHCN的稳定性。我们遵循(Liu等人,2018年)将Yoochoose1/64和Diginetica分为两组,每组长度不同,并将其命名为
s
h
o
r
t
\bf{short}
short和
l
o
n
g
\bf{long}
long。
s
h
o
r
t
\bf{short}
short包含长度小于或等于5的会话,而
l
o
n
g
\bf{long}
long包含长度大于5的会话。我们选择切割点为5,因为它是所有会话中最常见的长度。然后,我们依据P@20的
s
h
o
r
t
\bf{short}
short和
l
o
n
g
\bf{long}
long比较了DHCN和NARM、STAMP和SR-GNN。图3中的结果显示,在大多数情况下,DHCN在不同会话长度的Yoochoose1/64和Diginetica上稳定地优于所有基线模型。特别是,
l
o
n
g
\bf{long}
long的表现比基线要好得多。结果证明了DHCN在基于会话的真实世界推荐中的适应性。
模型深度的影响
为了研究DHCN深度的影响,我们将DHCN的层数范围定为{1,2,3,4}。根据图4所示的结果,DHCN对两个数据集上的层数不是很敏感。双层设置是最好的。当层数大于2时,由于过度平滑,性能略有下降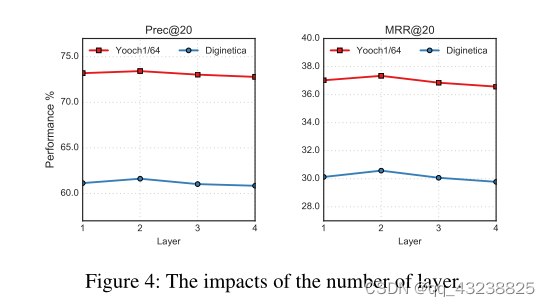
自我监督学习的影响
我们将超参数 β \beta β引入到 s 2 − D H C N s^2-DHCN s2−DHCN以控制自监督学习的幅度。研究基于双视角对比学习的自我监督任务的影响。我们报告了一组具有代表性的 β \beta β值 { 0.1 、 1 、 3 、 5 、 10 、 20 、 50 } {0.1、1、3、5、10、20、50} {0.1、1、3、5、10、20、50}的 s 2 − D H C N s^2-DHCN s2−DHCN的性能。根据图5所示的结果,当使用自我监督任务进行优化时,推荐任务可以获得可观的收益。小 β \beta β可以促进两者Prec@20和MRR@20在两个数据集上。然而,随着 β \beta β的增加,MRR@下降,而Prec@20目前,我们不知道为什么没有性能下降Prec@20,希望在我们未来的工作中找到答案。总的来说,这意味着在选择 β \beta β值时,在命中率和物品等级之间进行权衡是很重要的。

结论
现有的基于GNN的SBR模型将项目转换视为成对关系,无法捕捉项目之间普遍存在的高阶相关性。本文提出了一种用于SBR的双通道超图卷积网络来解决这一问题。此外,为了进一步增强网络性能,我们创新性地将自监督集成到网络的训练中。大量的实证研究证明了我们模型的压倒性优势,消融研究验证了超图卷积和自我监督学习的有效性和合理性。
阅读总结

embedding
one-hot
超图构建前后数据结构的变化如图1左侧所示。如图所示,原始会话数据被组织为线性序列,其中两项
i
s
,
m
−
1
,
i
s
,
m
i_{s,m-1},i_{s,m}
is,m−1,is,m 为仅当与项目交互的用户为
i
s
,
m
−
1
i_{s,m-1}
is,m−1 时才连接−项目之前的
i
s
,
m
i_{s,m}
is,m 。
将会话数据转换为超图后,会话中单击的任何两个项目都将连接起来。应该注意的是,我们将会话序列转换为无向图,这符合我们的直觉,即会话中的项目是时间相关的,而不是顺序相关的。通过这样做,我们设法将多对多高阶关系具体化。此外,我们根据定义2进一步归纳了超图的线图。每个会话被建模为一个节点,并且不同的会话通过共享项连接。与描述项目级高阶关系的超图相比,线图描述了也称为跨会话信息的会话级关系.
在构建超图之后,我们开发了一个双通道超图卷积网络DHCN,以捕获项目级高阶关系和会话级关系。网络中的每个信道负责从一个(超)图中提取有用信息,以通过(超)卷积来改善SBR。
整个超图的构造和提出的DHCN模型的流水线过程如上图所示:
- 构造超图
- 由超图变为线图和将会话中单击的任何两个项目连起来得到新的超图
- 超图进入超图超通道卷积网络,线图进入线图通道和卷积网络
- 经过softmax组件构成推荐的生成
自我监督学习的方法:
- 创建自我监督信号。回想一下,在DHCN中,我们通过两个通道学习了两组特定于通道的会话嵌入。由于每个信道编码一个(超)图,该图只描述了会话诱导超图的项目级(会话内)或会话级(会话间)结构信息,因此两组嵌入彼此了解甚少,但可以相互补充。对于训练中包含n个会话的每个迷你批处理,两组会话嵌入之间有一个双射映射。直截了当地说,这两组人可以成为自我监督学习的基础,这种一对一的映射被视为标签的增加。如果两个会话嵌入都表示两个视图中的同一个会话,我们将这一对标记为基本真理,否则我们将其标记为否定。
- 对比学习。继V elickovic等人2019年;Bachman、Hjelm和Buchwalter 2019年)之后,我们将DHCN中的两个频道视为表征会话不同方面的两种观点。然后,我们将通过这两个视图学习的两组会话嵌入进行对比。我们采用InfoNCE(Oord、Li和Vinyals 2018)作为学习目标,将基础真值(正)样本和损坏样本(负)样本之间的标准二进制交叉熵损失定义为:
L s = − log σ ( f D ( θ i h , θ i l ) ) − log σ ( 1 − f D ( θ ~ i h , θ i l ) ) , (9) \mathcal{L}_s=-\log \sigma\left(f_{\mathrm{D}}\left(\theta_i^h, \theta_i^l\right)\right)-\log \sigma\left(1-f_{\mathrm{D}}\left(\tilde{\theta}_i^h, \theta_i^l\right)\right), \tag{9} Ls=−logσ(fD(θih,θil))−logσ(1−fD(θ~ih,θil)),(9)
式中 θ ~ i h ( o r θ ~ i i ) \tilde{\theta}_i^h(or\tilde{\theta}_i^i) θ~ih(orθ~ii)是通过逐行和逐列混洗 Θ h ( Θ l ) \boldsymbol{{\Theta}_h}(\boldsymbol{{\Theta}_l}) Θh(Θl)获得的负样本, f D ( ⋅ ) : R d × R d ↦ R f_D(\cdot):\Reals^d \times \Reals^d \mapsto \Reals fD(⋅):Rd×Rd↦R是鉴别器函数,它将两个向量作为输入,然后对它们之间的一致性进行评分。我们简单地将鉴别器实现为两个矢量之间的点积。该学习目标被解释为最大化在不同视图中学习的会话嵌入之间的相互信息(V elickovic等人2019)。通过这样做,他们可以相互获取信息,以通过卷积运算提高自己在项目/会话特征提取中的性能。特别是,那些只包含少数项目的会话可以利用跨会话信息来优化其嵌入。
最后,我们将推荐任务和自我监督任务统一为一个主辅助学习框架,前者是主任务,后者是辅助任务。形式上,联合学习目标定义为:
L = L r + β L s , (10) \mathcal{L}=\mathcal{L}_r+\beta \mathcal{L}_s, \tag{10} L=Lr+βLs,(10)
其中 β \beta β控制自我监督任务的大小。























 1851
1851

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








