2021-06-27数据结构与算法基础-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43199016/article/details/118273394

1. 数据结构

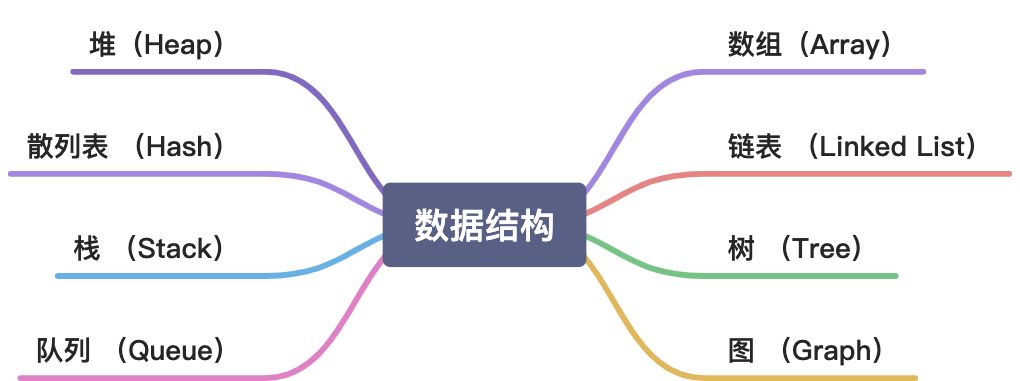
1.1 数据结构是什么？

数据结构是计算机存储、组织数据的一种方式。数据结构是指相互存在一种或多种特定关系的数据元素集合、进行选择的数据结构可以带来更高的程序运行或存储效率。数据结构与高效的检索算法和索引技术有关。

1.2 常见的数据结构有哪些？

**数组（Array）：**数组是最基本的数据结构，它是将具有相同类型的若干变量有序的组织在一起。

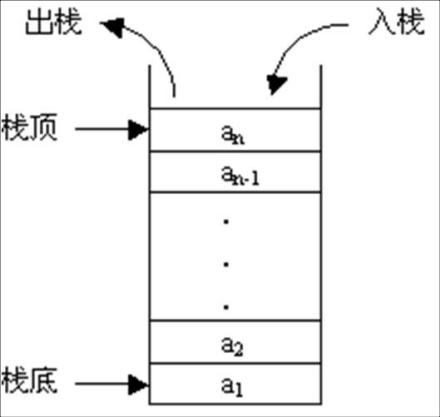
**栈（Stack）：**栈是一种特殊的线性表，它只能在一个固定的端点进行数据节点的插入和删除操作。栈按照先进先出的原则来存储数据。也就是说先插入的数据将被压入栈底，最后插入的数据在栈顶，读取数据时从栈顶逐个读取。

**队列（Queue）：**队列也是一种线性表，和栈不同的是队列只允许在表的一端进行插入操作，而在另一端进行删除操作。一般来说进行插入操作的一端叫做队尾，进行删除操作的一端称为队头。

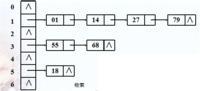
链表（Linked List）：链表是物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表的指针链接次序实现的。链表的么个节点都会包含两个部分一个是数据元素的数据域，一个是存储下一个节点的指针域。

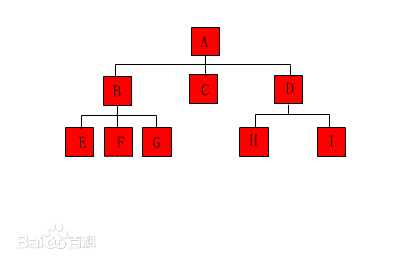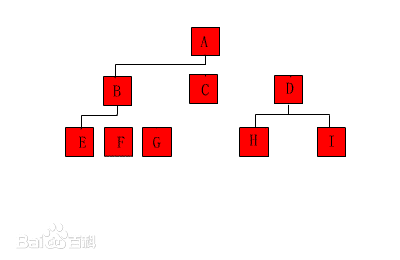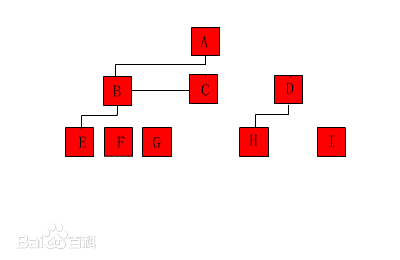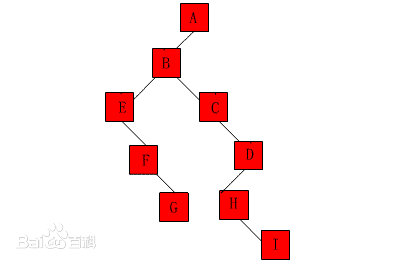
树（Tree）：树是一种非线性结构，它是包括，2个节点的有穷集合K。在树结构中，有且仅有一个根节点，该节点没有前驱节点。在树结构中的其他节点都有且仅有一个额前驱节点，而且可以有两个后继节点，m≥0。

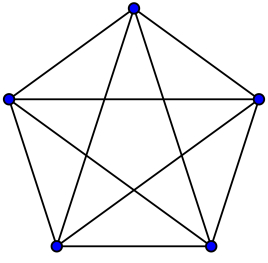
图（Graph）：图也是一种非线性结构。在图结构中，数据结点一般被称为顶点，而边是顶点的有序偶对。如果两个顶点之间存在一条边，那么就表示这两个顶点具有相邻关系。

堆（Heap）：堆是一种特殊的树形数据结构，一般讨论推都是二叉堆。堆的特点是根节点的值是所有结点中最小的或者最大的，并且根结点的两个子树也是一个堆结构。
散列表（Hash）：散列表源自于散列函数，其中心思想是如果在结构中存在关键字和T相等的记录，那么必定在F(T)的存储位置可以找到该记录，这样就可以不用进行比较操作而直接去的所查记录。

2. 算法

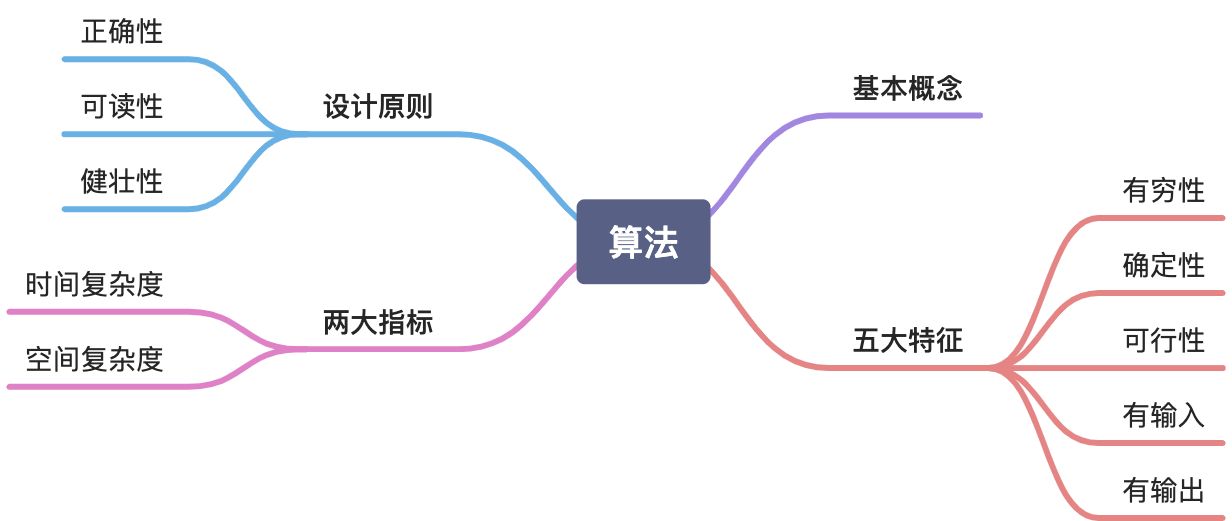
2.1 算法的基本概念

算法是用于解决实际问题的一段程序代码，它有输入、输出并且具有确定性、有穷性和可行性

2.2 算法的五大特征

有穷性：是可以被执行完成的，具有有限的执行次数。
确定性：算法的执行范围是可以确定的。
可行性：是可以解决实际问题的。
有输入：可以有输入的条件。
有输出：可以产生运行结果，没有结果的运行时没有意义的。

2.3 算法的设计原则

正确性：可以解决实际问题。
可读性：算法程序代码能够快速被其他人看懂。
健壮性：很少bug，程序代码运行稳定。

2.4 算法的两大指标

2.4.1 时间复杂度

基本概念

在算法中，时间复杂度用O表示，常见的时间复杂度有O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(nn)，时间复杂度指的是运行一段程序所需要花费的时间。

计算时间复杂度往往是计算比较大的，而且是不确定的数，如果已经确定了，那就不用计算了，也就是我们说的常量。

O后面的括号中是一个函数，指明某个算法耗时与数据增长量之间的关系其中n代表输入数据的量

O(1)

O(1)表示是常数阶，所有能够被确定的执行次数都可以用O(1)表示，它是最低的空间复杂度，也是就是耗时与输入数据大小无关，无论输入数量增大多少倍，耗时都不变。哈希算法就是典型的O(1)时间复杂度，无论数据规模多大，都可以在一次计算后找到结果（在不考虑冲突的情况下）。

public class HelloWorld{
    
    public static void main(String[]args){
    
        //时间复杂度 O(1)
        System.out.println("Hello World!!!");
    
        //时间复杂度 O(1)
        for(int i = 0;i<=100;i++){
           // ..... 省略逻辑
        }
       
    }
    
}

O(logn)

O(logn)表示对数阶，当数据量增大n倍时，耗时增大logn倍（这里的log是以2为敌，比如当数据量增大256倍时，耗时只增加8被，比线性还要低的时间复杂度）

public class HelloWorld{

    public static void main(){
        
        //时间复杂度 O(logn)
        int n = 100;
        while(n > 1){
            n = n * 2;
        }
    }
    
}

O(n)

O(n)表示线性阶，表示数据量增大几倍，耗时量也得增大几倍

public class HelloWorld{

    public static void main(){
        
        //时间复杂度 O(n)
        int n = 未知大小;
        for(int i = 0;i<=n;i++){
           // ..... 省略逻辑
        }
        
    }
    
}

O(nlogn)

O(nlogn)表示线性对数阶，就是n乘以logn，当数据增大256倍时，耗时增大256*8=2048倍，这个复杂度高于线性低于平方

public class HelloWorld{

    public static void main(){
        
        //时间复杂度 O(n)
        int n = 未知大小;
        for(int i = 0;i<=n;i++){
           // ..... 省略逻辑
            while(n > 1){
                n = n * 2;
            }
        }
        
    }
    
}

O(n^2)

O(n^{2)表示平方阶，当数据增大n倍时，耗时增大n}2倍

public class HelloWorld{

    public static void main(){
        
        //冒泡排序 时间复杂度 O(n^2)
        int[]arr = new arr[5]{{0,5,1,3,2}};
        
        for(int i = 0;i < arr.length - 1;i++){
            for(int j = i;j<arr.length - 1 - i;j++){
                int tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
            }
        }
    }
    
}