天勤2022数据结构（三）串

最新推荐文章于 2021-08-17 09:42:24 发布
最新推荐文章于 2021-08-17 09:42:24 发布
阅读量580 收藏 6
点赞数 1
分类专栏： 考研 数据结构 文章标签： 算法 字符串 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_43130927/article/details/115270889
版权

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

前言

定长顺序存储
typedef struct{
	char str[maxSize+1];
	int length;
}Str;

变长分配存储
typedef struct{
	char* ch;
	int length;
}Str;

基本操作

赋值

int strcpy(Str& str, char* ch){
	if(str.ch){
		free(str.ch);
	}
	int len = 0;
	char* c = ch;
	while(*c){
		len++;
		c++;
	}
	if(len == 0){
		str.ch = NULL;
		str.length = 0;
		return 1;
	}
	str.ch = (char*)malloc(sizeof(char)*(len+1));
	if(str.ch == NULL)	//malloc失败
		return 0;
	c = ch;
	for(int i = 0; i<=len; i++){
		str.ch[i] = c;
		c++;
	}
	str.length = len;
	return 1;
}

取长度

int strlen(Str str){
	return str.length;
}

比较

int strcmp(Str s1, Str s2){
	for(int i = 0; i<s1.length && i<s2.length; i++){
		if(s1.str[i] != s1.str[j){
			return s1.str[i] - s2.str[i];
		}
	}
	return s1.length - s2.length;
}

拼接

int strcat(Str &str, Str s1, Str s2){
	if(str.ch){
		free(str.ch);
		str.ch = NULL;
	}
	str.ch = (char*)malloc(sizeof(char)*(s1.length + s2.length + 1));
	if(str,ch == NULL){
		return 0;
	}
	int i = 0;
	while(i<s1.length){
		str.ch[i] = s1.ch[i];
		i++;
	}
	int j = 0;
	while(j<=s2.length){	// <= 复制最后'\0'
		str.ch[i+j] = s1.ch[j];
		j++;
	}
	str.length = s1.length + s2.length;
	return 1;
}

求子串

int substring(Str &substr, Str str, int pos, int len){
	if(pos < 0 || pos > str.length || len < 0 || len >str.length){
		return 0;
	}
	if(substr.ch){
		free(substr.ch);
		substr.ch = NULL;
	}
	if(len == 0){
		substr.ch = NULL;
		substr.length = 0;
		return 1;
	}
	substr.ch = (char*)malloc(sizeof(char) * (len+1));
	int i = pos, j = 0;
	while(j<len){
		substr.ch[j] = str.ch[i+j];
		j++;
	}
	substr.ch[j] = '\0';
	substr.length = len;
	return 1;
}

串清空

int clear(Str& str){
	if(str.ch){
		free(str.ch);
		str.ch = NULL;
	}
	str.length = 0;
	return 1;
}

KMP算法

求next数组

F：P1P2…Pj-1Pj

最长公共前缀 FL：P1 P2…Pt-2 Pt-1

最长公共后缀 FR：Pj-t+1 Pj-t+2…Pj-2Pj-1

在这里插入图片描述

状态定义

t：当前F最长相等前后缀的 长度

next[j+1]：记录模式串第j+1个字符不匹配时，模式串中重新与主串比较的字符的下标位置

状态转移方程
n e x t [ j + 1 ] = { t + 1 p t = p j n e x t [ t ] + 1 p t ≠ p j , p n e x t [ t ] = p j n e x t [ n e x t [ t ] ] + 1 p t ≠ p j , p n e x t [ t ] ≠ p j , p n e x t [ n e x t [ t ] ] = p j … … next[j+1]= \begin{cases} t+1 &p_t=p_j \\ next[t]+1 &p_t≠p_j, p_{next[t]}=p_j \\ next[next[t]]+1 &p_t≠p_j,p_{next[t]}≠p_j,p_{next[next[t]]}=p_j& \\ ……\\ \end{cases} next[j+1]=⎩⎪⎪⎪⎨⎪⎪⎪⎧​t+1next[t]+1next[next[t]]+1……​pt​=pj​pt​​=pj​,pnext[t]​=pj​pt​​=pj​,pnext[t]​​=pj​,pnext[next[t]]​=pj​​​

初始化

n e x t [ 1 ] = 0 next[1] = 0 next[1]=0

void getNext(Str substr, int next[]){
	int j = 1, t = 0;
	next[1] = 0;
	while(j<substr.length){
		if(t == 0 || substr.ch[j] == substr.ch[t]){
			next[j+1] = t + 1;
			j++;
			t++;
		}else{
			t = next[t];
 ******************************************************************
 *最长相等前后缀长度 更新为 该长度下不匹配时，重新比较的字符 在模式串中的位置*
 ******************************************************************
   		}
	}
}

练习
在用KMP算法进行模式匹配时、模式串“ababaaababaa”的next数组值为

最长前后缀tababaaababaa
0a0
0b1
0a1
a1b2
ab2a3
aba3 a4
a1 a2
a1 b2
ab2 a3
aba3 b4
abab4 a5
ababa5 a6

Answer: 0，1，1，2，3，4，2，2，3，4，5，6

KMP算法

假定存储序号为1……n, i 指向主串，j 指向模式串
i 不回溯
j 超出范围 ⇨ 匹配成功 ⇨ 返回模式串在主串中的初始位置

int KMP(){
	int i = 1, j = 1;	
	while(i<=str.length && j <= strsub.length){
		if(j == 0 || str.ch[i] == substr.ch[j]){	   
			i++;	
			j++;
		}else{
			j = next[j]；
		}
	}
	if（j>substr.length）{	
		return i - substr.length;
	}else{
		return 0;
	}
}

KMP的改进

原因

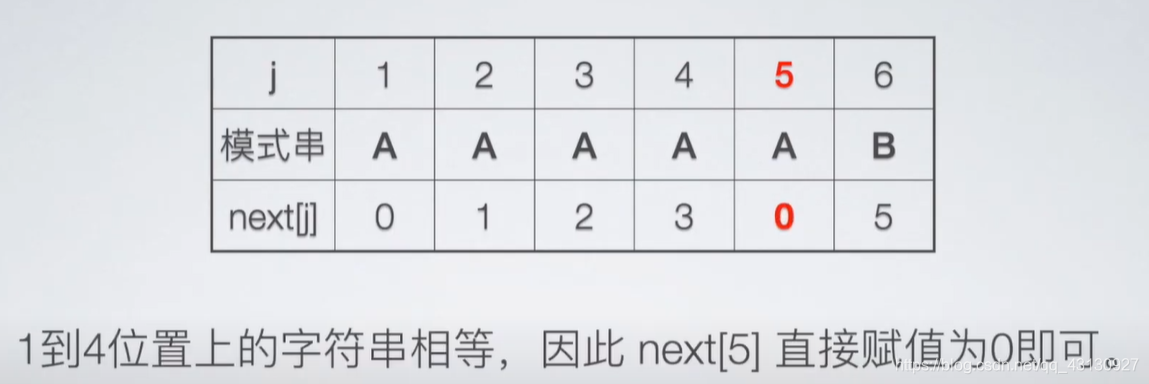
在这里插入图片描述

j = 5 j = 5 j=5 时
n e x t [ 5 ] = n e x t [ 4 ] next [5] = next[4] next[5]=next[4]
n e x t [ 4 ] = n e x t [ 3 ] next [4] = next[3] next[4]=next[3]
n e x t [ 3 ] = n e x t [ 2 ] next [3] = next[2] next[3]=next[2]
n e x t [ 2 ] = n e x t [ 1 ] next [2] = next[1] next[2]=next[1]

问题
 过多的回溯
思考
 能否记忆化上个 n e x t [ j ] next[j] next[j]
在这里插入图片描述

在这里插入图片描述

状态转移方程
n e x t v a l [ j ] = { 0 j = 1 n e x t [ j ] p j ≠ p n e x t [ j ] n e x t v a l [ n e x t [ j ] ] p j = p n e x t [ j ] nextval[j]= \begin{cases} 0 &j=1 \\ next[j] &p_j≠p_{next[j]}\\ nextval[next[j]] &p_j=p_{next[j]} \\ \end{cases} nextval[j]=⎩⎪⎨⎪⎧​0next[j]nextval[next[j]]​j=1pj​​=pnext[j]​pj​=pnext[j]​​

代码

void getnextval(Str substr, int nextval[]){
	int j = 1, t = 0;
	nextval[1] = 0;
	while(j<substr,length){
		if(t == 0 || substr.ch[j] == substr.ch[t]){
			j++;
			t++;
			if(substr.ch[j] != substr.ch[t]){
				nextval[j] = t;
			}else{
				nextval[j] = nextval[t];
			}
		}else{
			t = nextval[t];
		}
	}
}

练习
在用KMP算法进行模式匹配时、模式串“ababaab”的nextval数组值为

首先求出next数组

模式串ababaab
j j j1234567
n e x t [ j ] next[j] next[j]0112342
   </tr>
next[j]next[j]字符当前字符是否相等ababaab
0a0
1ab✗next[2]
1aa✔nextval[next[3]]
2bb✔nextval[next[4]]
3aa✔nextval[next[5]]
4b a✗next[6]
2b b✔nextval[next[5]]

Answer: 0，1，0，1，0，4，1

综合应用题

  1. 将串str中所有值为ch1的字符转换成ch2的字符，如果str为空串，或者串中不含值为ch1的字符则什么都不做

    void swap(Str &str, char ch1, char ch2){
	for(int i = 0; i<str.length; i++){
		if(str.ch[i] == ch1){
			str.ch[i] = ch2;
		}
	}
}

  2. 实现串str的逆转函数，如果str为空串，则什么都不做

    void swap(char &ch1, char &ch2){
	char temp = ch1;
	ch1 = ch2;
	ch2 = temp;
}
void reverse(Str &str){
	int i = 0, j = str.length - 1;
	while(i<j){
		swap(str.ch[i], str.ch[j]);
		i++;j--;
	}
}

  3. 删除str中值为ch的所有字符，如果str为空串，或者串中不含值为ch的字符，则什么都不做

    void delete(Str &str, char ch){
	if(str.length == 0)
		return;
	int sum = 0, i, j;
	for(i = 0; i<str.length; i++){
		if(str.ch[i] == ch){
			sum++;
		}
	}
	if(sum != 0){
		char *temp_ch = (char*)malloc(sizeof(char)*(str.length - sum+1)){
			for(i = 0, j = 0; i<str.length; i++){
				if(str.ch[i] != ch){
					temp_ch[j++] = str.ch[i]; 
				}
			}
			temp_ch[j] = '\0';
			str.length = str.length - sum;
			free(str.ch);
			str.ch = temp_ch;
		}
	}
}

  4. 从串str中的pos位置起，求出与 substr串匹配的子串的位置，如果str为空串，或者串中不含与sbsr匹配的子串，则返回－1做标记

    int KMP(Str str, Str substr, int pos){
	int i = pos, j = 1;
	while(i<=str.length && j <= substr.length){
		if(j == 0 || str.ch[i] == str.ch[j]){
			++i;
			++j;
		}else{
			j = next[j];
		}
	}
	if(j > substr.length)
		return i - substr.length;
	else
		return -1;
}

  5. 采用定长顺序存储表示串，编写一个函数，删除串中从下标为 i i i的字符开始的 j j j个字符，如果下标为 i i i的字符后没有足够的 j j j个字符，则有几个删除几个

    void delete(Str& str, int i, int j){
	if(i<str.length && i>=0 && j>=0){
		for(int k = i + j; k<str.length; k++){
			str.ch[k - j] = str.ch[k];
		}
		**************************************************
		str.length -= (str.length-i<j? str.length - i: j);
		**************************************************
		str.ch[str.length] = '\0';
	}
}

  6. 采用顺序存储方式存储串，编写一个函数，将串 s t r 1 str1 str1中的下标 i i i到下标 j j j之间的字符（包括i和两个位置上的字符）用 s t r 2 str2 str2串替换

    int concat(Str& str, Str str1, Str str2){
	if(str.ch){
		free(str.ch);
		str.ch = NULL;
	}
	str.ch = (char*)malloc(sizeof(char) * (str1.length + str2.length + 1))
	if(str.ch == NULL){
		return false;
	}
	int i = 0;
	while(i<str1.length){
		str.ch[i] = str1.ch[i];
		i++;
	}
	int j = 0;
	while(j<str2.length){
		str.ch[i+j] = str2.ch[j];
		j++;
	}
	str.length = str1.length + str2.length;
	return true;
}

int subString(Str &substr, Str str, int pos, int len){
	if(pos<0 || pos>=str.length || len<0 || len>str.length-pos)
		return false;
	if(substr.ch){
		free(substr.ch)
		substr.ch = NULL;
	}
	if(len == 0){
		substr.ch == NULL;
		substr.length = 0;
		return true;
	}else{
		substr.ch = (char*)malloc(sizeof(char) * (len + 1));
		for(int i = 0; i<len; i++){
			substr.ch[i] = str.ch[pos+i];
		}
		substr.ch[len+pos] = '\0';
		return true;
	}
}

int stuff(Str& str1, Str str2, int i, int j){
	Str strl1; strl1.ch = NULL; strl1.length = 0;
	Str strl2; strl2.ch = NULL; strl2.length = 0;
	Str temp_str;
	if(!subString(strl1, str1), 0, i)
		return 0;
	if(!subString(strl2, str1, j+1, str1.length-j-1))
		return 0;
	if(!concat(temp_str, strl1, str2))
		return 0;
	if(!concat(str1, temp_str, strl2))
		return 0;
	return 1;
}

  7. 编写一个函数，计算一个子串在一个主串中出现的次数，如果该子串不出现，则返回0。本题不需要考虑子串重叠，如：主串为aaaa，子串为aaa，考虑子串重叠结果为2，不考虑子串重叠结果为1

    int count(Str str, Str substr){
	int i = 1, j = 1, k = 1, sum = 0;
	while(i<=str.length){
		if(str.ch[i] == substr.ch[j]){
			i++;j++;
		}else{
			j = 1;
			i = ++k;
		}
		if(j>substr.length){
			j = 1;
			sum++;
		}
	}
	return sum;
}

  8. 构造的链表结点数据结构（每个结点内存储一个字符），编写一个函数，找出串 s t r 1 str1 str1中第一个不在 s t r 2 str2 str2中出现的字符

    typedef struct SNode{
	char data;
	Struct SNode *next;
}

char findfirst(SNode *str1, SNode *str2){
	for(SNode *p = str1; p!=NULL; p = p->next){
		bool flag = false;
		for(SNode *q = str2; q!=NULL; q = q->next){
			if(p->data == q->data){
				flag = true;
				break;
			}
		}
		if(flag == false){
			return p->data;
		}
	}
	return '\0';
}

总结

  • 😄
  • 😢
2022天勤数据结构
m0_67118403的博客
02-27 746
第二章 线性表 02 存储结构 设A=（a1，a2，…，am）和B=（b1，b2，…，bn）均为顺序表，A’和B’分别是除去最大公共前缀后的子表。例如，A=（b，e，i，j，i，n，g），B=（b，e，i，f，a，n，g），则两者的最大公共前缀为b、e、i，在两个顺序表中除去最大公共前缀后的子表分别为A’=（j，i，n，g），B’=（f，a，n，g）若A’=B’=空表，则A=B。若A’=空表且B’≠空表，或两者均不为空且A’的第一个元素值小于B’的第一个元素值，则A<B，否则A>B。所有表中
天勤2022数据结构（一）线性表
Zheng_LH
03-16 2462
天勤2022数据结构（一）线性表前言一、基础题二、使用步骤1.引入库2.读入数据总结 前言 提示：全文为作者手打，仅供个人复习使用 一、基础题 线性表可用顺序表和链表存储，试问： 如果有n个表同时并存，并且在处理过程中各表的长度会动态发生变化，表的总数也可能自动改变，在此情况下，应选用哪种存储表示？为什么？ 用链表。如果采用顺序表，在多个表并存的情况下，一旦发现某个表有存满并溢出的情况，很可能 若表的总数基本稳定，且很少进行插入和删除但要求以最快的速度存取表中的元素，这时用哪种存储表示？为
天勤数据结构
08-15
解压后,包含两个PDF文件,天勤数据结构近两年的版本(2018版/2019版),资源不用介绍,你们都有备而来,一起学习吧
天勤2022数据结构（二）栈和队列
Zheng_LH
03-24 634
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录前言一、顺序栈操作二、链栈2.读入数据总结 前言 顺序栈 typedef struct{ int top; int data[maxSize]; }SqStack; 链栈结点 typedef struct LNode{ int data; struct LNode *next; }LNode; 顺序队列 typedef struct{ int front; int rear; int data[maxSize]
天勤2022数据结构（五）树与二叉树
Zheng_LH
04-21 387
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录前言一、综合应用题总结 前言 提示：这里可以添加本文要记录的大概内容： typedef struct{ }BTNode; 提示：以下是本篇文章正文内容，下面案例可供参考 一、综合应用题 设二叉树根结点所在层次为1，树的深度d为距离根最远的叶结点所在的层次 试精确给出深度为d的完全二叉树的不同二叉树棵数 2(d−1)2^{(d-1)}2(d−1) 试精确给出深度为d的满二叉树的不同二叉树棵数 1
2020 天勤数据结构 高分笔记 + 习题
03-31
这份“2020 天勤数据结构 高分笔记 + 习题”资源包含了两个关键部分，即高分笔记和习题集，旨在帮助考生深入理解和应用数据结构的基本概念、算法和设计方法。 首先，让我们详细探讨一下数据结构的基础知识： 1. **...
天勤2019数据结构
11-17
《天勤2019数据结构》是一本针对初学者和考研学生的专业教材，主要涵盖了数据结构这一核心的计算机科学主题。数据结构是计算机科学的基础，它研究如何在内存中组织和管理数据，以实现高效的算法。对于计算机专业的...
天勤2019数据结构全套视频 天勤考研资料视频下载
09-25
天勤2019数据结构全套视频，包含基础知识、串、图、排序、数组、矩阵、广义表、查找、栈和队列、树、算法、线性表等
数据结构-天勤
qq_41497658的博客
08-17 637
这里写自定义目录标题欢迎使用Markdown编辑器新的改变功能快捷键合理的创建标题，有助于目录的生成如何改变文本的样式插入链接与图片如何插入一段漂亮的代码片生成一个适合你的列表创建一个表格设定内容居中、居左、居右SmartyPants创建一个自定义列表如何创建一个注脚注释也是必不可少的KaTeX数学公式新的甘特图功能，丰富你的文章UML 图表FLowchart流程图导出与导入导出导入 欢迎使用Markdown编辑器 你好！ 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Mar
天勤数据结构：前缀、中缀、后缀表达式的转换与计算
热门推荐
寒泉
08-20 6万+
第三章 栈和队列 1. 输出队列问题 2. 表达式的转换 - 手工转换 2.1 中缀表达式 转 前缀表达式 2.2 中缀表达式 转 后缀表达式 2.3 后缀表达式 转 中缀表达式 2.4 后缀表达式 转 前缀表达式 3. 表达式的转换 - 用栈实现 3.1 中缀转后缀 代码 3.1 中缀转前缀 3.2 后缀转前缀 4. 表达式求值 - 用栈实现 4.1 中缀表达式求值 4.2 后缀表达式求值 4.3 前缀表达式求值 ...
《天勤2019年数据结构》
10-14
《天勤2019年数据结构》
天勤2019 数据结构
09-28
数据结构 考研
2019天勤数据结构
09-05
简单易懂的数据结构PDF，适合零基础理解晦涩难懂的数据 结构
天勤数据结构视频资料学习.zip
09-14
考研天勤视频课，天勤相对王道来说易懂一些，比较通俗易懂
天勤数据结构——绪论
xun08042的博客
07-19 838
数据类型 结构型 结构体 指针型 int *a；//指向字符型变量的指针a，这里只是定义一个变量名，还没指向地址 如果a是个指针型变量，且它已经指向了一个变量b，则a中存放变量 b所在的地址。*a就是取变量b的内容（x=*a;等价于x=b;)，&b就是取变量b的地址，语句 a=&b;就是将变量b的地址存于a中，即大家常说的指针a指向b。 结点的构造 链表结点 typedef struct Node { int data ; //这里默认的是int型，如需其他类型可修改 struc
天勤 数据结构 P80 T10
Cainell的博客
08-14 208
题目 试编写一个算法，检查一个程序中的花括号、方括号和圆括号是否配对，若全部配对，则返回1，否则返回0。对于程序中出现的一对单引号或者双引号内的字符不进行括号配对检查。39为单引号ASCII值，34为双引号的ASCII值。单引号和双引号如果出现则成对出现。 int bracketsCheck(char f[]){// 对由字符数组f所存字符中的文本进行括号匹配检查 stack S, char ch; char *p = f; while(*p!='\0'){// 顺序扫描串中的每一个字符
天勤2022数据结构（四）数组、矩阵与广义表
Zheng_LH
04-13 658
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录前言一、综合应用题总结 前言 提示：这里可以添加本文要记录的大概内容： 提示：以下是本篇文章正文内容，下面案例可供参考 一、综合应用题 设数组A［0，…，n－1］的n个元素中有多个零元素，设计一个算法，将A中所有的非零元素依次移动到A数组的前端 void move(int A[], int n){ int i = -1, j, temp; for(j = 0; j<n; j++){ if(A[j] != 0)
数据结构--基于天勤--数组表
一个非计算机专业的 博客
12-23 295
/* 顺序表（数组实现） 2018.12.04 编写 */ #include&lt;stdio.h&gt; #define MAXSIZE 1000 typedef struct {     int data[MAXSIZE];//数组元素     int length;//数组长度 }SequenceList; //初始化、并进行元素赋值 void init(SequenceList...
天勤2019年数据结构详解与应用
《天勤2019数据结构》是一本专注于数据结构这一核心计算机科学主题的教材或参考书。数据结构是计算机科学与技术专业中的一个重要基础课程，它主要研究如何高效地存储、组织和处理数据，以及如何选择合适的数据结构以...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值