图像分析中的形态灰度重建：应用和高效算法 论文翻译1

论文作者：Luc Vincent

论文符号定义：
图像I是离散平面Z2的有限矩形子集DI到离散灰度集的映射{0，1，…，N-1}。二进制图像I只能是0或者1这两个值中一个。在本文中，经常使用Z2来代替二进制离散集合。类似的，灰度图被看成函数或者映射。

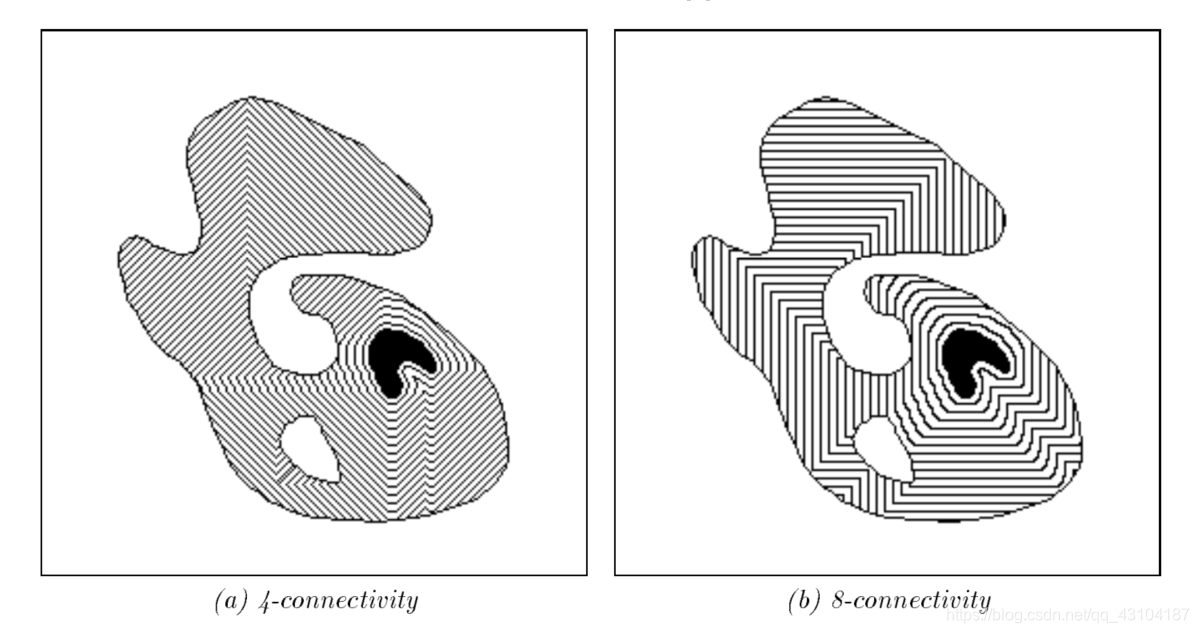
离散网格G包含于Z2Z2*提供了像素之间的邻域关系。当且仅当（p,q）属于G时，p和q是邻域关系。这篇文章我们将使用4邻域或者8邻域或者如图2所示的六角形网格。不过请注意，下面描述的算法适用于任何维度，任何尺寸的网格。

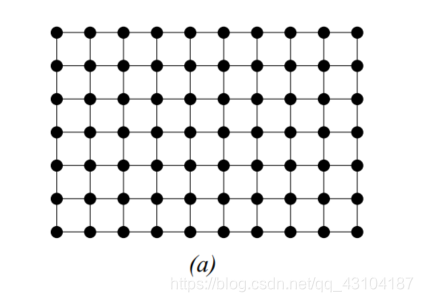
4邻域

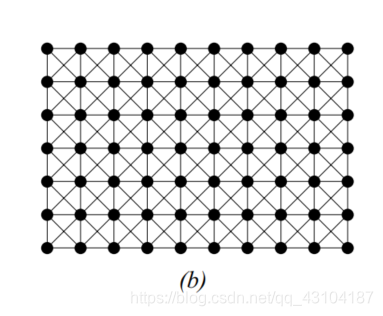
8邻域

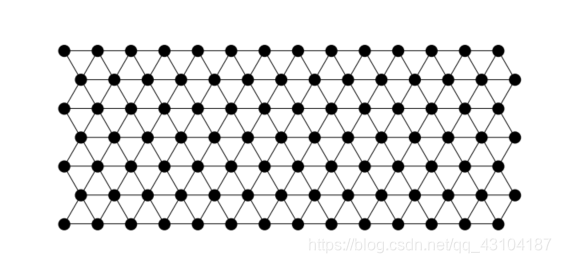
六角形

在Z2上的G的距离dG:dG(p,q)表示为像素p到像素q穿过的网格边的最小数量。在4邻域中这被称作城区距离，在8邻域中这被称为棋盘距离。我们用NG§表示在网格G上p的邻域集合。

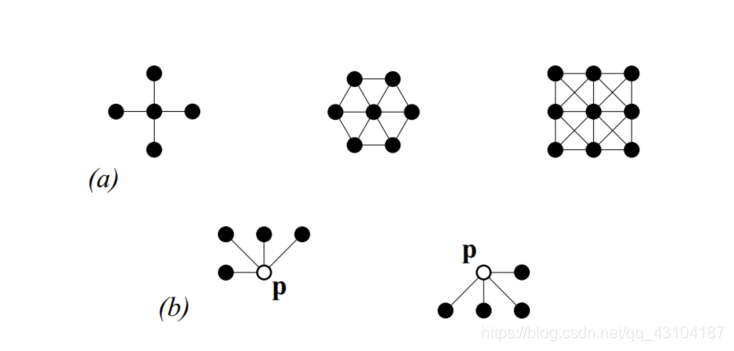
1 Reconstruction for binary images

1.1 Defination in terms of connected components

I 和 J 是同一个离散定义域 D 上的两个二值图像，使得J包含于I。
从映射的角度看，这意味着对于任意的J§ = 1 有I§ = 1。J为标记图像，I为遮罩。定义I1，I2,…In为I的连通域。

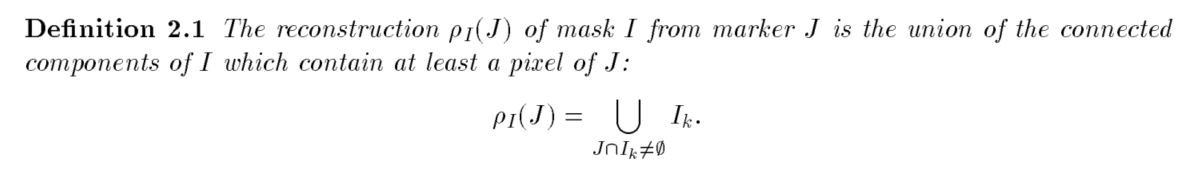
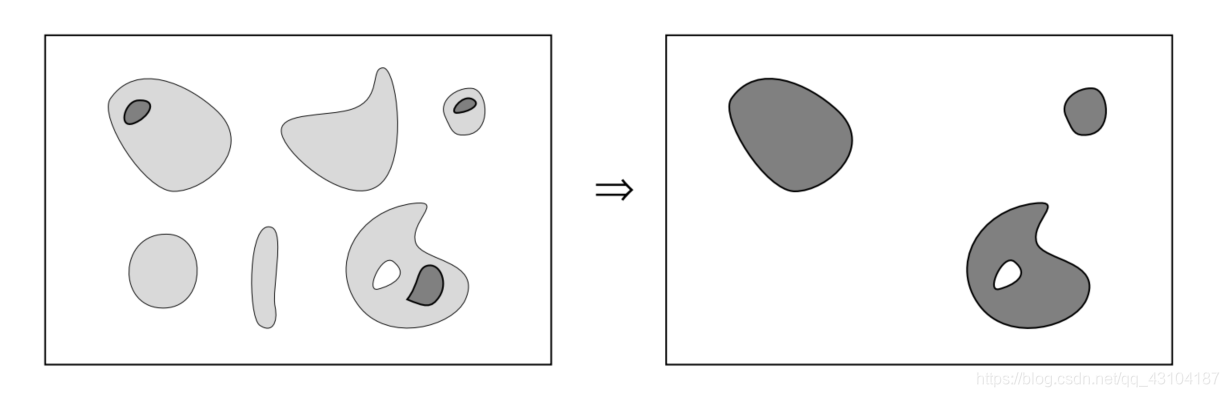
我的理解是J是左图中深色部分，I是左图中浅色部分。两图交集为深色部分，在I中与两者交集有关联的有三个连通域，从标记到连通域的重构就是由两者的交集为种子，生长满其所在的连通域，
这个概念非常简单，但却产生了一些很有趣的应用程序和扩展。

1.2 Definition in terms of geodesic distance

大部分时间描述重构的定义都是通过距离的概念。给定（mask）集合X，像素p和像素q之间的距离是集合X中包含的连接p与q的最短路径的长度。值得注意的是（Mask）X中的距离取决于所使用的连接类型。

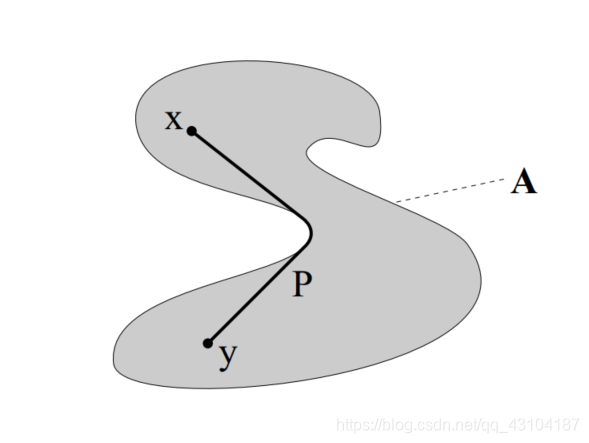
1981年，Lantu ejoul和Beucher 在图像分析框架中引入了距离，它是几种形态学算子的基础。可以利用以下定义膨胀（腐蚀类似）：

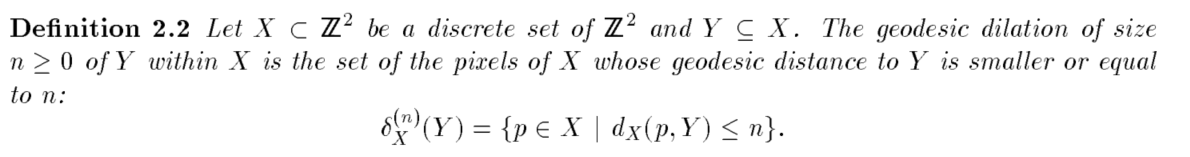
腐蚀和膨胀（距离定义）
曲面上两点间距离最短的线：geodesic

模拟种子点生长，膨胀再与MASK的交集。

在Mask X内对集合Y执行连续的膨胀，与Y交集不为空的X的连通域将逐渐被填满。从而给出如下定义：

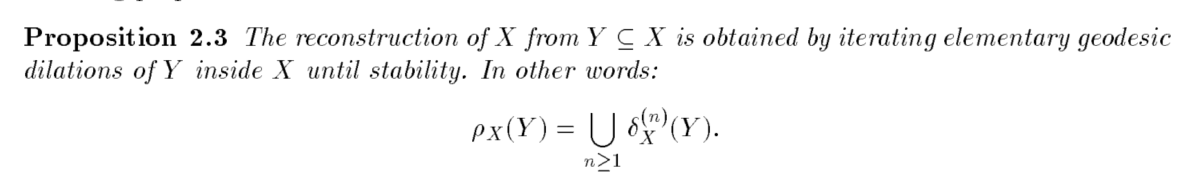
1.3 Grayscale reconstruction

1.3.1 Definition using threshold superposition

近几年来可知，至少在离散领域，在二值图像上的任何新增的变换都可以扩展到灰度图像上。所谓的扩展指的是：

（这一段我翻译太差）大体可以理解为越高的阈值的二值化区域是低阈值的子集。

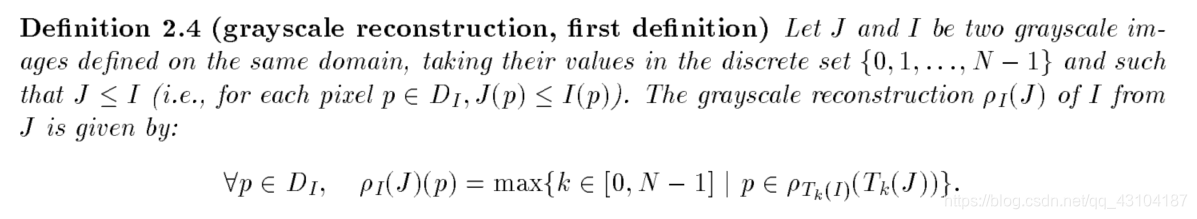
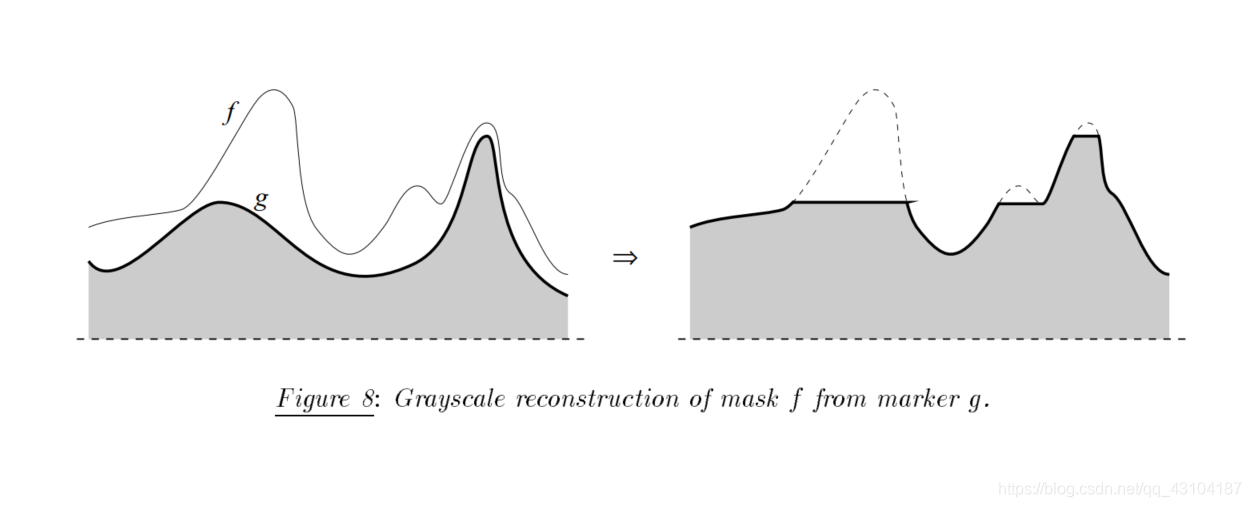
灰度重构更贴近真实世界的图像处理，如何做出h-dome变换依赖于灰度重构。（h-dome方法是我看这篇文章的目的），这里需要加深理解。

简单总结一下：
论文中首先定义了4-邻域，8邻域和六角形邻域，dG是p与q的最短距离，The elementary ball in distance dG is denoted BG , or simply B，NG§是p的邻域。
其次定义了连通域，Let I1, I2, … , In be the connected components of I.I数字代表其连通域中的各个元素。

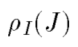
这是标记图像J到掩膜图像I的重构。
第三段定义了最短距离的概念，并用距离的概念描述了基于腐蚀膨胀的重构操作。

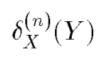
距离运算。

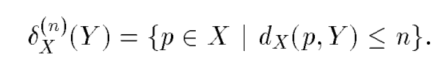
Y为标记图像，Y包含于X，p是X中的点，求取p到Y的距离小于n的集合。

二值图像重构定义：

基于上面的距离概念给出了Y对X的重构

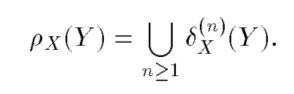
注意：

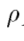
重构运算

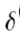
距离运算

在回顾了每个运算符代表的含义之后，再重新理解灰度重构的定义：

首先为了将图像重构概念从二值扩展到灰度图像，引入了


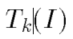
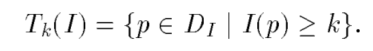
它表示的是图像I中灰度值大于k的点的集合。

T0(I)代表所有灰度值大于0的点的集合，以此类推。

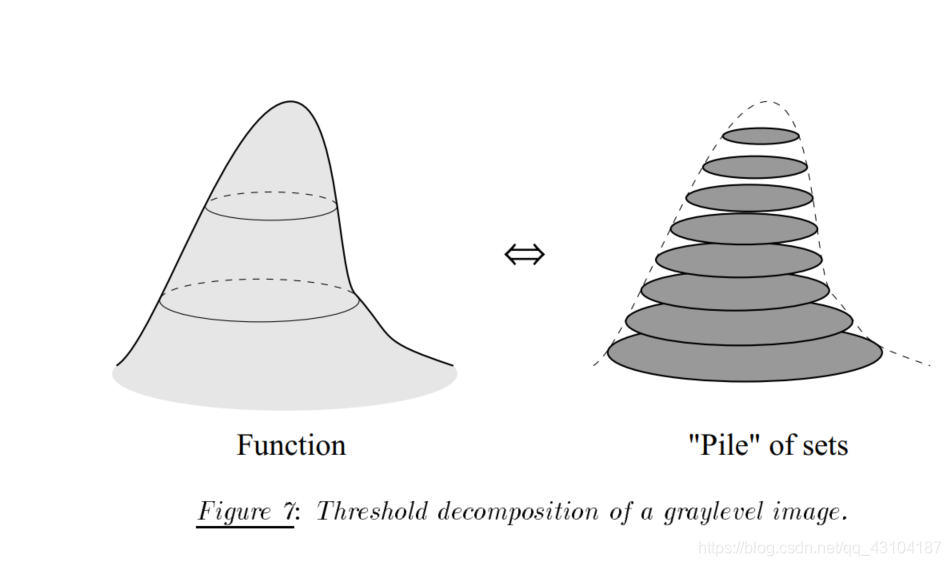
这些阈值将I分层，如下图所示：

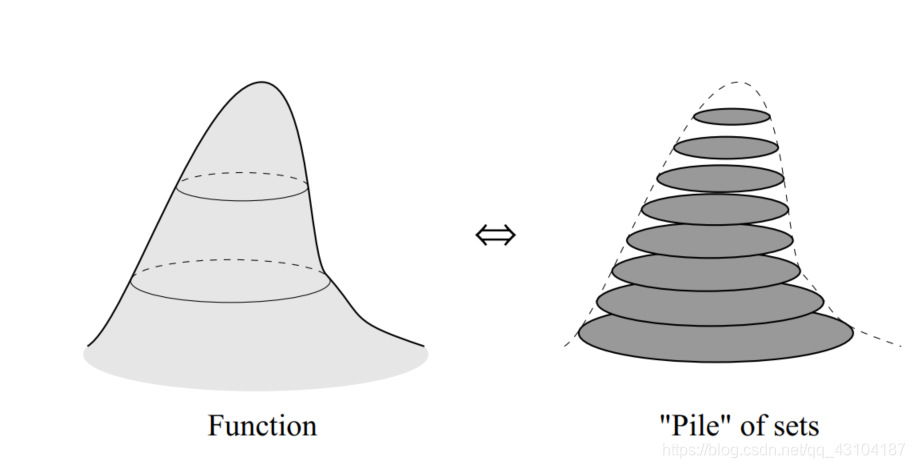
这些集合之间满足如下的包含关系：

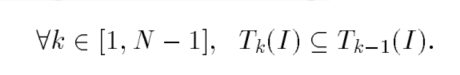
对于这个集合组中的每一个集合的运算仍满足上述包含关系：

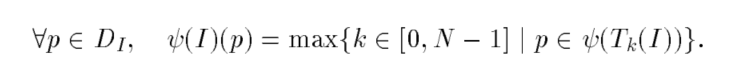
那么对于二值图像来说，这个关系可以反应为：

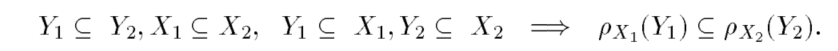
Definition （grayscale reconstruction）

J 和 I 是相同定义域上的两张灰度图像，以离散集合 {0，1，…，N-1} 获取两张图像的灰度值，并且J <= I。从 J 到 I 的灰度重建为：

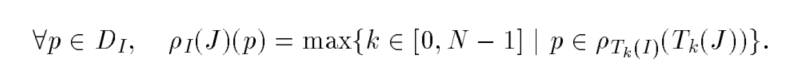
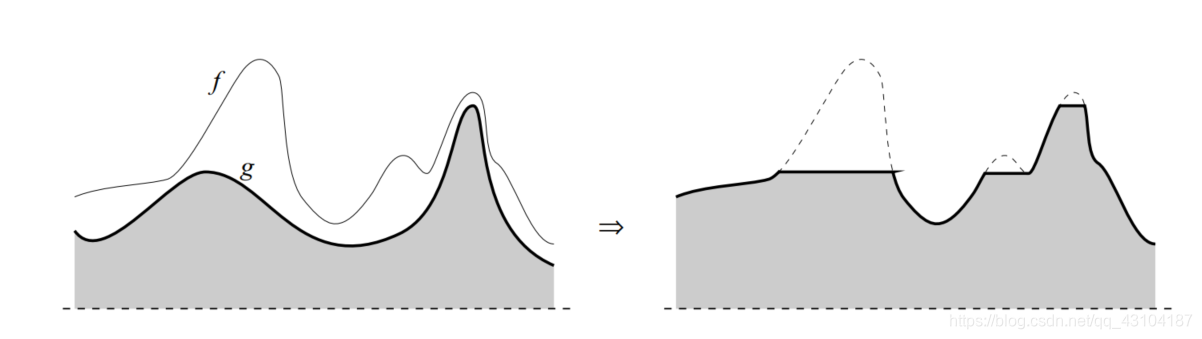
下图说明了这种转换。 就像二进制重建提取标记的marker的那些相连的元素一样，灰度重建提取标记图像标记的marker的峰值。

还是不太明白，虽然单独拿出来的二值化重构很好理解，但灰度我无法去想像会怎样发展，那个max啥意思？？？最大的k？？？。按照概念一步一步模拟着推一下。

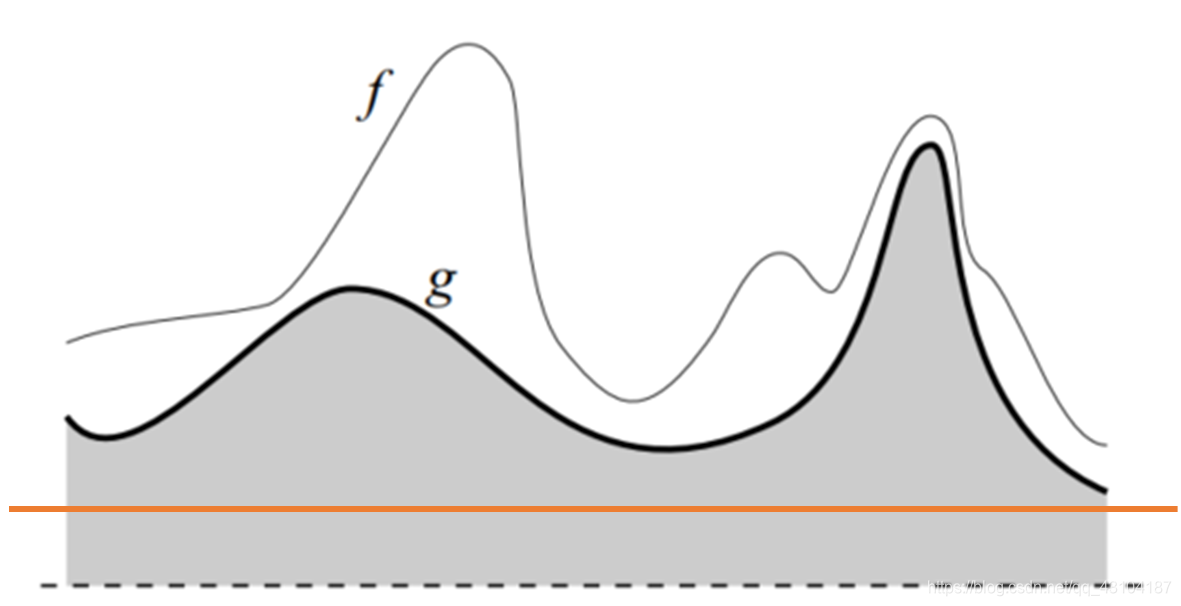
当阈值选择完毕之后，上方值为1，下方值为0，上图选择为全1图，无需重构。

阈值向上增长：

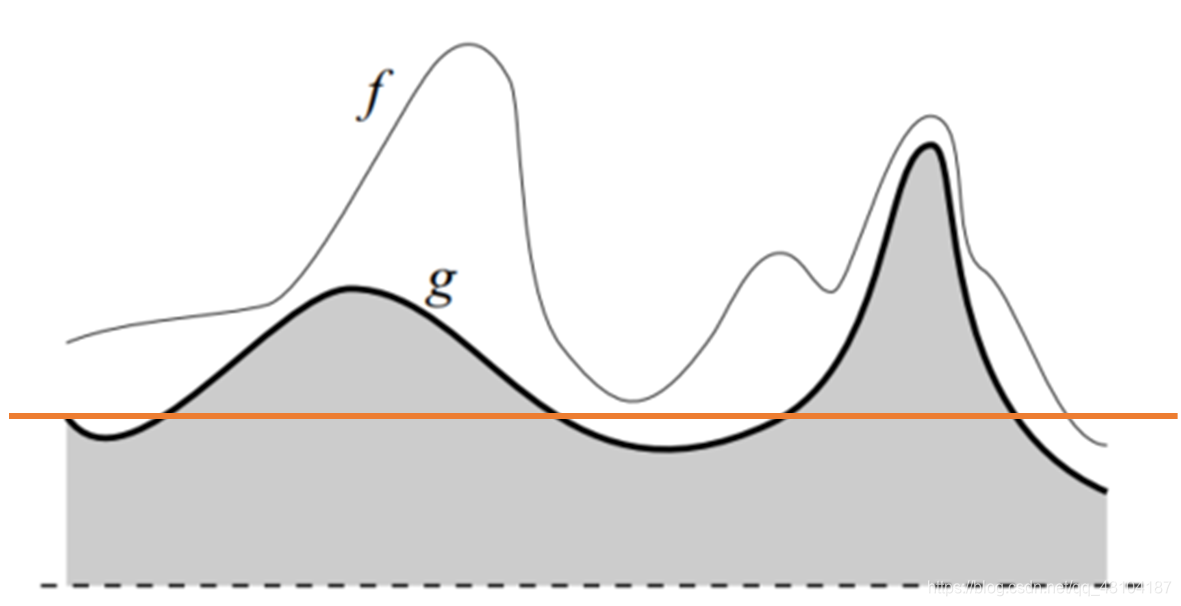
f 图除了最右边一点值为0外全为1，g图为1的值与f重叠，g对f的重构无改变。

阈值继续向上：

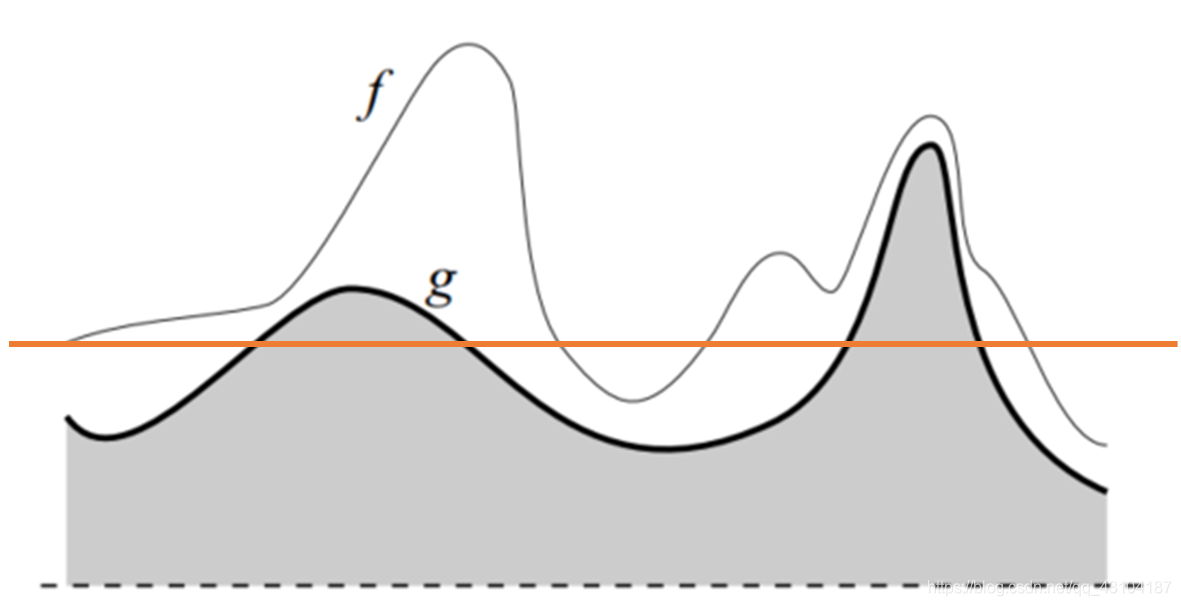
阈值将分为4部分，分别是1，0，1，0。此时g对f的重构为：

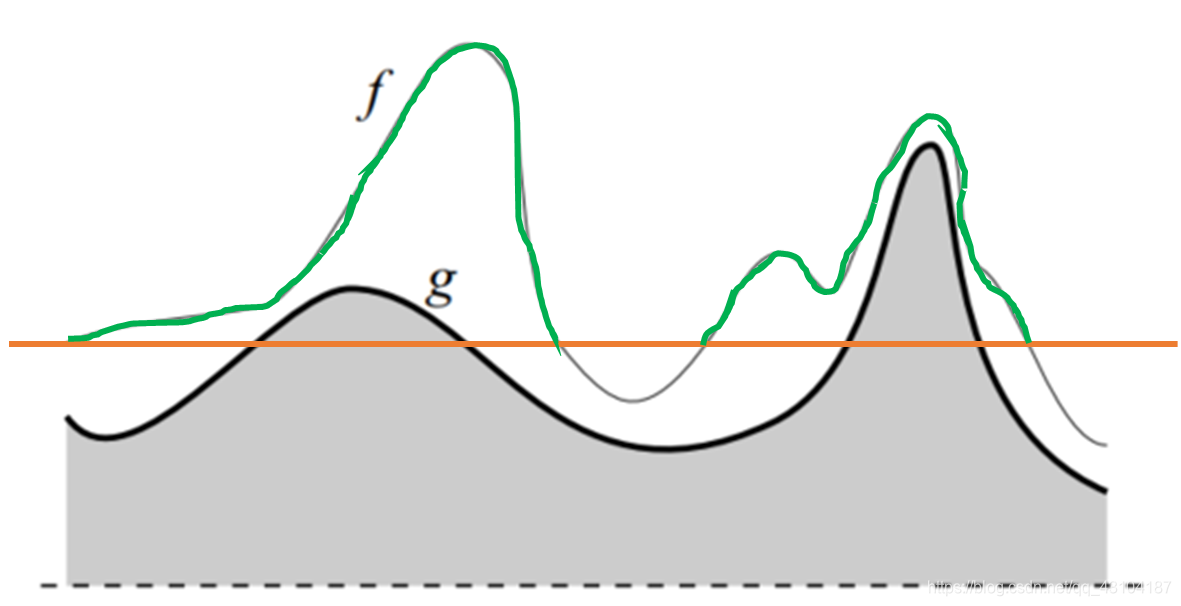
绿色部分为1，其余为0。

阈值再往上：

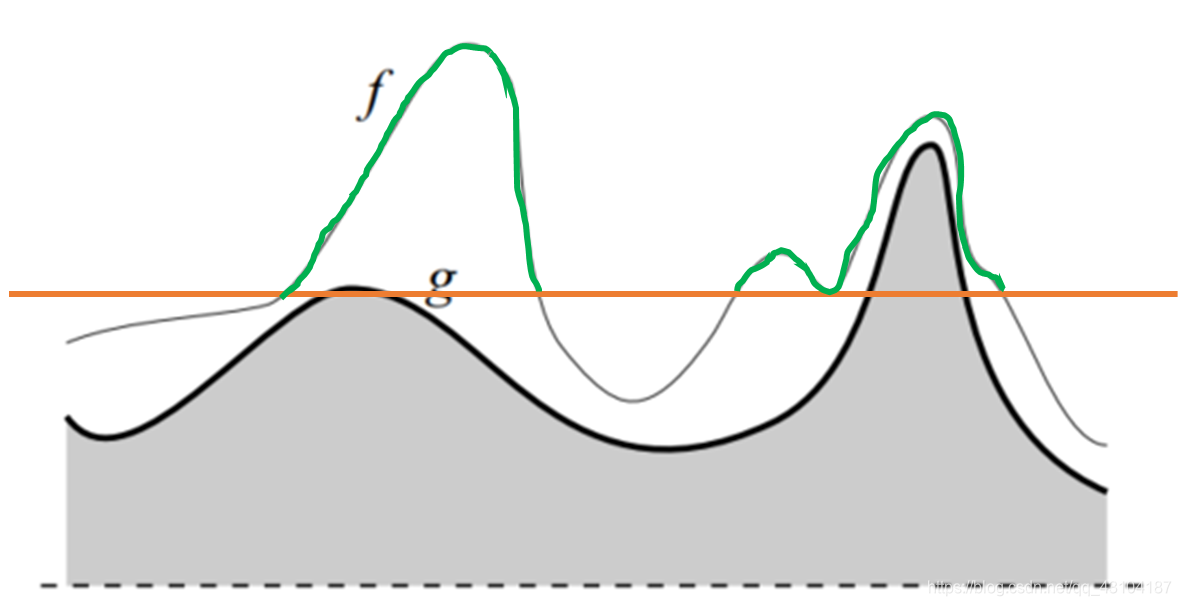
阈值再往上：

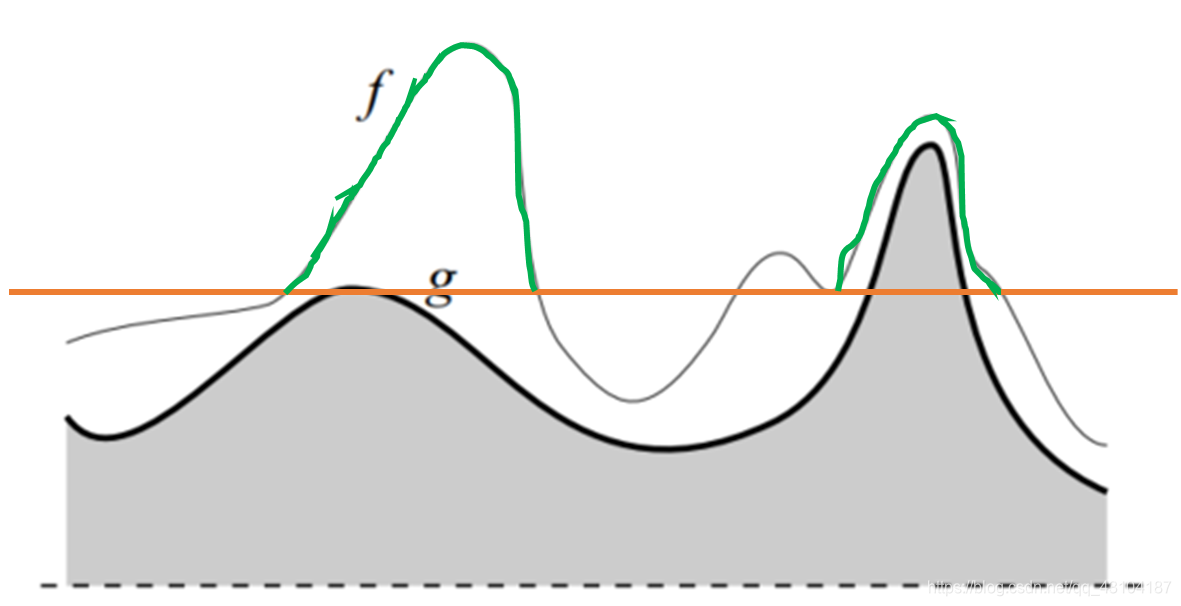
阈值再往上：

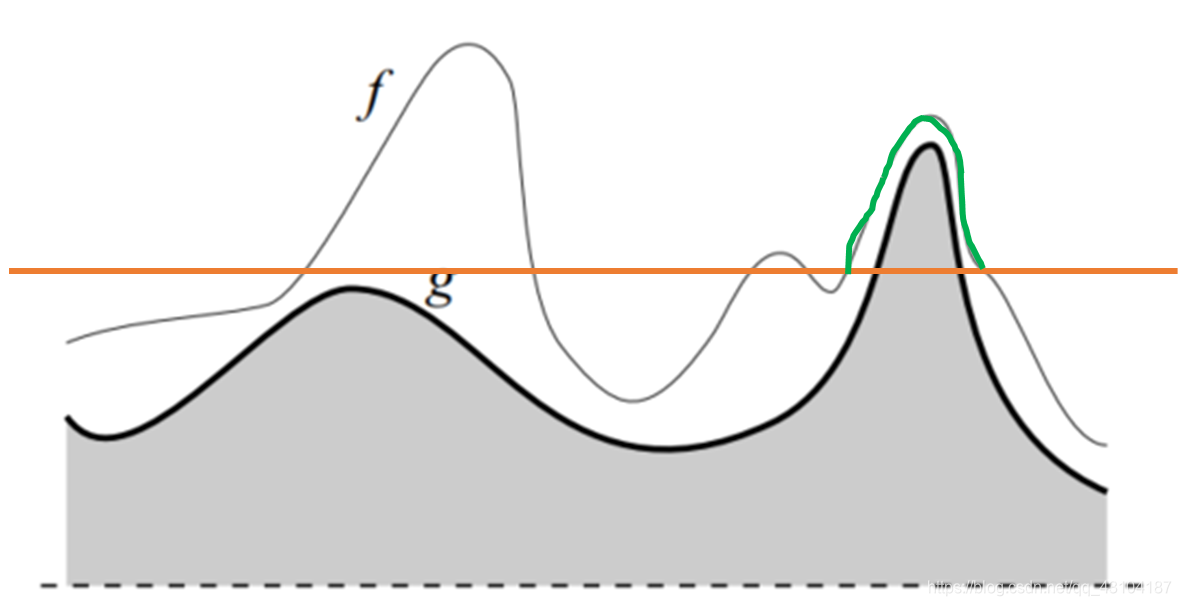
阈值再往上：

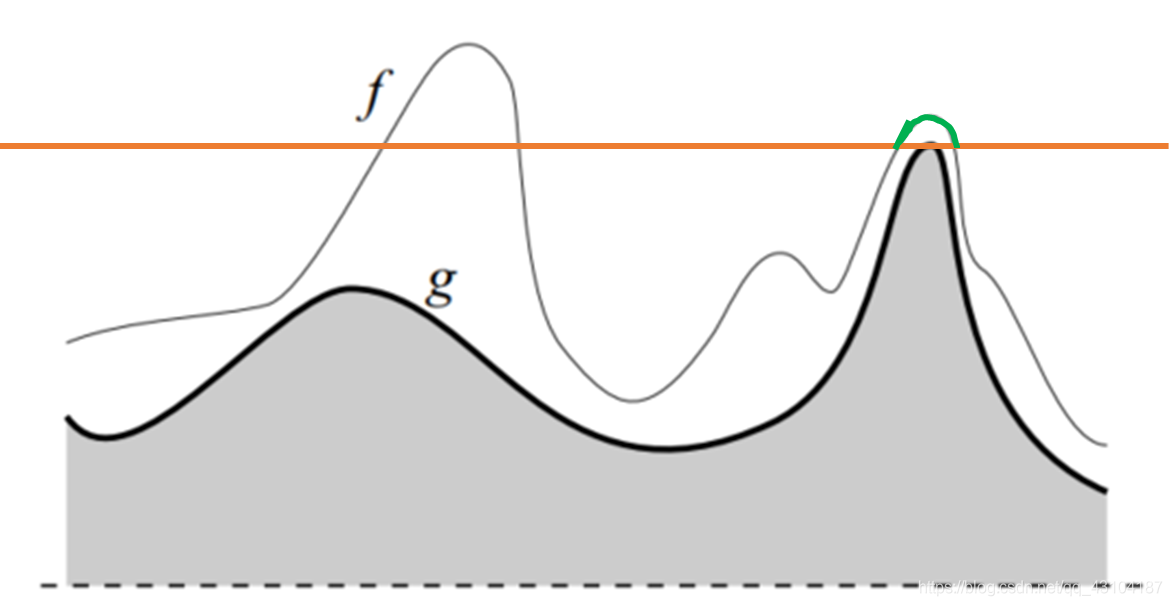
阈值再往上：

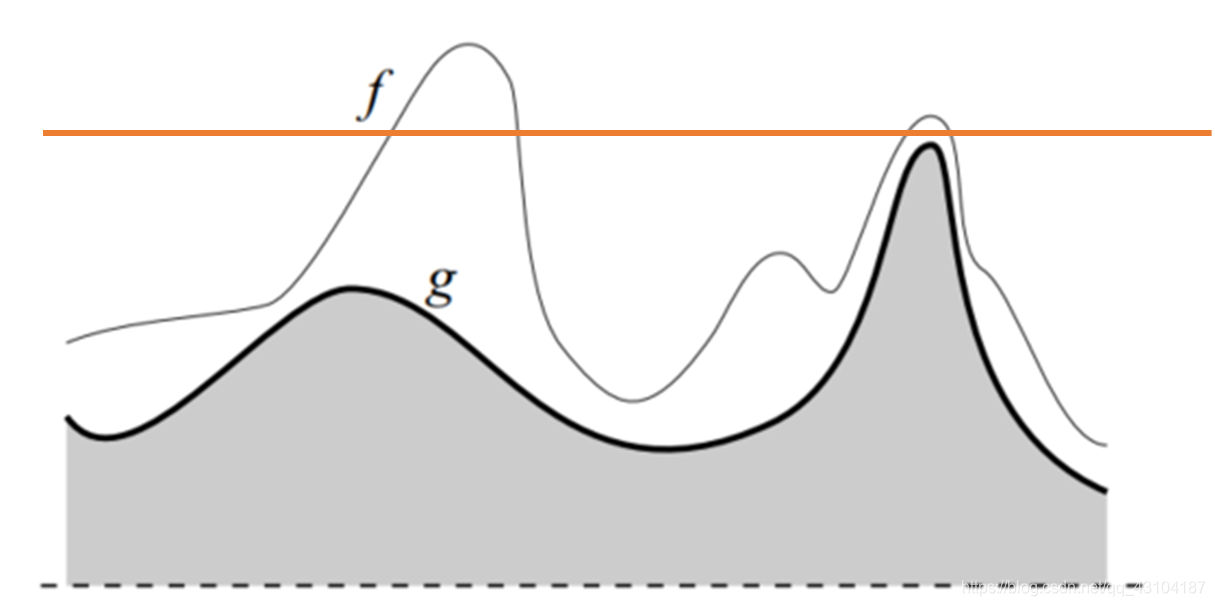
没有种子点，无法膨胀，交集为0。

这个max还是没理解，最大的p值？？？

我是在二值图像中去理解它们的，如果带上本身的阈值呢？

从第一张图像开始分析，

第一张，f 全为1，g全1，本身阈值为f1。那么这一层的重构可以覆盖到全部，重构图的所有点全部赋予f1这个值。

当阈值上升，到 f 的最小的极小值时，这是临界点，再往上种子点的重构无法覆盖到全图像，此时阈值为f2，那么此时最小值点为f2。在第一最小极值点和第二最小极值点之间，根据阈值保留有外轮廓。重构图应该为：

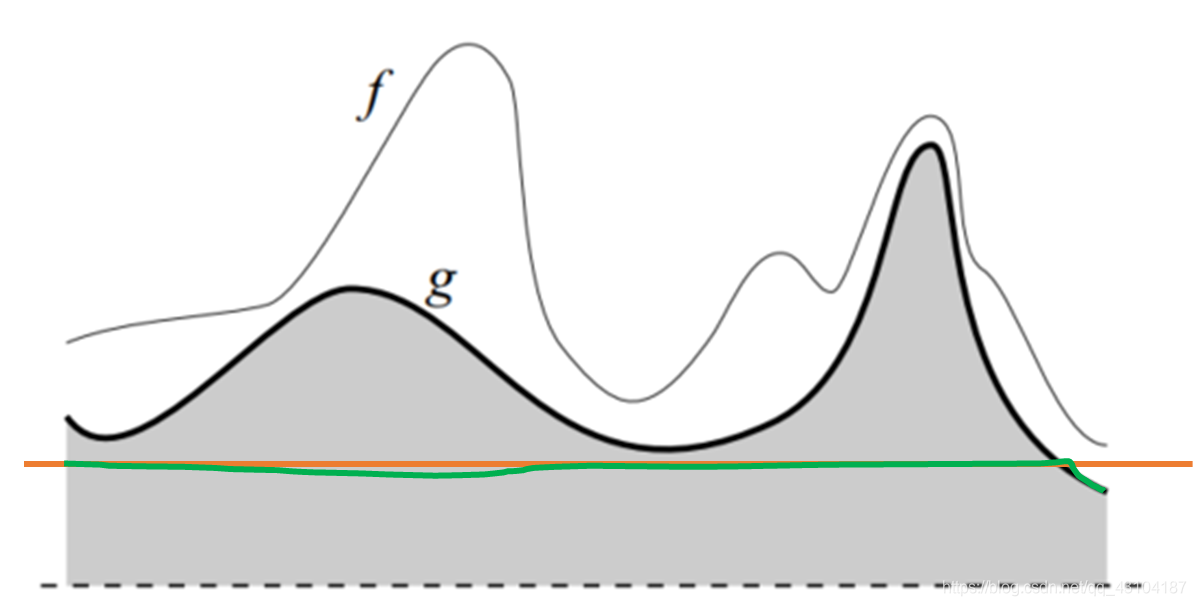
画的有点难看。

阈值继续往上走：

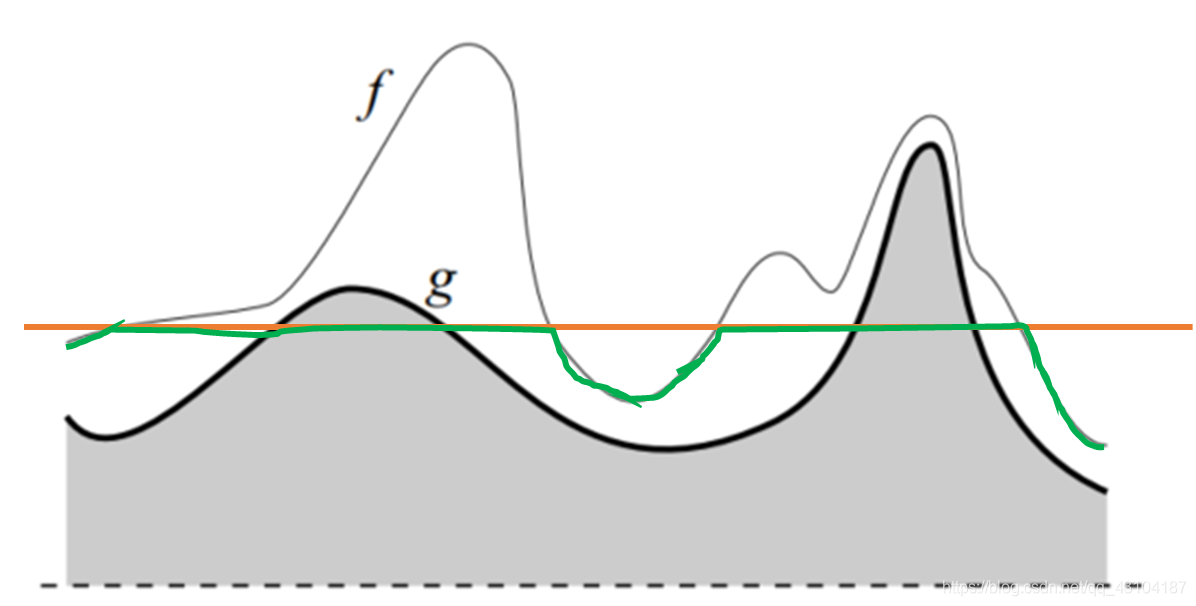
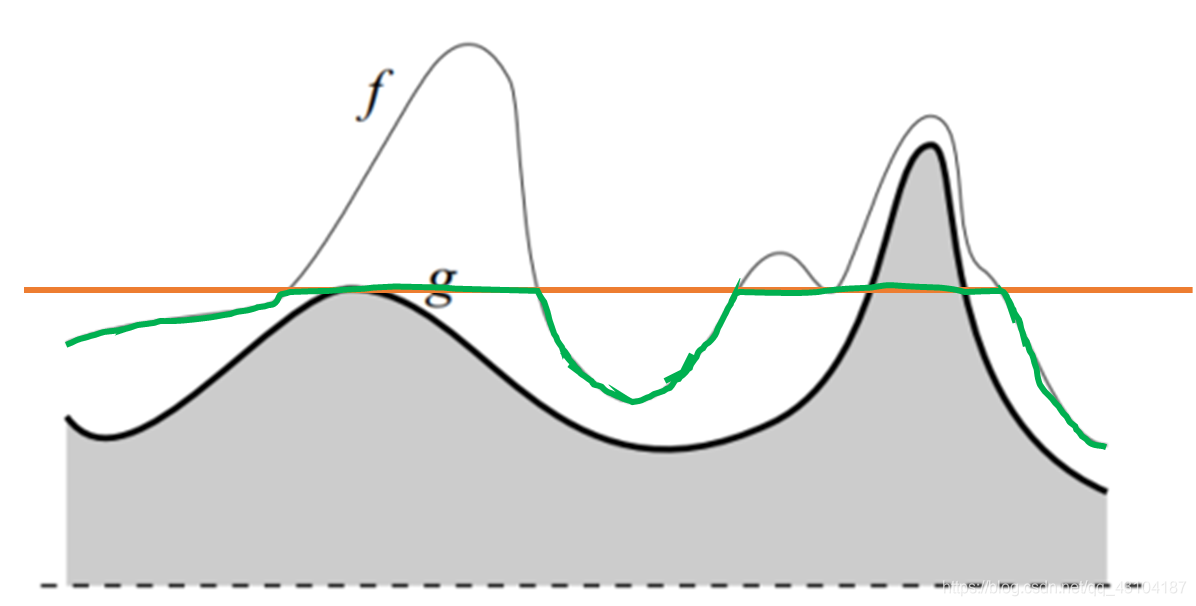
当阈值全部遍历完之后即可得到论文的结果图。

重点
重点
重点

关键点是每一次重构时，两幅图像重构的结果图为1的点赋予这个阈值，其他点保持不变，如此便可计算出最后的结果了。。。

到此概念阶段结束。
论文中的应用实例在下篇博文。