二叉树1：实现二叉树的先序、中序、后序遍历，包括递归方式和非递归方式

二叉树的先序遍历：
1：访问根节点
2：访问左子树
3：访问右子树

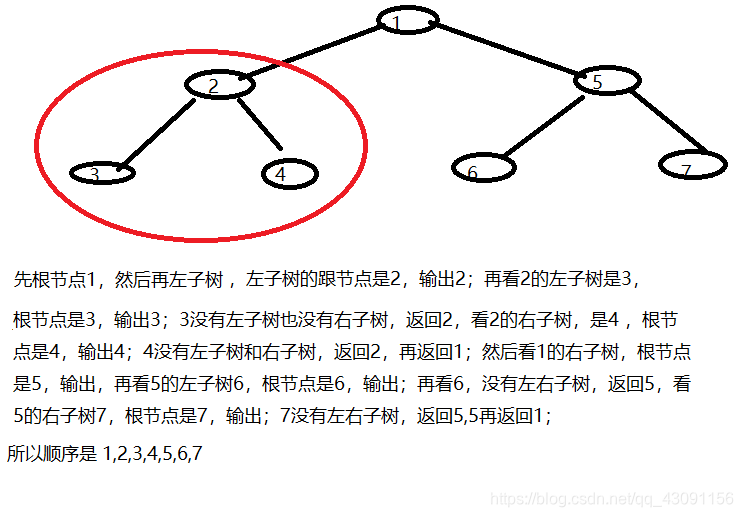
二叉树的中序遍历：
1：中序遍历左子树
2：访问根节点
3：中序遍历右子树

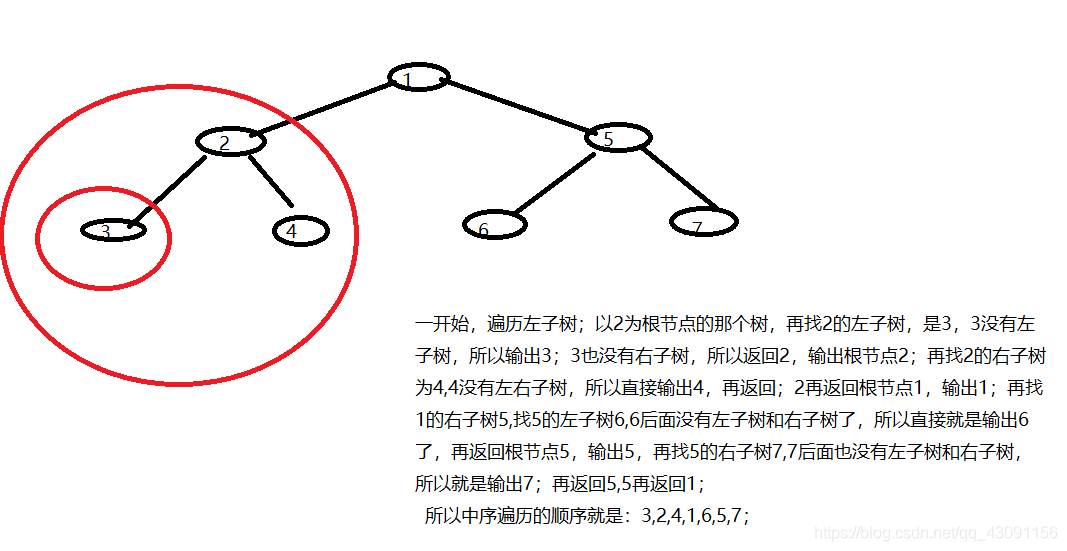
二叉树的后序遍历：
1：后序遍历左子树
2：后序遍历右子树
3：访问根节点

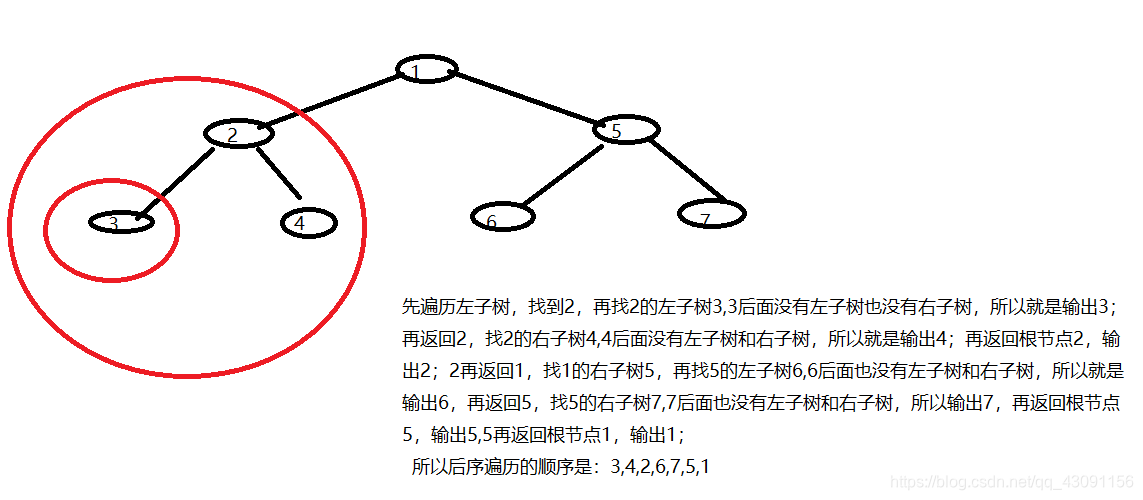
使用递归的方式来实现二叉树的几种遍历：

public class Code_01_PreInPosTraversal {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static void preOrderRecur(Node head) { //递归的方式 先序遍历
		if (head == null) {
			return;
		}
		System.out.print(head.value + " ");
		preOrderRecur(head.left);
		preOrderRecur(head.right);
	}

	public static void inOrderRecur(Node head) { // 递归的方式 中序遍历
		if (head == null) {
			return;
		}
		inOrderRecur(head.left);
		System.out.print(head.value + " ");
		inOrderRecur(head.right);
	}

	public static void posOrderRecur(Node head) { //递归的方式 后序遍历
		if (head == null) {
			return;
		}
		posOrderRecur(head.left);
		posOrderRecur(head.right);
		System.out.print(head.value + " ");
	}

这里的return返回是此函数的结束处，相应的变量的参数也会返回到上一层的参数处，覆盖原来的参数，继续此函数之后未完成的函数动作，如果此函数执行完则跳出此层递归，继续返回上次未完成的函数处（递归调用处）。
理解一下递归的实质：

使用非递归的方法：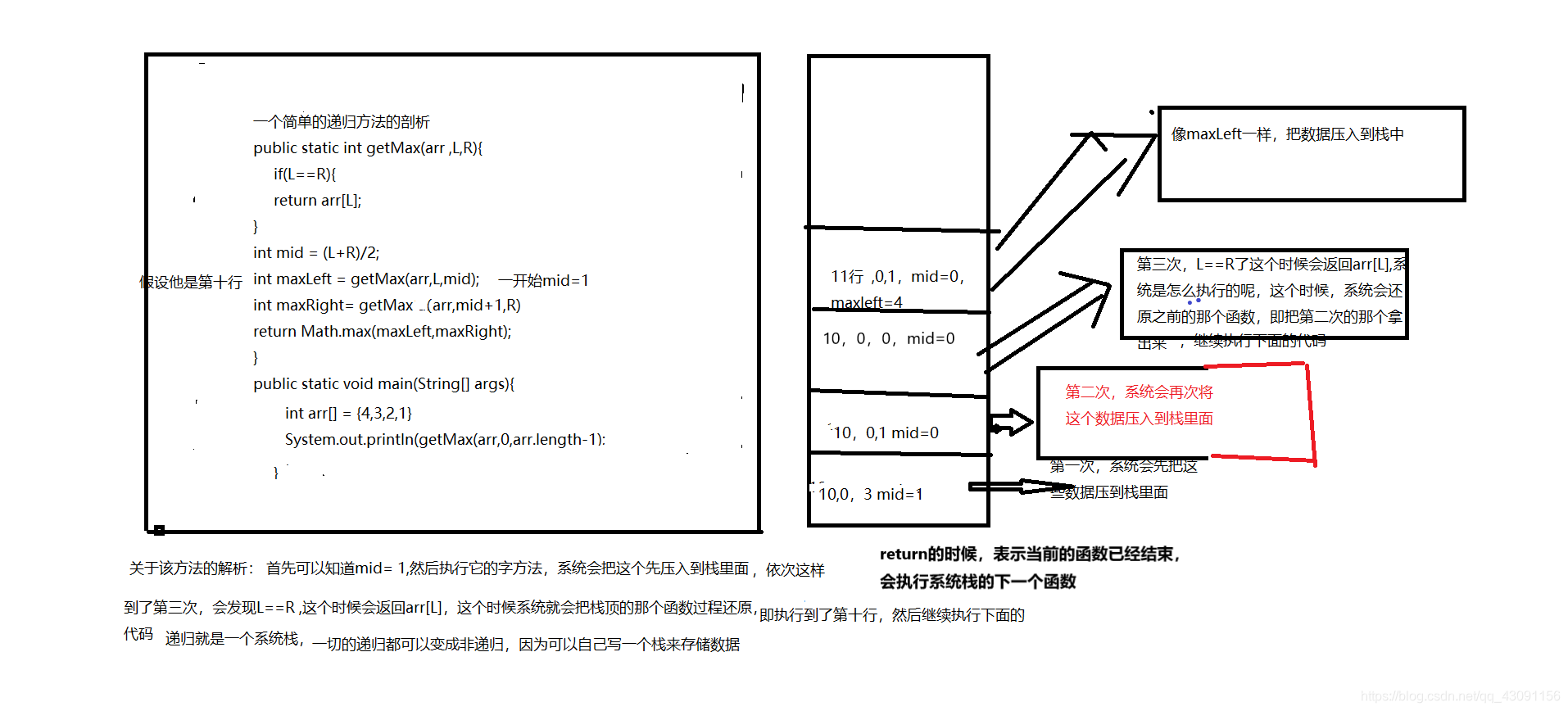
注意return：return的时候代表这个子函数已经执行完毕了，使用再执行的是下一个栈元素

import java.util.Stack;

public class Code_01_PreInPosTraversal {

	public static class Node {
		public int value;
		public Node left;
		public Node right;

		public Node(int data) {
			this.value = data;
		}
	}

	public static void preOrderRecur(Node head) { //递归的方式 先序遍历
		if (head == null) {
			return;
		}
		System.out.print(head.value + " ");
		preOrderRecur(head.left);
		preOrderRecur(head.right);
	}

	public static void inOrderRecur(Node head) { // 递归的方式 中序遍历
		if (head == null) {
			return;
		}
		inOrderRecur(head.left);
		System.out.print(head.value + " ");
		inOrderRecur(head.right);
	}

	public static void posOrderRecur(Node head) { //递归的方式 后序遍历
		if (head == null) {
			return;
		}
		posOrderRecur(head.left);
		posOrderRecur(head.right);
		System.out.print(head.value + " ");
	}

	public static void preOrderUnRecur(Node head) { //先序遍历 非递归
		System.out.print("pre-order: ");
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			stack.add(head);
			while (!stack.isEmpty()) { 
				head = stack.pop();
				System.out.print(head.value + " ");
				if (head.right != null) {  //先序遍历要先把右边的压入栈中
					stack.push(head.right);
				}
				if (head.left != null) {
					stack.push(head.left);
				}
			}
		}
		System.out.println();
	}

	public static void inOrderUnRecur(Node head) { //中序遍历 非递归
		System.out.print("in-order: ");
		if (head != null) {
			Stack<Node> stack = new Stack<Node>();
			while (!stack.isEmpty() || head != null) { //这个条件是当head在最高的节点时和head的左边为空时这个边界
				if (head != null) {  //把左边的节点依次压入栈中
					stack.push(head);
					head = head.left;
				} else {
					head = stack.pop(); //左边已经为空了，弹出，看右边有没有节点
					System.out.print(head.value + " ");
					head = head.right;
				}
			}
		}
		System.out.println();
	}

	public static void posOrderUnRecur1(Node head) { //后序遍历 非递归 使用两个栈
		System.out.print("pos-order: ");
		if (head != null) {
			Stack<Node> s1 = new Stack<Node>();
			Stack<Node> s2 = new Stack<Node>();//用来存放按后序排序好的二叉树
			s1.push(head);
			while (!s1.isEmpty()) {
				head = s1.pop();
				s2.push(head);
				if (head.left != null) {
					s1.push(head.left); //放到栈S2时刚好左子树的在右子树的上面
				}
				if (head.right != null) {
					s1.push(head.right);
				}
			}
			while (!s2.isEmpty()) {
				System.out.print(s2.pop().value + " ");
			}
		}
		System.out.println();
	}

	public static void posOrderUnRecur2(Node h) {  //使用一个栈
		System.out.print("pos-order: ");
		if (h != null) {
			Stack<Node> stack = new Stack<Node>();
			stack.push(h);
			Node c = null;
			while (!stack.isEmpty()) {
				c = stack.peek();//取出但不销毁，还是在原来的栈中
				if (c.left != null && h != c.left && h != c.right) {
					stack.push(c.left);
				} else if (c.right != null && h != c.right) { //防止一个节点被压入两次
					stack.push(c.right);
				} else {
					System.out.print(stack.pop().value + " ");
					h = c;
				}
			}
		}
		System.out.println();
	}

自己好好理解非递归，再自己敲一遍。