排序（三）：谁主沉浮——堆与堆排序

leetcode：https://leetcode-cn.com/problems/sort-an-array/

堆

定义&&性质

堆（heap）是计算机科学中一类特殊的数据结构的统称，通常是一个可以被看作是一棵树的数组对象。

定义：n 个元素的序列 {k1,k2,ki,…,kn} 当且仅当满足下关系时，称之为堆。$k_i\le k_{2i}$ 且 $k_i\le k_{2i+1}$ 或者 $k_i\ge k_{2i}$ 且 $k_i\ge k_{2i+1}$。若以一维数组存储此序列，并将数组视为完全二叉树，可知非叶子节点的值均不大于（或不小于）其左右子节点的值，堆顶元素（即二叉树的根）必为序列中 n 个元素的最小值。

性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

堆的建立方法

筛选法：下调

设堆共有 n 个节点，深度为 $lo{g}_2(n)$，设为 k。按照从下到上，从右到左的方法找到第一个非叶子节点 i（索引为 n/2）开始调整，使以该节点为根节点的子树为大顶堆。

调整策略：

• 取左右子节点中较大的一个与节点 i 比较；
• 若大于节点 i，父子交换值。若子节点仍有子节点（即节点 i 有孙子节点），则继续向下调整，确保以子节点为根节点的子树为大顶堆；
• 若小于节点 i，说明当前子树为大顶堆，结束。

根据树的相关性质，又有：

• 第 i 层最多有节点 $2^{i-1}$ 个；
• 非叶子节点的深度为 [0, k - 1] 即 [0, $lo{g}_{2}n-1$]
• 利用筛选法建堆，每层每个节点最多比较两次——父节点与两个子节点比较；
• 第 k - 1 层的节点最多下调一层，第 k - i 层的节点最多下调 i 层…以此类推。

所以，$S(k)={\sum }_{i=1}^{k-1}{2}^{i-1}\ast (k-i)\ast 2$，时间复杂度 $A(n)=O(n)$。

插入法：上浮

调整策略：

• 插入新元素时，只与它的父节点比较，无需和兄弟节点比较，上调一层，比较一次。二叉树第 i 层最多有 $2^{i-1}$ 个节点，每个节点最多上调 i - 1。

所以，$S(k)={\sum }_{i=2}^k{2}^{i-1}\ast (i-1)$，时间复杂度 $A(n)=O(nlogn)$。

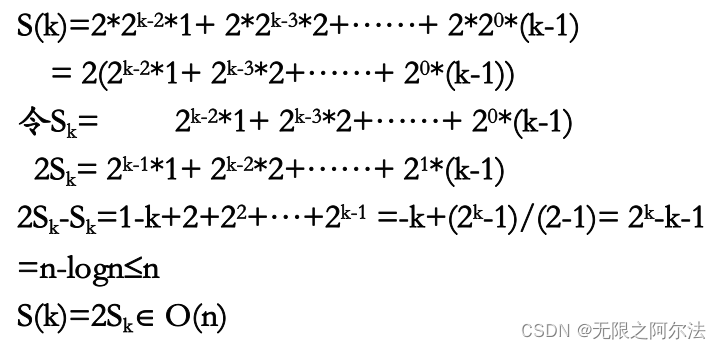
堆排序

过程

堆排序的基本思想是:

• 将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根节点。
• 将其与末尾元素进行交换，此时末尾元素为最大值。
• 然后将剩余 n-1 个元素重新构造成大顶堆，得到 n 个元素的次大值。如此反复执行，最终得到一个有序序列。

代码

筛选法建堆后堆排序：

class Solution {
    public int[] sortArray(int[] nums) {
        int len = nums.length;
        for(int i = len/2 - 1; i >= 0; i--){
            AdjustHeap(nums, i, len);
        }
        for(int j = len - 1; j > 0; j--){
            int temp = nums[j];
            nums[j] = nums[0];
            nums[0] = temp;
            AdjustHeap(nums, 0, j);
        }
        return nums;
    }

    public void AdjustHeap(int[] nums, int i, int size){
        int temp = nums[i];
        for(int child = 2*i+1; child < size; child = 2*child+1){
            // 选择较大的子节点进行比较
            if(child+1 < size && nums[child+1] > nums[child])
                child++;
            // 父节点小于子节点，向下继续调整
            if(temp < nums[child]){
                nums[i] = nums[child];
                i = child;
            }
            // 父节点大于子节点，符合大顶堆，跳出循环
            else
                break;
        }
        nums[i] = temp;
    }
}

插入法建堆后堆排序：

class Solution {
    int copy[] = new int[50000];  

    public int[] sortArray(int[] nums) {
        int len = nums.length;
        for(int i = 0; i < len; i++)
            BuildHeap(nums, i);
        for(int j = len - 1; j > 0; j--){
            swap(copy, j, 0);
            AdjustHeap(copy, 0, j);
        }
        for(int i = 0; i < len; i++)
            nums[i] = copy[i];
        return nums;
    }

    public void BuildHeap(int[] nums, int i){
        copy[i] = nums[i];
        // 子节点与父节点比较，如果大于父节点就上调
        // 父节点索引(i-1)/2
        while(i > 0 && copy[(i-1)/2] < copy[i]){
            swap(copy, (i-1)/2, i);
            i = (i-1)/2;
        }
    }

    public void AdjustHeap(int[] nums, int i, int size){
        /*
        代码见筛选法建堆
        */
    }
}

时间复杂度

堆排序的最优、最差和平均时间复杂度都为 $O(nlogn)$ ，是常用的排序算法中最稳定的排序方法，实验表明堆排序的稳定性优于归并排序。