8.1 二叉排序树 —— C语言实现

系列文章目录

参考船说系列——数据结构与算法中的第八章内容。

1. 二叉排序树
2. AVL树
3. 红黑树
4. B-树

---

---

前言

数据结构 = 结构定义 + 结构操作
结构操作是用来维护结构性质的

---

一、二叉排序树基础

二叉排序树（Binary Search Tree，BST）是一种二叉树，它具有以下性质：

1. 每个节点都有一个值，且节点的值都不相同。
2. 左子树中所有节点的值都小于该节点的值。
3. 右子树中所有节点的值都大于该节点的值。
4. 左右子树也分别为二叉排序树。

这些性质保证了二叉排序树的中序遍历是一个有序的序列。由于有序性，二叉排序树常被用于实现动态集合的数据结构，支持快速的查找、插入和删除操作。然而，如果插入的节点顺序不合理，可能导致二叉排序树退化成链表，影响其性能。

对于二叉排序树，平均情况下，查找、插入和删除操作的时间复杂度为O(log n)，其中n为树中节点的数量。但是，在最坏情况下，二叉排序树可能退化成一个高度为n的链表，导致这些操作的时间复杂度为O(n)。

中序遍历：

---

二、二叉排序树的操作

2.1 插入

1. 从根节点开始，比较要插入的值与当前节点的值。
   

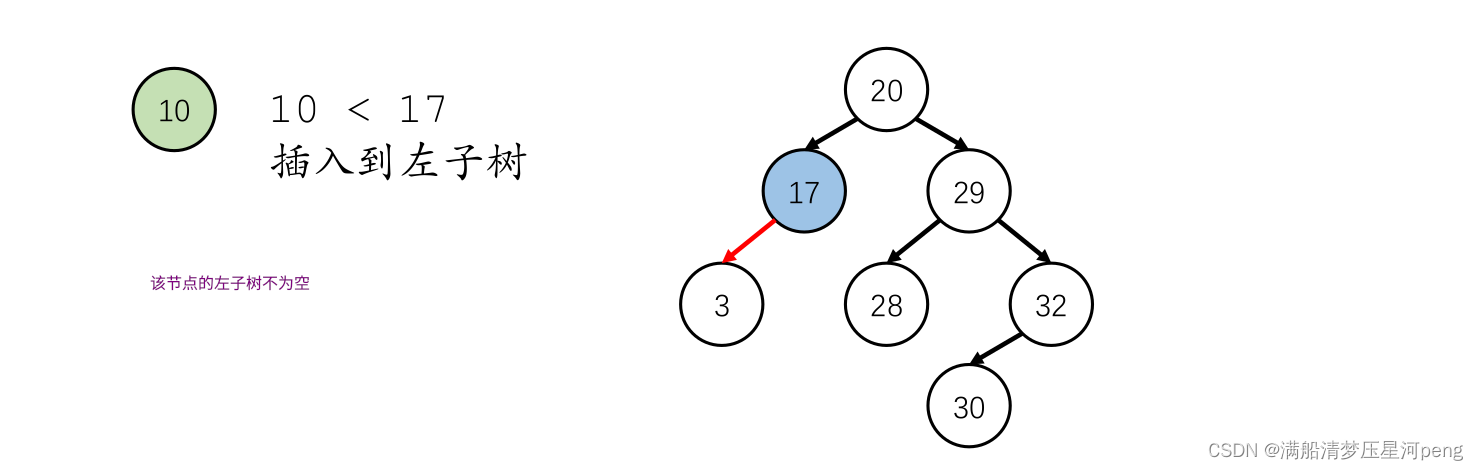
2. 如果要插入的值小于当前节点的值，并且当前节点的左子节点为空，则将新节点插入为当前节点的左子节点；如果不为空，则继续向左子树遍历。（递归子问题）
   

3. 如果要插入的值大于当前节点的值，并且当前节点的右子节点为空，则将新节点插入为当前节点的右子节点；如果不为空，则继续向右子树遍历。（递归子问题）
   

4. 重复步骤2和步骤3，直到找到合适的位置插入新节点。
   

2.2 删除

删除节点有几种情况要讨论：

1. 删除叶子节点
   直接删除即可

2. 删除出度为1的节点
   将其唯一子节点提升到要删除节点的位置

3. 删除出度为2的节点
   a. 20节点的前驱（前驱位置的出度只能是0或者1，因为前驱是之前节点中值最大的节点）替换20这个当前节点，这样20就成了它之前节点所在位置中的左子树中最大值的节点。这样删掉20节点就变成了一个删除出度为0或者1的问题了，解决办法就能参考前两种办法！！！
   b. 20节点的后继（后继位置的出度只能是0或者1，因为后继是之前节点中值最小的节点）替换20这个当前节点，这样20就成了它之前节点所在位置中的右子树中最小值的节点。这样删掉20节点就变成了一个删除出度为0或者1的问题了，解决办法就能参考前两种办法！！！

   有个容易找到前驱后继的方法：

   • 前驱是该节点的左子树一直往右，直到右节点为空的节点
   • 后继是该节点的右子树一直往左，直到左节点为空的节点

简单来说就是删除出度为2的节点，则可以选择将其右子树中最小的节点（后继）或左子树中最大的节点（前驱）替代要删除的节点，然后删除该最小或最大节点（变成了删除出度为0或者1的问题）。

---

三、代码演示

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define KEY(n) (n ? n->key : -1)

typedef struct Node{
	int key;
	struct Node *lchild, *rchild;
} Node;

Node *getNewNode(int key){
	Node *p = (Node *)malloc(sizeof(Node));
	p->key = key;
	p->lchild = p->rchild = NULL;
	return p;
}

Node *insert(Node *root, int key){
	if (root == NULL) return getNewNode(key);
	if (key == root->key) return root; //重复的值不再插入
	if (key < root->key) root->lchild = insert(root->lchild, key);
	else root->rchild = insert(root->rchild, key);
	return root;   //返回根节点的地址
}

Node *predecessor(Node *root){
	Node *temp = root->lchild;
	while (temp->rchild) temp = temp->rchild;
	return temp;
}

Node *erase(Node *root, int key){
	if (root == NULL) return root;
	if (key < root->key) root->lchild = erase(root->lchild, key);
	else if (key > root->key) root->rchild = erase(root->rchild, key);
	else {
		if (root->lchild == NULL && root->rchild == NULL){
			free(root);
			return NULL;
		}else if (root->lchild == NULL || root->rchild == NULL){
			Node *temp = root->lchild ? root->lchild : root->rchild;
			free(root);
			return temp;
		}else {
			Node *temp = predecessor(root); //找到当前节点的前驱
			root->key = temp->key;
			root->lchild = erase(root->lchild, temp->key);
		}
	}
	return root;
}

void clear(Node *root){
	if (root == NULL) return;
	clear(root->lchild);
	clear(root->rchild);
	clear(root);
	return;
}

void output(Node *root){
	if (root == NULL) return;
	printf("(%d ; %d, %d)\n", 
			KEY(root), 
			KEY(root->lchild), 
			KEY(root->rchild)
	);
	output(root->lchild);
	output(root->rchild);
	return;
}

void in_order(Node *root){
	if (root == NULL) return;
	in_order(root->lchild);
	printf("%d ", root->key);
	in_order(root->rchild);
	return;
}


int main(){
	srand(time(0));
	#define MAX_OP 10
	Node *root = NULL;
	for (int i = 0; i < MAX_OP; i++){
		int key = rand() % 100;
		printf("insert key %d to BST\n", key);
		root = insert(root, key); //完成插入操作后新的BST根节点的地址
	}

	output(root);
	printf("in_order : ");
	in_order(root);
	printf("\n");
	int x;
	while (~scanf("%d", &x)){
		printf("erase %d from BST\n", x);
		root = erase(root, x);
		in_order(root);
		printf("\n");
	}
	return 0;
}

注意：在实际工程中，使用二叉排序树一般不会重复的key值，所以重复的数无须插入。

输出结果：

---

总结

1. 二叉排序树又称二叉搜索树，性质，中序遍历排序。
2. 插入操作，按照其结构性质做一个递归即可。
3. 删除操作，又分三种情况，最后一种情况可以转换成为前两种情况来实现。

参考文献

1. 船说系列——数据结构与算法