问题描述
有三对夫妻要过河,约束条件是,根据法律,任一女子不得在其丈夫不在场的情况下与另外男子在一起,问此时这三对夫妻能否过河?
解法分析
这里就直接使用书上的解法,不多做描述


代码思路
根据解法看出,下层的解法与上层有关,这显然是一个简单的dfs,先dfs一遍求出最小值,然后dfs一遍输出路径(这里可以优化)。时间复杂度大概是O(n2)级别。
代码样例
#include <iostream>
#include <cmath>
#include <set>
#include <string>
#include <vector>
#include <cstdio>
#define NUM_MALE 6 // 左岸初始男的数量
#define NUM_FMALE 6 // 左岸初始女的数量
#define NUM_BOAT 2
struct node
{
int n, m, sg;
bool operator<(const node& b) const
{
if (n != b.n) return n < b.n;
else if (m != b.m) return m < b.m;
else return sg < b.sg;
}
};
std::set<node> st;
std::set<node> st_print;
std::vector<node> arr_print;
// 用于求最小值的dfs
int dfs(int male, int fmale, int pos)
{
if (male == 0 && fmale == 0)
return pos - 1;
int ans = INT_MAX;
for (int i = 0; i <= NUM_BOAT; i ++)
for (int j = 0; j <= NUM_BOAT; j ++)
{
int nm = i + j;
int sg = pos % 2 == 0 ? 1 : -1;
if (nm >= 1 && nm <= 2)
{
int new_male = male + sg * i;
int new_fmale = fmale + sg * j;
if (st.count({new_male, new_fmale, sg}) == 0
&& new_male >= new_fmale
&& new_fmale <= NUM_FMALE
&& new_male <= NUM_MALE
&& new_male >= 0
&& new_fmale >= 0)
{
st.insert({new_male, new_fmale, sg});
ans = std::min(ans, dfs(new_male, new_fmale, pos + 1));
}
}
}
return ans;
}
void printArr()
{
int siz = arr_print.size();
std::vector<node>& arr = arr_print;
printf("(%d, %d)-->", NUM_MALE, NUM_FMALE);
for (int i = 0; i < siz; i ++)
{
printf("(%d, %d)", arr[i].n, arr[i].m);
if (i != siz - 1) printf("-->");
}
}
// 输出用的dfs
void printDfs(int male, int fmale, int pos, const int minnum)
{
if (male == 0 && fmale == 0 && pos == minnum + 1)
{
printArr();
}
int ans = INT_MAX;
for (int i = 0; i <= NUM_BOAT; i ++)
for (int j = 0; j <= NUM_BOAT; j ++)
{
int nm = i + j;
int sg = pos % 2 == 0 ? 1 : -1;
if (nm >= 1 && nm <= 2)
{
int new_male = male + sg * i;
int new_fmale = fmale + sg * j;
if (st_print.count({new_male, new_fmale, sg}) == 0
&& new_male >= new_fmale
&& new_fmale <= NUM_FMALE
&& new_male <= NUM_MALE
&& new_male >= 0
&& new_fmale >= 0)
{
st_print.insert({new_male, new_fmale, sg});
arr_print.push_back({new_male, new_fmale, sg});
printDfs(new_male, new_fmale, pos + 1, minnum);
arr_print.pop_back();
}
}
}
}
int main(int argc, char** argv)
{
st.insert({NUM_MALE, NUM_FMALE, 1});
int minnum = dfs(NUM_MALE, NUM_FMALE, 1);
std::cout << "最少要" << minnum << "步骤" << '\n';
std::cout << "下列是最短路径 : " << '\n';
std::cout << "左岸的男女变化,格式为(男,女)" << '\n';
st_print.insert({NUM_MALE, NUM_FMALE, 1});
printDfs(NUM_MALE, NUM_FMALE, 1, minnum);
return 0;
}
结果分析
当男3女3结果为:

当男6女6结果为:
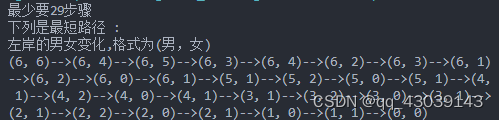
其他结果大家自己去试试就行
优化想法
这里提供一个不成熟的优化想法。根据规律可看出无论怎么样都是把女先全部运过去,然后一个个去减少男的数量。按理来说是可以用排列组合把公式推出来的,可能可以把时间优化成O(1) ? 不太确定。如果有人成功优化的话,可以在评论区告诉一下博主。QAQ







 文章介绍了一个关于三对夫妻过河的问题,其中约束条件是任何女子不能在没有丈夫陪同的情况下与其他男子在一起。解决此问题采用的是深度优先搜索(DFS)算法,首先通过DFS找到最小步数,然后再进行一次DFS以输出解决方案的路径。代码示例展示了如何实现这一过程,时间复杂度大约为O(n^2)。文章最后提出了可能的优化思路,即尝试通过排列组合推导出公式以提高效率。
文章介绍了一个关于三对夫妻过河的问题,其中约束条件是任何女子不能在没有丈夫陪同的情况下与其他男子在一起。解决此问题采用的是深度优先搜索(DFS)算法,首先通过DFS找到最小步数,然后再进行一次DFS以输出解决方案的路径。代码示例展示了如何实现这一过程,时间复杂度大约为O(n^2)。文章最后提出了可能的优化思路,即尝试通过排列组合推导出公式以提高效率。
















 230
230

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








