2019-05-21 图进阶

割顶的定义：

对于无向图G，如果删除某个点u之后，联通分量数量增加，则称u为图的割顶。

DFS时标记每个点遍历的次序为dfn
规定low(u)为u及其后代所能连回的最早祖先的dfn值
如：

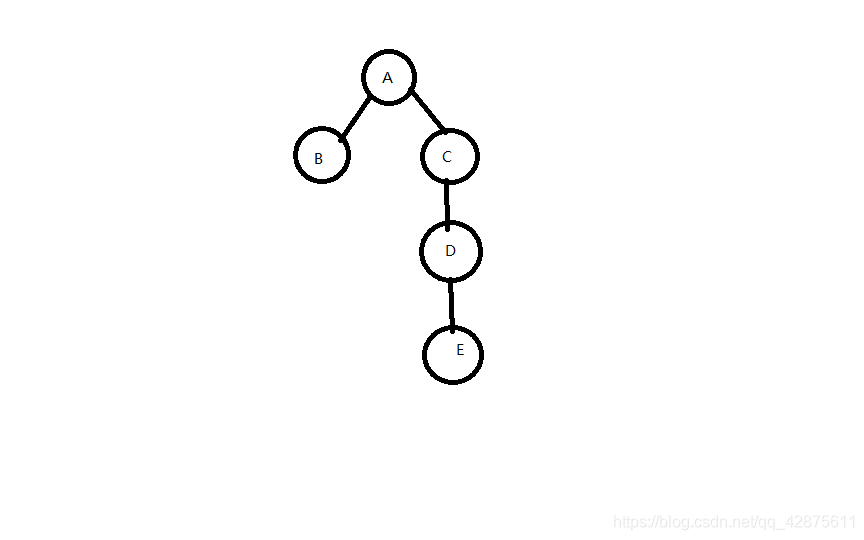
该图中，
A B C D E
dfn 1 2 3 4 5
low 1 2 3 3 3

因为e有一条边可连回c（图上未标），所以c，d，e三点的low值都为c的dfn值——3

求割顶代码：

vector<int> G[maxn];
int vis[maxn],low[maxn],dfn[maxn];
int tmpdfn=0;
void dfs(int u){//开始递归 
	vis[u]=1;//标志已经遍历 
	low[u]=dfn[u]=++tmpdfn;//现将low和dfn的值设为本身 
	for(int i=0;i<G[u].size();i++){//开始 
		int v=G[u][i];
		if(!vis[v]){//回退的时候，找祖先节点u能达到的较小的low值 
			dfs(v);
			low[u]=min(low[u],low[v]);
		}
		else{//这时候i是u的祖先先点，且这是一条回边 
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(G[u].size()>1&&low[u]==dfn[u])//标记 
		ans[++cnt]=u;
	return ;//返回 
}

Triangle LOVE

这道题有两种算法：
1.暴力搜索，判断是否有“三角恋”
2.利用拓扑算法，易证只要有环，必定有三角恋（任意两点必有A love B，但B dislike A），所以只要找到图中有没有环就行了

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=2010;
int n,x[maxn],t; 
char str[maxn][maxn];
int main(){
    scanf("%d",&t);
    for(int i=1;i<=t;i++){
        scanf("%d",&n);
        int flag=0;
        memset(x,0,sizeof(x));  //将所有的节点入度初始化为0
        for(int i=0;i<n;i++){
            scanf("%s",str[i]);
            for(int j=0;j<n;j++)
                if(str[i][j]=='1')  //如果i喜欢j,则把j的入度加1
                    x[j]++;
        }
        for(int i=0;i<n;i++){
        	int j;
            for(j=0;j<n;j++)
                if(x[j]==0)     //找出入度为0的节点
                    break;
            if(j==n){       //任何一个节点的入度都不为0，说明存在环了，则必有三角恋
                flag=1;
                break;
            }
			else{
                x[j]--; //除去当前结点
                for(int k=0;k<n;k++)    //把从这个节点出发的引起的节点的入度都减去1
                    if(str[j][k]=='1')
                        x[k]--;
            }
        }
        if(flag)
            printf("Case #%d: Yes\n",i);
        else
            printf("Case #%d: No\n",i);
    }
    return 0;
}