【李沐AI自学】线性神经网络

线性回归

在机器学习领域中的⼤多数任务通常都与预测（prediction）有关。当我们想预测⼀个数值时，就会涉及到回归问题。常⻅的例⼦包括：预测价格（房屋、股票等）、预测住院时间（针对住院病⼈等）、预测需求（零售销量等）。但不是所有的预测都是回归问题。在后⾯的章节中，我们将介绍分类问题。分类问题的⽬标是预测数据属于⼀组类别中的哪⼀个。

线性回归基本元素

为了解释线性回归，我们举⼀个实际的例⼦：我们希望根据房屋的⾯积（平⽅英尺）和房龄（年）来估算房屋价格（美元）。为了开发⼀个能预测房价的模型，我们需要收集⼀个真实的数据集。这个数据集包括了房屋的销售价格、⾯积和房龄。在机器学习的术语中，该数据集称为训练数据集（training data set）或训练集（training set）。每⾏数据（⽐如⼀次房屋交易相对应的数据）称为样本（sample），也可以称为数据点（data point）或数据样本（data instance）。我们把试图预测的⽬标（⽐如预测房屋价格）称为标签（label）或⽬标（target）。预测所依据的⾃变量（⾯积和房龄）称为特征（feature）或协变量（covariate）。

由于平⽅误差函数中的⼆次⽅项，估计值yˆ(i)和观测值y(i)之间较⼤的差异将导致更⼤的损失。为了度量模型在整个数据集上的质量，我们需计算在训练集n个样本上的损失均值（也等价于求和）。

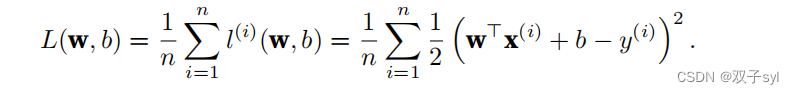
在训练模型时，我们希望寻找⼀组参数（w∗, b∗），这组参数能最⼩化在所有训练样本上的总损失。如下式：



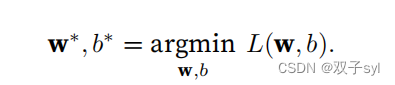
线性回归，前向传播的是计算得到的y‘值，然后根据y’-y计算loss，然后反向传播，每一个特征（相当于邻接矩阵的那些列）的loss分别对w和b求偏导，得到每一个特征的梯度，也就是3.1.10式子，以此来更新w和b。

⽮量化加速

在训练我们的模型时，我们经常希望能够同时处理整个⼩批量的样本。为了实现这⼀点，需要我们对计算进⾏⽮量化，从⽽利⽤线性代数库，⽽不是在Python中编写开销⾼昂的for循环。

%matplotlib inline
import math
import time
import numpy as np
import torch
from d2l import torch as d2l
	n = 10000
	a = torch.ones(n)
	b = torch.ones(n)

由于在本书中我们将频繁地进⾏运⾏时间的基准测试，所以我们定义⼀个计时器：

class Timer: #@save
"""记录多次运⾏时间"""
	def __init__(self):
		self.times = []
		self.start()
	def start(self):
"""启动计时器"""
	self.tik = time.time()
	def stop(self):
"""停⽌计时器并将时间记录在列表中"""
	self.times.append(time.time() - self.tik)
		return self.times[-1]
	def avg(self):
"""返回平均时间"""
		return sum(self.times) / len(self.times)
	def sum(self):
"""返回时间总和"""
		return sum(self.times)
	def cumsum(self):
"""返回累计时间"""
		return np.array(self.times).cumsum().tolist()

现在我们可以对⼯作负载进⾏基准测试。
⾸先，我们使⽤for循环，每次执⾏⼀位的加法。

	c = torch.zeros(n)
	timer = Timer()
	for i in range(n):
		c[i] = a[i] + b[i]
		f'{
     
     timer.stop():.5f} sec'
		'0.08976 sec'

或者，我们使⽤重载的+运算符来计算按元素的和。

timer.start()
d = a + b f'{
     
     timer.stop():.5f} sec'
'0.00027 sec'

正态分布和平方损失

接下来，我们通过对噪声分布的假设来解读平⽅损失⽬标函数。
正态分布和线性回归之间的关系很密切。正态分布（normal distribution），也称为⾼斯分布（Gaussian
distribution），最早由德国数学家⾼斯（Gauss）应⽤于天⽂学研究。简单的说，若随机变量x具有均值µ和⽅差σ2（标准差σ），其正态分布概率密度函数如下：

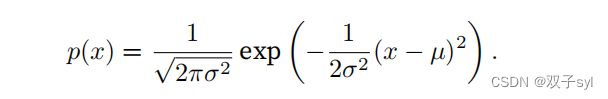
下⾯我们定义⼀个Python函数来计算正态分布。

def normal(x, mu, sigma):
		p = 1 / math.sqrt(2 * math.pi * sigma**2)
		return p * np.exp(-0.5 / sigma**2 * (x - mu)**2)

我们现在可视化正态分布。

# 再次使⽤numpy进⾏可视化
x = np.arange(-7, 7, 0.01) # 均值和标准差对
params = [(0, 1), (0, 2), (3, 1)]
d2l.plot(x, [normal(x, mu, sigma) for mu, sigma in params], xlabel='x',
ylabel='p(x)', figsize=(4.5, 2.5),
legend=[f'mean {
     
     mu}, std {
     
     sigma}' for mu, sigma in params])

线性回归的从零开始实现

⽣成数据集

为了简单起⻅，我们将根据带有噪声的线性模型构造⼀个⼈造数据集。我们的任务是使⽤这个有限样本的数据集来恢复这个模型的参数。我们将使⽤低维数据，这样可以很容易地将其可视化。在下⾯的代码中，我们⽣成⼀个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。我们的合成数据集是⼀个矩阵X ∈ R1000×2。我们使⽤线性模型参数w = [2, −3.4]⊤、b = 4.2 和噪声项ϵ⽣成数据集及其标签：
你可以将ϵ视为模型预测和标签时的潜在观测误差。在这⾥我们认为标准假设成⽴，即ϵ服从均值为0的正态分布。为了简化问题，我们将标准差设为0.01。下⾯的代码⽣成合成数据集。

%matplotlib inline
import random
import torch
from d2l import torch as d21
def synthetic_data(w, b, num_examples): #@save
    """生成 y = Xw + b + 噪声。"""
    X=torch.normal(0,1,(num_examples,len(w)))
    y=torch.matmul(X,w)+b#matmul所以矩阵向量乘法都可以通过广播机制实现
    y+=torch.normal(0,0.01,y.shape)
    return X,y.reshape(-1,1)
torch.normal(2,3,size=(1,4))
# tensor([[-1.3987, -1.9544,  3.6048,  0.7909]])
true_w = torch.tensor([2, -3.4])
true_b = 4.2
features,labels=synthetic_data(true_w,true_b,1000)
features,labels
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);

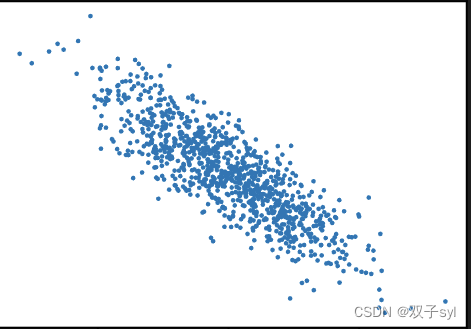
读取数据集

回想⼀下，训练模型时要对数据集进⾏遍历，每次抽取⼀⼩批量样本，并使⽤它们来更新我们的模型。由于这个过程是训练机器学习算法的基础，所以有必要定义⼀个函数，该函数能打乱数据集中的样本并以⼩批量⽅式获取数据。在下⾯的代码中，我们定义⼀个data_iter函数，该函数接收批量⼤⼩、特征矩阵和标签向量作为输⼊，⽣成⼤⼩为batch_size的⼩批量。每个⼩批量包含⼀组特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))#0-999的数组列表
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)#打乱顺序
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])#tensor([993, 616, 127, 509, 119, 167, 648, 486, 907,  27])前十个
        yield features[batch_indices], labels[batch_indices]
    #yield可以理解为一个return操作，但是和return又有很大的区别，执行完return，当前函数就终止了，函数内部的所有数据，所占的内存空间，全部都没有了。
    #而yield在返回数据的同时，还保存了当前的执行内容，当你再一次调用这个函数时，他会找到你在此函数中的yield关键字，然后从yield的下一句开始执行。

通常，我们利⽤GPU并⾏运算的优势，处理合理⼤⼩的“⼩批量”。每个样本都可以并⾏地进⾏模型计算，且每个样本损失函数的梯度也可以被并⾏计算。GPU可以在处理⼏百个样本时，所花费的时间不⽐处理⼀个样本时多太多。我们直观感受⼀下⼩批量运算：读取第⼀个⼩批量数据样本并打印。每个批量的特征维度显⽰批量⼤⼩和输⼊特征数。同样的，批量的标签形状与batch_size相等。

batch_size = 10
for X, y in data_iter