Average UVA - 1451 数形结合

题目链接

大意：

给定一个长度为n的01串，选一个长度至少为L的连续子串，使得子串中数字的平均值最大。

如果有多解，子串长度应尽量小；如果仍有多解，起点编号尽量小。序列中的字符编号为1～n，因此[1,n]就是完整的字符串。1≤n≤100000，1≤L≤1000。例如，对于如下长度为17的序列00101011011011010，如果L=7，最大平均值为6/8（子序列为[7,14]，其长度为8）；如果L=5，子序列[7,11]的平均值最大，为4/5。

【分析】
先求前缀和Si=A1+A2+…+Ai（规定S0=0），然后令点Pi=(i, Si)，则子序列i～j的平均值为(Sj-Si-1)/(j-i+1)，也就是直线P(i-1)Pj的斜率。这样可得到主算法：从小到大枚举t，快速找到t'≤t-L，使得Pt'Pt斜率最大。注意题目中的Ai都是0或1，因此每个Pi和上一个P(i-1)相比，都是x加1，y不变或者加1。

对于给定的t，要找的点Pt'在Pt的左边。假设有3个候选点Pi、Pj、Pk，下标满足i<j<k<t，并且3个点成上凸形状（Pj为上凸点）。假设Pt的x坐标为x0，根据定义，Pt的y坐标一定不小于Pk的y坐标，因此Pt一定位于A、B、C3条线段/射线之一，如图8-16所示。

1. 当Pt在射线A上时，Pk比Pj好（即PkPt的斜率比PjPt的斜率大，后同）。
2. 当Pt在线段B上时，Pi比Pj好。
3. 当Pt在线段C上时，Pi和Pk都比Pj好。

换句话说，只要出现上凸的情况，上凸点一定可以忽略。假设已经有了一些下凸点，现在又加入了一个点，可能会使一些已有的点变为上凸点，这时就应当将这些上凸点删除。由于被删除的点总是原来的下凸点中最右边的若干个连续
点，所以可以用栈来实现，如图8-17所示。

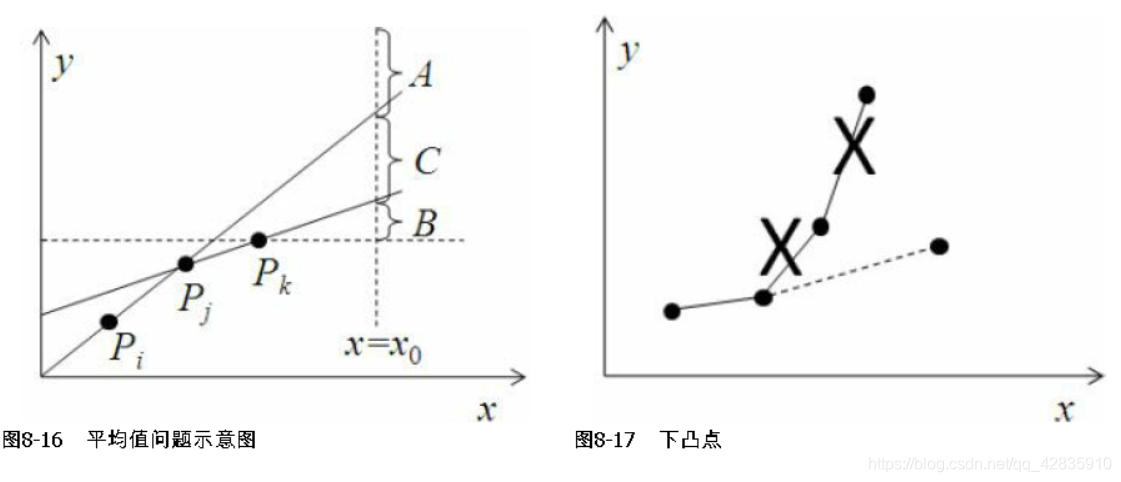
 得到下凸线之后，对于任何一个点Pt来说，最优点Pt'都在切点，如图8-18所示。

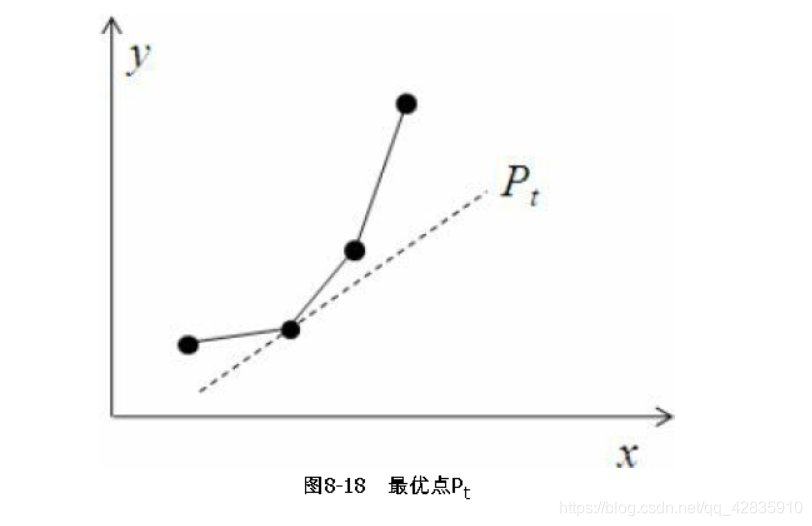
如何求切点呢？随着t的增大，斜率也是越来越大，所以每次求出的t'只会增大，不会减小。因此每次增加到斜率变小时停下来即可。时间复杂度为O(n) 

#include<cstdio>
using namespace std;
const int maxn = 100000 + 5;
int n, L;
char s[maxn];
int sum[maxn], p[maxn]; // average of i~j is (sum[j]-sum[i-1])/(j-i+1)
// compare average of x1~x2 and x3~x4
int compare_average(int x1, int x2, int x3, int x4) {
  return (sum[x2]-sum[x1-1]) * (x4-x3+1) - (sum[x4]-sum[x3-1]) * (x2-x1+1);
}

int main() {
  int T;
  scanf("%d", &T);
  while(T--) {
    scanf("%d%d%s", &n, &L, s+1);
    sum[0] = 0;
    for(int i = 1; i <= n; i++) sum[i] = sum[i-1] + s[i] - '0';
    int ansL = 1, ansR = L;
    // p[i..j) is the sequence of candidate start points
    int i = 0, j = 0;
    for (int t = L; t <= n; t++) { // end point
      while (j-i > 1 && compare_average(p[j-2], t-L, p[j-1], t-L) >= 0) j--; // remove concave points
      p[j++] = t-L+1; // new candidate
      while (j-i > 1 && compare_average(p[i], t, p[i+1], t) <= 0) i++; // update tangent point
      // compare and update solution
      int c = compare_average(p[i], t, ansL, ansR);
      if (c > 0 || c == 0 && t - p[i] < ansR - ansL) {
        ansL = p[i]; ansR = t;
      }
    }
    printf("%d %d\n", ansL, ansR);
  }
  return 0;
}