数据结构——二叉树

二叉树

二叉树的定义

二叉树在一般的树上加了两个限制条件：

• 每个结点最多只有两个子树
• 子树有左右之分，不能颠倒

二叉树的形态

• 空二叉树
• 只有根结点
• 只有左子树，右子树为空
• 只有右子树，左子树为空
• 既有左子树，又有右子树

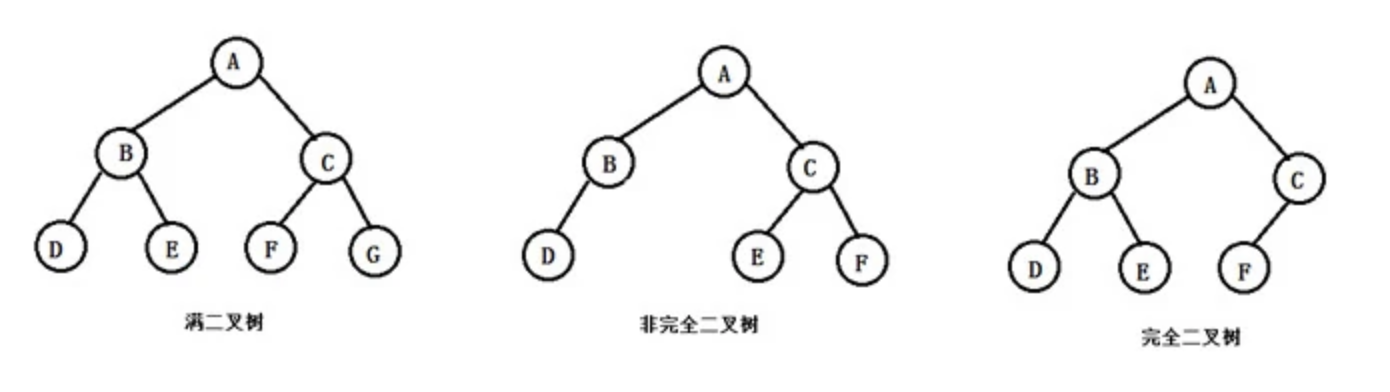
满二叉树、完全二叉树以及非完全二叉树

• 满二叉树：所有的分支结点都有左、右子节点，并且所有叶子结点都集中在最下层的二叉树。
• 完全二叉树：对一棵深度为k、有n个结点二叉树编号后，各节点的编号与深度为k的满二叉树相同位置的结点的编号相同，这颗二叉树就被称为完全二叉树
• 非完全二叉树：没有满足完全二叉树中的条件的二叉树

二叉树的主要性质

• 非空二叉树上叶子结点数等于双分支结点（有两个分支的结点）数加1

• 总结点数 = 叶子结点数 + 单分支结点数 + 双分支结点数 = 单分支结点数 + 2*双分支结点数

• 总分支数 = 总结点数 - 1 （此性质对所有树都成立，并非只是二叉树）

• 空指针数 = 所有结点数 + 1

• 二叉树第i层最多有**2^(i-1)**个结点，其中i>=1

• 深度为k的二叉树最多有2^k - 1个结点

• 有n个结点的完全二叉树，对各结点从上到下、从左到右编号。若i为某结点a的编号（范围1~n）。

  • 若i不等于1，则a父结点的编号为不超过(i/2)的最大整数
  • 若2i<=n,则a左儿子的编号为2i; 若2i>n，则a无左儿子
  • 若2i+1<=n,则a的右儿子编号为2i+1;若2i+1>n，则a无右儿子

• 给定n个结点，能构成二叉树种数如下
  $$C_{2n}^n/(n+1)$$

• 具有n个结点的二叉树深度如下
  $$\lfloor lo{g}_{2}n\rfloor +1$$

二叉树的储存结构

顺序储存结构

顺序储存结构用一个数组来存放一棵二叉树，这种方式最适合完全二叉树

定义如下

int Tree[1024];	//顺序结构的二叉树

若某结点编号为i，且存在左儿子和右儿子，则他们分别对应

Tree[i*2];	//左儿子
Tree[2*i+1];	//右儿子

链式储存结构

定义如下

typedef struct _BtTree{
    
    int data;
    struct _BtTree *leftchild;
    struct _BtTree *rightchild;
    
}BtTree;