卡尔曼滤波（Kalman Filter）核心原理与应用指南

卡尔曼滤波（Kalman Filter）核心原理与应用指南

1. 背景

卡尔曼滤波（Kalman Filter）是一种递归状态估计算法，由鲁道夫·卡尔曼（Rudolf Kalman）于1960年提出，最初用于解决阿波罗飞船的导航问题。其核心目标是在存在不确定性的动态系统中，融合多源噪声数据，实现最优状态估计。

历史背景与设计动机：
在航天、制导等场景中，传感器（如陀螺仪、加速度计）的测量值存在噪声（Noise），且系统本身受随机扰动影响。传统滤波方法（如移动平均）无法处理动态系统的状态变化。例如，火箭轨迹预测需同时结合运动模型（物理规律）和实时观测数据，但两者均不完美。卡尔曼滤波通过概率框架将模型预测（Prediction）与观测更新（Update）融合，得到比单一数据源更精确的估计结果。

示例：GPS 定位时，设备移动速度与卫星信号存在噪声。若仅依赖卫星数据，定位点会跳跃；仅用运动模型会累积误差。卡尔曼滤波将两者结合，输出平滑轨迹。

---

2. 技术原理

基于贝叶斯概率框架和最小均方误差（MMSE）准则，通过“预测-更新”循环迭代优化估计值。

系统用两个方程描述：

• 状态方程（State Equation）：
  $${\mathbf{x}}_k={\mathbf{F}}_k{\mathbf{x}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k+{\mathbf{w}}_k$$
  其中 ${\mathbf{x}}_{\mathbf{k}}$ 是状态向量，${\mathbf{F}}_{\mathbf{k}}$ 是状态转移矩阵，${\mathbf{u}}_{\mathbf{k}}$ 是控制输入，${\mathbf{w}}_{\mathbf{k}}\sim \mathcal{N}(0,{\mathbf{Q}}_{\mathbf{k}})$ 是过程噪声。

• 观测方程（Observation Equation）：
  $${\mathbf{z}}_k={\mathbf{H}}_k{\mathbf{x}}_k+{\mathbf{v}}_k$$
  其中 ${\mathbf{z}}_{\mathbf{k}}$ 是观测值，${\mathbf{H}}_{\mathbf{k}}$ 是观测转移矩阵，${\mathbf{v}}_{\mathbf{k}}\sim \mathcal{N}(0,{\mathbf{R}}_{\mathbf{k}})$ 是观测噪声。

• 状态估计方程与观测估计方程：
  $$\begin{array}{c}\begin{array}{rl}{\hat{\mathbf{x}}}_k& ={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k\\ {\hat{\mathbf{z}}}_k& ={\mathbf{H}}_k{\hat{\mathbf{x}}}_k\end{array}\end{array}$$

卡尔曼滤波主要分为预测与更新阶段：

预测阶段（Prior Estimate）

基于 $k-1$ 时刻的后验估计，预测 $k$ 时刻的状态和不确定性（通过协方差描述不确定性）：
$$\begin{array}{rl}\text{状态预测:}& {\hat{\mathbf{x}}}_k^{-}={\mathbf{F}}_k{\hat{\mathbf{x}}}_{k-1}+{\mathbf{B}}_k{\mathbf{u}}_k\\ \text{协方差预测:}& {\mathbf{P}}_k^{-}={\mathbf{F}}_k{\mathbf{P}}_{k-1}^{+}{\mathbf{F}}_k^T+{\mathbf{Q}}_k\end{array}$$

物理意义：

• 式 (1)：用系统模型 ${\mathbf{F}}_k$ 和控制输入${\mathbf{u}}_k$ 预测新状态。
• 式 (2)：预测的不确定性 ${\mathbf{P}}_k$ 来自模型传播 ${\mathbf{F}}_k{\mathbf{P}}_{k-1}^{+}{\mathbf{F}}_k^T$ 和过程噪声协方差矩阵 ${\mathbf{Q}}_k$。

$\mathbf{P}$ 是估计误差的协方差矩阵（Estimation Error Covariance Matrix）：
$${\mathbf{P}}_k=\text{cov}({\mathbf{e}}_k)=E\left[{\mathbf{e}}_k{\mathbf{e}}_k^T\right]$$
其中：

• ${\mathbf{e}}_k={\mathbf{x}}_k-{\hat{\mathbf{x}}}_k$ 是 状态估计误差（真实状态 ${\mathbf{x}}_k$ 与估计值 ${\hat{\mathbf{x}}}_k$ 的差值）。
• $\text{cov}(\cdot )$ 表示协方差矩阵。
• $E[\cdot ]$ 表示期望值（概率平均）。

更新阶段（Posterior Estimate）

获得测量 ${\mathbf{z}}_k$ 后，融合预测与测量，计算当前的状态估计：
$$\begin{array}{rl}\text{卡尔曼增益:}& {\mathbf{K}}_k={\mathbf{P}}_k{\mathbf{H}}_k^T({\mathbf{H}}_k{\mathbf{P}}_k{\mathbf{H}}_k^T+{\mathbf{R}}_k{)}^{-1}\\ \text{状态更新:}& {\hat{\mathbf{x}}}_k^{+}={\hat{\mathbf{x}}}_k^{-}+{\mathbf{K}}_k({\mathbf{z}}_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_k^{-})\\ \text{协方差更新:}& {\mathbf{P}}_k^{+}=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{H}}_k){\mathbf{P}}_k^{-}\end{array}$$

物理意义：

• 式 (3)：计算权重 ${\mathbf{K}}_k$。分母 ${\mathbf{H}}_k{\mathbf{P}}_k^{-}{\mathbf{H}}_k^T+{\mathbf{R}}_k$ 是新息协方差（预测与测量的联合不确定性）。
• 式 (4)：用 ${\mathbf{K}}_k$ 加权修正预测值。$({\mathbf{z}}_k-{\mathbf{H}}_k{\hat{\mathbf{x}}}_k^{-})$ 称为新息（测量残差）。
• 式 (5)：更新后的不确定性 ${\mathbf{P}}_k^{+}$ 因融合信息而减小 $(\mathbf{I}-{\mathbf{K}}_k\mathbf{H}$ 的作用）。

关键直观理解

1. 卡尔曼增益 ${\mathbf{K}}_k$：

   • 若传感器精度高( $\mathbf{R}\to 0$），则 ${\mathbf{K}}_k\approx {\mathbf{H}}_k^{-1}$ → 更信任测量。
   • 若模型精度高（${\mathbf{P}}_k^{-}\to 0$），则 ${\mathbf{K}}_k\to 0$ → 更信任预测。

2. 协方差更新：
   ${\mathbf{P}}_k^{+}$ 总是 ≤ ${\mathbf{P}}_k^{-}$（矩阵半正定序），表明融合后不确定性降低。

3. 最优性：
   在线性高斯系统中，卡尔曼滤波给出最小均方误差估计（MMSE）。

注：实际应用中需初始化 ${\hat{\mathbf{x}}}_0^{+}$ 和 ${\mathbf{P}}_0^{+}$，并循环执行预测-更新。

---

3. 功能特征

核心功能 1：多源数据融合（Sensor Fusion）

场景：自动驾驶中融合雷达（准确测距但噪声大）和摄像头（高分辨率但受光照影响）。
卡尔曼滤波将两者数据加权融合，输出鲁棒性更高的目标位置估计。

核心功能 2：动态噪声过滤（Dynamic Noise Filtering）

场景：无人机姿态估计。陀螺仪高频噪声小但存在漂移，加速度计低频噪声大但无漂移。
卡尔曼滤波结合两者优势，实时输出平滑的姿态角。

其他应用：

• 金融时间序列预测
• 机器人 SLAM（Simultaneous Localization and Mapping）
• 医疗信号处理（如 ECG 去噪）

---

4. 应用示例

示例：一维小车位置跟踪

假设小车匀速运动，用带噪声的 GPS 观测位置。

import numpy as np
import matplotlib.pyplot as plt

# 系统参数
dt = 1.0                          # 时间间隔
F = np.array([[1, dt], [0, 1]])   # 状态转移矩阵 (位置+速度)
H = np.array([[1, 0]])            # 观测矩阵 (只观测位置)
Q = np.diag([0.1, 0.01])          # 过程噪声协方差
R = np.array([[10]])               # 观测噪声协方差

# 初始化
x_est = np.array([0, 0])          # 初始状态 [位置, 速度]
P_est = np.eye(2)                 # 初始协方差矩阵

# 模拟数据
true_pos = np.array([t * 2 for t in range(1, 11)])  # 真实位置: 匀速运动
z_obs = true_pos + np.random.normal(0, np.sqrt(R[0,0]), 10)  # 带噪声观测

# 卡尔曼滤波
estimates = []
for z in z_obs:
    # 预测步骤
    x_pred = F @ x_est
    P_pred = F @ P_est @ F.T + Q
    
    # 更新步骤
    K = P_pred @ H.T @ np.linalg.inv(H @ P_pred @ H.T + R)
    x_est = x_pred + K @ (z - H @ x_pred)
    P_est = (np.eye(2) - K @ H) @ P_pred
    
    estimates.append(x_est[0])

# 可视化
plt.plot(true_pos, 'g-', label="True Position")
plt.plot(z_obs, 'ro', label="Noisy Observations")
plt.plot(estimates, 'b--', label="Kalman Estimates")
plt.legend()
plt.title("1D Kalman Filter Tracking")
plt.show()

输出效果：

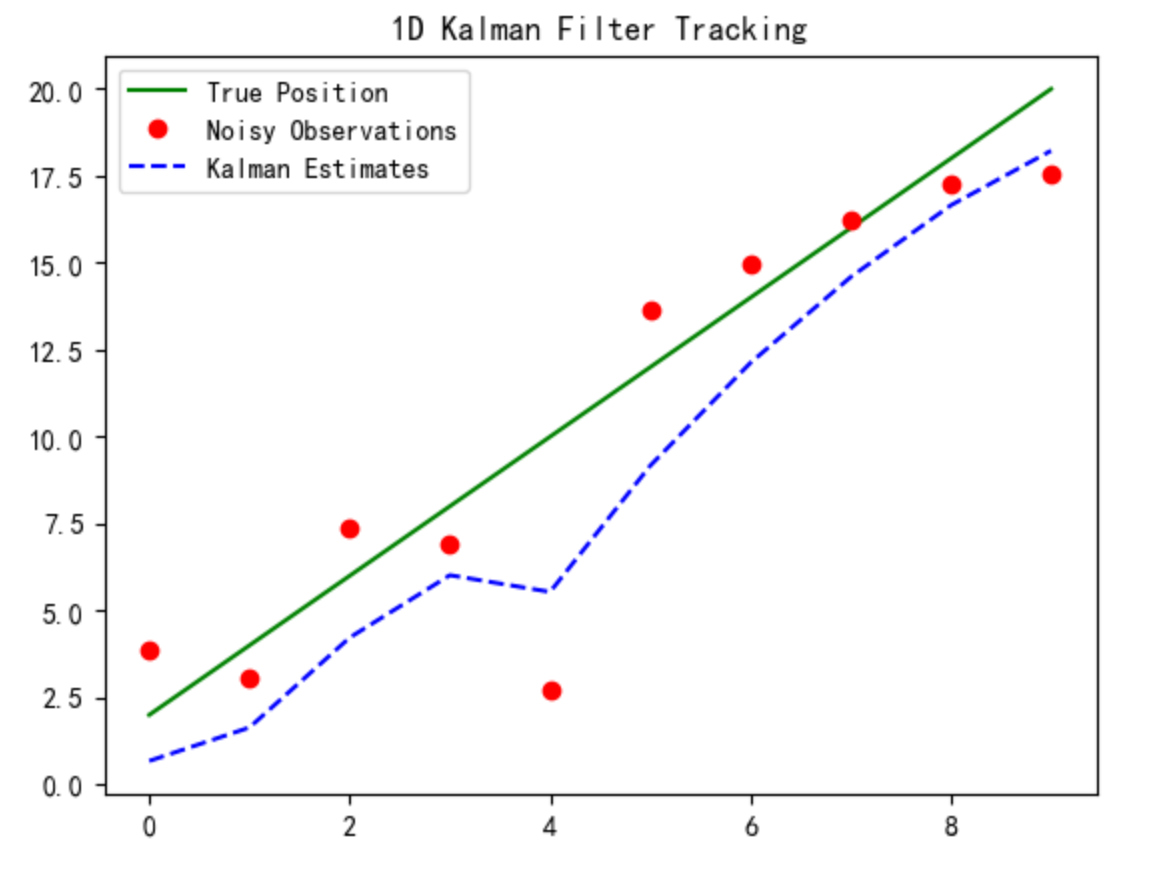
蓝色虚线（卡尔曼估计）比红色散点（观测值）更贴近绿色真实轨迹，有效过滤噪声。

---

5. 与其它技术对比

特性	卡尔曼滤波	移动平均（Moving Average）	粒子滤波（Particle Filter）
适用系统	线性高斯系统	静态序列	非线性/非高斯系统
计算复杂度	低 ($O(n^2)$)	极低 ($O(n)$)	高 ($O(N\cdot n)$)
实时性	优秀	优秀	较差
内存占用	低（仅存储矩阵）	低	高（存储粒子群）
多传感器融合支持	原生支持	不支持	支持

---

6. 类似技术

1. 扩展卡尔曼滤波（Extended Kalman Filter, EKF）
   • 通过泰勒展开线性化非线性系统，适用于弱非线性场景（如机器人运动学）。
2. 粒子滤波（Particle Filter）
   • 基于蒙特卡洛采样，适用于强非线性/非高斯系统（如目标跟踪中的遮挡处理）。

---

7. 总结

卡尔曼滤波是动态系统状态估计的基石算法，通过高效融合模型预测与噪声观测，在航空航天、自动驾驶等领域不可替代。其哲学启示：

---

官方资源：

• 原始论文
• MathWorks 卡尔曼滤波文档
• SciPy 状态空间模型

“在不确定的世界中，迭代优化是逼近真理的最佳路径。”——Kalman Filter 通过预测-更新循环动态融合系统模型与观测数据，在先验知识与实时测量间取得平衡。

---