剑指offer做题笔记Java版(1-40)

笔者记

笔者目前大四，虽然已经保研了，但研究生阶段是两年制专硕。找工作的压力也感到了些许，在学习科研的同时，也抽空准备工作方面的事情，如：算法基础、深度学习强化学习理论基础与面试常用题等。目前个人感觉科研方面出成果进大厂实验室较为困难，所以暂定目标为强化学习/深度学习的开发岗，与生产实践相结合，找工作的难度也相对容易。
本篇是剑指offer的刷题笔记上半部分，在此做一个记录，也供大家参考。笔记的下半部分可以点击链接：链接。

说明

题目旁边加*表示，该题较为有价值
题目旁边加#表示，该题有更好的解法，做完一遍之后必须回顾
题目旁边加&，表示该题还有知识点需要整理

20200120整理

剑指 Offer 03. 数组中重复的数字

该题第一个想法使用HashSet实现时空复杂度都为O(n)的查重算法，然后看了题解可以用置换的方法实现时间复杂度为O(n),空间复杂度为O(1)的算法。主要思路：因为n个数的范围0~n-1且其中有重复，我们将每个数字都放在对应的下标上必会出现重复。所以从下标为i从0开始，如果 (i!=nums[i]) 依次将nums[i] 置换到对应的位置上，直至找到两个位置上有重复为止。

剑指 Offer 04. 二维数组中的查找

该题二维数组中查找数字，如果和惯性思维从矩阵的左上角开始查找，则会陷入误区，难以快速找出答案。该题巧妙的解题思路在于从矩阵的右上角数字m开始，如果m大于要找的数target，则去除所在列；如果m小于target，则去除行；如果m等于target则返回结果。

剑指 Offer 05. 替换空格

原题是用c++去编写相关，所以设计字符操作，思路为：先计算移动后的字符串长度，再从后向前遍历，采用双指针分别指向当前字符串的末尾和移动后字符串的末尾，进行移动。在java中我使用String类的split方法解决了问题，在此需要注意的是，为了防止多个空格连续的情况，所以使用

String arr[] = s.split(" ",-1);

其中，-1表示尽可能多的使用正则表达式，可以保留连续的空格。思路为：先用split方法进行切割，然后用StringBuilder进行字符串连接。

剑指 Offer 06. 从尾到头打印链表

本题就是用栈去记录遍历过的结点，再依次出栈。虽然剑指offer上提及了方法递归的思路，但在leetcode上用java实现较为繁琐，就只用了栈+循环的方法，没有达到。

剑指 Offer 07. 重建二叉树（*）

本题结题思路为：前序遍历的第一点是根节点，并在中序遍历中找到该点，则中序遍历中该点前面的是左子树包含的，后面的是右子树包含的。由此再根据左右子树的前序和中序序列构建子树，递归求解。

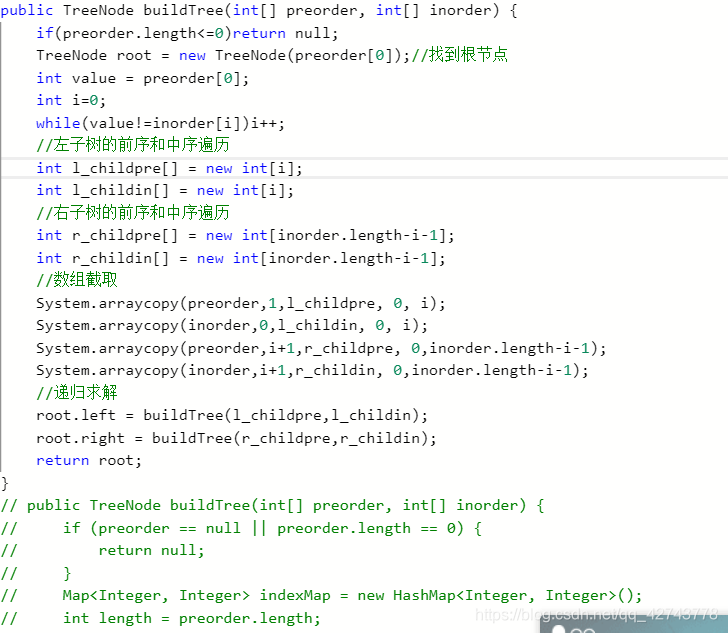
这是较为清晰的求解思路，但由于设计多次数组拷贝，开销较大，时间复杂度高。可以按照官方题解中的思路进行优化，即：在递归的过程中只传递左右子树相关的索引和整个数组，并使用一个Map存储中序遍历序列每个值所对应的下标，以方便查找。

剑指 Offer 09. 用两个栈实现队列（*）

主要思路为：栈1负责进队列，栈2负责出队列。入队列操作直接压入栈1，出队列操作如果栈2有则进行出栈，如果栈2为空则将栈1的元素压入栈2。如果栈1也为空，则返回1。

剑指 Offer 10. 斐波那契数列和青蛙跳台阶

解题思路：经典动态规划问题：f(n)=f(n-1)+f(n-2)

20200121整理

剑指 Offer 11.旋转数组的最小数字（双指针，二分查找）

采用双指针的形式进行解题，头指针 index1,尾指针 index2，中间指针indexMid。由于原来的数组是有序的，所以在旋转后可以分为三种情况讨论
1.numbers[indexMid]>numbers[index2]; 则去除左半部分，index1=indexMid+1
2.numbers[indexMid]<numbers[index2]; 则去除右半部分，index2=indexMid
3.numbers[indexMid]==numbers[index2]; 无法精准判断，index2–
最终index1指向最终的答案。注意：书中的解题思路与此类似，只是在等于的情况下采用遍历的形式进行解题。

剑指 Offer 12. 矩阵中的路径（回溯法）

回溯法的经典例题，exist方法体从矩阵的任意位置开始寻找字符串。search方法体从当前位置开始搜索所需字符串对应字符，满足以下所有条件才进行下一步搜索：
1.行列索引处于合法范围；
2.当前字符与字符串所需字符匹配；
3.当前字符未被访问过；
跳出递归的条件：如果当前搜索长度==字符串长度，则返回true。

剑指 Offer 13. 机器人的运动范围(回溯法）

这个也是用回溯法进行解题，check方法检验当前位置（row,col)是否可以被访问，moving方法计算当前位置及其后续位置共有多少个格子能够到达。用visited矩阵来记录当前位置是否被访问，以避免重复计算。

剑指 Offer 14- I. 剪绳子(动态规划）

经典的动态规划问题，一直知道动态规划是从上往下分析问题，从下往上解决问题。但在解决具体问题时，总是找不到递推关系。 解题思路：本题中，将多段剪绳子问题简化为剪一刀的问题。采用数组f[i]记录第i段绳子的最大乘积结果，然后进行递推。
在此需要注意的是：i=2时，乘积结果为1，但f[i]为2（因为在之后递推运算中可以不进行剪切，直接作为一整段绳子）。同样，i=3时，乘积结果为2，f[i]为3。当i>=4时，符合递推关系式，不用单独讨论。

剑指 Offer 14- II. 剪绳子 II(贪心算法+快速幂求余）

解题思路：当n的值过大时，最终结果会超出计算机可表示的数字范围，所以本题无法采用动态规划求解。可以采用贪心算法求解——当n>=5时，将绳子尽可能剪成长度为3的绳子，最终乘积最大。当n==4时，将绳子剪成长度为2的绳子，最终乘积最大。
并且在此还复习了一下如何实现快速幂算法。

剑指 Offer 15. 二进制中1的个数

解题思路：通过java中的位操作计算1的个数。
解法1：对n按位进行计算，先检测n的最后一位是不是1，然后将n进行无符号右移，每次移一位，再进行检测，直至n等于0.
解法2：将n与n-1进行与操作，这样就能将n最靠右边的1变为0，二进制其余位置上的数保持不变。比较巧妙的做法。

补充：java中位运算的相关知识

1.<< 左移，左边最高位丢弃，右边补齐0。
2.>> 右移，最高位是0，左边补齐0;最高为是1，左边补齐1。
3.>>> 无符号右移，无论最高位是0还是1，左边补齐0。
上述操作符加上=，则进行原变量上的赋值操作，如n>>>=1等价于n=n>>>1。
4.& 按位与操作，如：12&5，就是1100&101=0100，即等于4。
5.| 按位或操作，如：12|5，就是1100|0101=1101，即等于13。
6.^ 按位异或操作，如：12^5,就是1100 ^ 0101=1001，即等于9。
7.&& 短路与，两侧要求是布尔表达式。
8.|| 短路或，两侧要求是布尔表达式。

剑指 Offer 16. 数值的整数次方（快速幂）

本题解题思路：快速幂，使用快速幂解决问题。不过本题有多个需要注意的细节：
1.当指数为负值时，需要把底数x转换成1/x进行乘法运算。
2.n的范围是[-2^ 31,2^ 31-1]，所以当n=-2^ 31时，只能用long来表示底数的绝对值，才能乘以-1取对应绝对值。同时，因为2^ 31超出int范围，所以Math.abs失效了，并且当val为int时，乘以-1也失效了。

剑指 Offer 17. 打印从1到最大的n位数（分治/全排列）

这道题按照leetcode解题不难，但是面试的时候会考察大数的情况，需要用到分治和全排列的思想。下面先给出简单的解题方法，之后再详细记录一下大数情况下的解题过程。

如果n是1000甚至更大，那么则会超出int/long等常用数值的范围。那么本题需要采用字符串拼接来做，从高位到低位以此确定，并且需要注意：1、高位多余的0需要去除。2、记录从1开始打印。

剑指 Offer 18. 删除链表的节点

链表中删除结点的技巧：将后续结点的值和后续结点的next结点覆盖到所要删除节点的原有内容，等价于删除该节点。

20200126整理

剑指 Offer 19. 正则表达式匹配(#)

解题思路：按照原书上的思路，通过有限状态机分析进行递归解题。如果匹配串下一位无 *，则按位比较；如果匹配串有 *，则分三种情况：
1.原字符串后移一位，匹配串保持不变；
2.原字符串后移一位，匹配串也往后移两位；
3.原字符串保持不变，匹配串后移两位，表示当前匹配串字符出现0次。

剑指 Offer 20. 表示数值的字符串(注意细节)

本题思路不难，就是需要注意细节，各种恶心的测试用例都有涉及。需要注意如下几点：
1.±号只能出现在数字最开始或者e/E后面，不能出现在数字之间。
2.空格只能出现在字符串的开头和结尾，中间的空格是不允许的。
3.’.‘只能出现在e/E之前，不能出现在其后面。
4.e/E出现在数字后面，且不能出现在结尾。
5.最后一个非空格字符只能是数字或者’.’。
6.整个字符串必须包含数字。

本题我被坑的测试用例在此做个总结，以免后人多次提交：
“e9”、“1 “、” “、”.1”、“3.”、"."、". 1"、“1 4”、" 0"、“1 .”、“0e “、“6+1”、”.-4”、"+ 1"

如果想直接拷贝代码，可以访问这个详细版：链接

剑指 Offer 21. 调整数组顺序使奇数位于偶数前面(双指针/快慢指针)

解题思路：
1.双指针：采用头指针和尾指针，头指针找到偶数，尾指针找到奇数，然后互换位置，直至头指针索引大于等于尾指针。
2.快慢指针：采用两个指针从头开始，慢指针寻找偶数，快指针寻找奇数进行位置互换，每次置换完成后，慢指针++，直至快指针到达数组结尾。

剑指 Offer 22. 链表中倒数第k个节点(双指针)

解题思路：
最初的思路：采用栈，遍历一遍，然后弹出到第k个节点。
进阶版思路：采用双指针，第一个指针先走k-1步，第二个指针再出发，则当第一指针到末尾时，第二个指针正好指向倒数第k个节点。

剑指 Offer 24. 反转链表

解题思路：
迭代版：对于每个节点，都需要记录它的前置节点，以进行反转。并且在反转前需要记录其后继节点，避免链表断开。直至当前节点为null，则表示链表反转完成。
递归版：1.需要返回原链表的最后一个节点，2.在原链表的基础上对于每个节点进行反转（将当前节点后继节点的后继节点设置为当前节点），并且在反转完成后避免成环，需要将当前节点后继节点置空。

剑指 Offer 25. 合并两个排序的链表

解题思路：因为合并列表开始是空的，所以采用伪头节点的方式进行合并。如果l1和l2都不为空，就选中其中较小的节点添加到合并列表中，直至l1为空或者l2为空。然后将剩余数组链接在合并数组的最后。

剑指 Offer 26. 树的子结构（先序遍历+包含判断）

解题思路：
1.判断以当前节点为根是否包含子结构；判断左子树是否包含子结构；判断右子树是否包含子结构。
2.判断以当前节点为根是否包含子结构的条件为：是否当前节点值相等，并且左孩子、右孩子的相应节点也相等。
该题解题的关键是根节点的确定，以及子结构包含条件的判断。

剑指 Offer 27. 二叉树的镜像

解题思路：将根节点的左右子树进行互换，并且对左右孩子节点以此递归进行镜像操作。

剑指 Offer 28. 对称的二叉树

解题思路：从根节点的左右节点出发，如果对称，则左节点的右孩子等于右节点的左孩子，并且左节点的左孩子等于右节点的右孩子。并且在向下递归的时候，符合上述规律。因此进行递归判断。本题解题思路中引入输入参数为两个节点的辅助函数是十分精妙的，大大简化了解题步骤。

剑指 Offer 29. 顺时针打印矩阵

解题思路：通过模拟进行解题，依次向左、向下、向右、向上进行打印，边界条件较为复杂，解题时需要细心分析。

20200201整理

剑指 Offer 30. 包含min函数的栈（辅助栈）

解题思路：采用辅助栈记录最小值。入栈条件：x<=min.peek()，其中的等号保证了有多个相等最小值时，不会因为多次弹出而导致空栈的情况。

剑指 Offer 31. 栈的压入、弹出序列（辅助栈）

解题思路：采用辅助栈模拟两个序列的压入和弹出操作。从弹出序列依次比对，如果该元素未在栈中，则将该元素及其前面元素进行入栈操作；如果该元素在栈中，则进行弹出，然后判断弹出序列的下一个元素。

剑指 Offer 32 - I. 从上到下打印二叉树

解题思路：采用队列进行层序遍历

剑指 Offer 32 - II. 从上到下打印二叉树 II

解题思路：本题与Ⅰ不同之处在于，需要确定每层节点的个数。解析代码中在每层的开始通过：i = queuq.size()获取当前层的节点个数，虽然queue中的节点数是不断变化的，但是for循环中的代码只在开始进行获取并赋值给i，然后对i进行操作，所以不会被影响。在看完官方给的解析后，我觉得这一步非常精妙，避免了额外设置变量等冗余操作。

剑指 Offer 32 - III. 从上到下打印二叉树 III

解题思路：该题与Ⅱ的不同之处在于偶数行的结果需要反向打印，所以在偶数行添加时采用LinkedList带有的addFirst()函数，在列表开头插入元素。最终显示效果为偶数行从右到左进行打印。

剑指 Offer 33. 二叉搜索树的后序遍历序列（#）

解题思路：后序遍历序列的最后一个节点是根节点，根据二叉搜索树的性质，前面节点的值可以分为两部分：小于根节点的值属于其左子树，大于根节点的值属于其右子树，然后再递归判断左右子树。

剑指 Offer 34. 二叉树中和为某一值的路径（递归回溯）

解题思路：递归回溯进行解题，dfs过程中传递的值是已经经过的结点、当前节点、剩余的sum值。如果当前节点为叶子节点，且sum恰好为0，则找到一条路径；如果不为叶子节点，则继续往左右子树中进行搜索。并且在开始时将当前节点加入路径path，在回溯时，将当前节点移出路径path。

剑指 Offer 35. 复杂链表的复制（#）

解题思路：本题对复杂链表进行复制时，难点为：节点random指针复制时不便查找。在进行链表基本元素复制时，将原节点N和复制节点N’加入到HashMap中，从而在random指针复制时，可以在O(1)复杂度下找到节点。
进阶思路：采用链表拼接和拆分方式进行复制。1.将复制节点直接连接在原节点的后面。2.复制节点random所指向的节点正好是原节点所指向节点的下一个节点。3.将链表按照奇偶进行拆分，拆成两个链表。

剑指 Offer 36. 二叉搜索树与双向链表（*）

解题思路：本题想到了用中序遍历来解，但是在中序时对于指针的具体操作一直没有想明白，最终看了题解，恍然大悟。首先将前一节点pre和头节点head设为全局变量，采用前一节点pre的好处如下：
1.当pre为空时，意味着还未找到头节点head。
2.采用前一节点，只需更改当前节点node的left指针，不会影响原有中序遍历后半部分的运行。
3.当没有后继节点时，pre记录的正好是循环链表的尾节点。

具体代码如下，简洁明了，思路清晰。

剑指 Offer 37. 序列化二叉树(前序遍历+反序列）

解题思路：将原有二叉树进行前序遍历，并对于空节点采用“$“进行记录，节点间采用”,"进行分割。然后再根据前序遍历序列进行反序列解码。

剑指 Offer 38. 字符串的排列（全排列+回溯法*）

解题思路：第一步，固定第一个元素。第二步，递归求剩余字符的全排列。以此来减少问题规模。在固定完第一个元素后，需要将其和后面字符进行换位，以获得全排列的情况。

比如：以"abcd"为例，
第一步固定第一个元素，依次递归，得到”abcd"。
然后c和d进行置换，得到“abdc"。
回溯到b，b和c进行置换，并进行递归固定得到”acbd“,
然后b和d进行置换，得到"acdb"。
再次回溯到b,b和d进行置换，递归固定得到“adcb",
然后c和b进行置换，得到”adbc"。
至此，以a开头的字符串已经全部得到，然后开始置换，分别以b、c、d开头。

剑指 Offer 39. 数组中出现次数超过一半的数字

简单题没啥好说的。摩尔投票法挺精妙的，通过众数的性质进行快速解题。

剑指 Offer 40. 最小的k个数

解题思路:直接排序，找到最小的k个数，时间复杂度O(nlogn)。
可以用大顶堆存最小的k个数，以此来优化，时间复杂度O(nlogk)。但实际操作时，由于堆的插入和删除消耗时间较多，并未提升最终的性能。