主成分分析（PCA）原理总结

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

主成分分析（Principal components analysis，以下简称PCA）是最常用的降维方法之一，在数据压缩和消除冗余方面具有广泛的应用，本文由浅入深的对其降维原理进行了详细总结。

目录

---

1.向量投影和矩阵投影的含义

2. 向量降维和矩阵降维的含义

3. 基向量选择算法

4. 基向量个数的确定

5. 中心化的作用

6. PCA算法流程

7. PCA算法总结

1. 向量投影和矩阵投影的含义

如下图：

向量a在向量b的投影为：

其中，θ是向量间的夹角 。

向量a在向量b的投影表示向量a在向量b方向的信息，若θ=90°时，向量a与向量b正交，向量a无向量b信息，即向量间无冗余信息 。因此，向量最简单的表示方法是用基向量表示，如下图：

向量表示方法：

其中，c1是在e1方向的投影，c2是在e2方向的投影，e1和e2是基向量

我们用向量的表示方法扩展到矩阵，若矩阵的秩r(A)=n，

，其中ai（i=1,2,...,n）为n个维度的列向量，那么矩阵A的列向量表示为：

其中，e1，e2，...，en为矩阵A的特征向量 。

若矩阵A是对称矩阵，那么特征向量为正交向量，我们对上式结合成矩阵的形式：

由上式可知，对称矩阵A在各特征向量的投影等于矩阵列向量展开后的系数，特征向量可理解为基向量。

2. 向量降维和矩阵降维含义

向量降维可以通过投影的方式实现，N维向量映射为M维向量转换为N维向量在M个基向量的投影，如N维向量，M个基向量分别为，在基向量的投影：

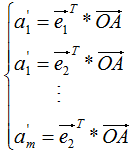
通过上式完成了降维，降维后的坐标为：

矩阵是由多个列向量组成的，因此矩阵降维思想与向量降维思想一样，只要求得矩阵在各基向量的投影即可，基向量可以理解为新的坐标系，投影就是降维后的坐标，那么问题来了，如何选择基向量？

3. 基向量选择算法

已知样本集的分布，如下图：

样本集共有两个特征x1和x2，现在对该样本数据从二维降到一维，图中列了两个基向量u1和u2，样本集在两个向量的投影表示了不同的降维方法，哪种方法好，需要有评判标准：（1）降维前后样本点的总距离足够近，即最小投影距离；（2）降维后的样本点（投影）尽可能的散开，即最大投影方差 。因此，根据上面两个评判标准可知选择基向量u1较好。

我们知道了基向量的选择标准，下面介绍基于这两个评判标准来推导基向量：

（1）基于最小投影距离

假设有n个n维数据，记为X。现在对该数据从n维降到m维，关键是找到m个基向量，假设基向量为{w1,w2,...,wm}，记为矩阵W，矩阵W的大小是n×m。

原始数据在基向量的投影：

投影坐标计算公式：

根据投影坐标和基向量，得到该样本的映射点：

最小化样本和映射点的总距离：

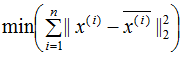
推导上式，得到最小值对应的基向量矩阵W，推导过程如下：

所以我们选择的特征向量作为投影的基向量 。

(2) 基于最大投影方差

我们希望降维后的样本点尽可能分散，方差可以表示这种分散程度。

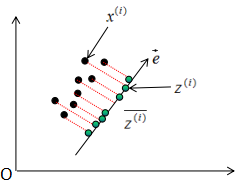
如上图所示，表示原始数据，表示投影数据，表示投影数据的平均值。所以最大化投影方差表示为：

下面推导上式，得到相应的基向量矩阵W，推导过程如下：

我们发现(4)式与上一节的(13)式是相同的。

因此，基向量矩阵W满足下式：

小结：降维通过样本数据投影到基向量实现的，基向量的个数等于降维的个数，基向量是通过上式求解的。

4. 基向量个数的确定

我们知道怎么求解基向量，但是我们事先确定了基向量的个数，如上节的m个基向量，那么怎么根据样本数据自动的选择基向量的个数了？在回答这一问题前，简单阐述下特征向量和特征值的意义。

假设向量wi，λi分别为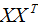的特征向量和特征值，表达式如下：

对应的图：

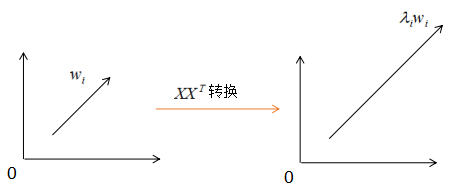
由上图可知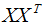，没有改变特征向量wi的方向，只在wi的方向上伸缩或压缩了λi倍。特征值代表了在该特征向量的信息分量。特征值越大，包含矩阵的信息分量亦越大。因此，我们可以用λi去选择基向量个数。我们设定一个阈值threshold，该阈值表示降维后的数据保留原始数据的信息量，假设降维后的特征个数为m，降维前的特征个数为n，m应满足下面条件：

因此，通过上式可以求得基向量的个数m，即取前m个最大特征值对应的基向量 。

投影的基向量：

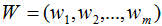
投影的数据集：

5. 中心化的作用

我们在计算协方差矩阵的特征向量前，需要对样本数据进行中心化，中心化的算法如下：

中心化数据各特征的平均值为0，计算过程如下：

对上式求平均：

中心化的目的是简化算法，我们重新回顾下协方差矩阵，以说明中心化的作用 。

，X表示共有n个样本数。

每个样本包含n个特征，即：

展开: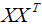

为了阅读方便，我们只考虑两个特征的协方差矩阵：

由(3)式推导(2)式得：

所以是样本数据的协方差矩阵，但是，切记必须事先对数据进行中心化处理 。

6. PCA算法流程

1）样本数据中心化。

2）计算样本的协方差矩阵。

3）求协方差矩阵的特征值和特征向量，并对该向量进行标准化（基向量）。

3）根据设定的阈值，求满足以下条件的降维数m。

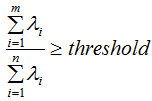
4）取前m个最大特征值对应的向量，记为W。

5）对样本集的每一个样本，映射为新的样本。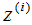

6）得到映射后的样本集D'。

7.核主成分分析（KPCA）介绍 

因为可以用样本数据内积表示：

由核函数定义可知，可通过核函数将数据映射成高维数据，并对该高维数据进行降维：

KPCA一般用在数据不是线性的，无法直接进行PCA降维，需要通过核函数映射成高维数据，再进行PCA降维 。

8.PCA算法总结

PCA是一种非监督学习的降维算法，只需要计算样本数据的协方差矩阵就能实现降维的目的，其算法较易实现，但是降维后特征的可解释性较弱，且通过降维后信息会丢失一些，可能对后续的处理有重要影响。

参考

https://www.cnblogs.com/pinard/p/6239403.html#undefined

A Singularly Valuable Decompostion: The SVD of a Matrix

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲

在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~