动态规划dp

01背包详解

题目背景

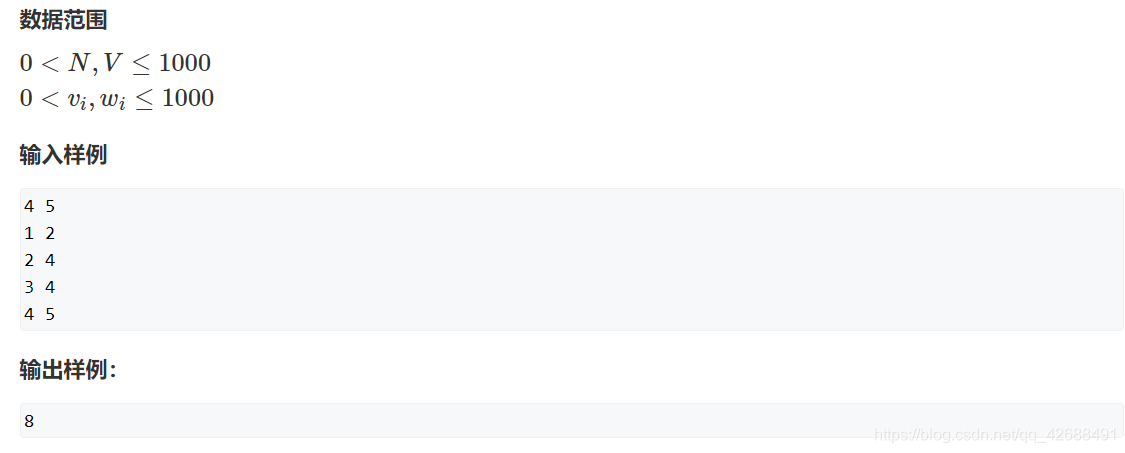
题解

01背包的特点是
一个物品只能选一次
而且本题求最大收益（价值）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MAX = 1e9;
const int MIN = -1e9;
const int N = 1e6 + 10;
int n , v;
struct Node{
    int val;
    int space;
}P[N];
int dp[10000][10000];

int main(){
    cin >> n >> v;
    for(int i = 1; i <= n ; i++) cin >> P[i].space >> P[i].val;
    for(int i = 1 ; i <= n ; i++)
    {
        for(int j = 0 ; j <= v ; j++)
        {
            //状态转移方程
            if( P[i].space > j ) dp[i][j] = dp[i-1][j];
            else dp[i][j] = max( dp[i-1][j] , dp[i-1][j-P[i].space] + P[i].val );
        }
    }
    cout << dp[n][v] << endl;




    return 0;
}

状态转移方程：

当前状态的值取决于前一个状态的值的最优解，所以我们第一重循环，是按照物品一次向后

状态dp[ i ] [ j ]表示，前 i 个物品，在背包容量为 j 的情况下最大价值

当背包容量不够时，无法选择物品，即：

if( P[i].space > j ) dp[i][j] = dp[i-1][j];

当背包容量够的时候，我们考虑选或者不选的问题

dp[i][j] = max( dp[ i - 1 ][ j ] , dp[ i - 1 ][ j - P[i].space ] + P[i].val )

继而得到状态转移方程