专为新手入门二叉树（C实现）

本篇博客主要涉及二叉树的基本操作，创建，三种遍历，求节点等（C写法）。

二叉树作为数据结构的难点，想必让很多人望而生畏，各种复杂的代码和算法实在让人头大，博主也是近期刚接触二叉树，对于二叉树的探究也不是很深刻，所以有纰漏还请体谅。

1.首先了解下二叉树
二叉树其实是树的一种特殊形式，数据结构中除了图也就是树最难了，二叉树的定义是采用的一种递归方式（如果不了解递归，可自行百度或者看看其他大牛关于递归的详细阐述，新手可能在刚接触递归的时候老是担心递归的细节会不会出错，其实递归的中心思想就是把大问题切割成小问题而已）。

二叉树的特点有：点的度只可能为0,1,2，度为2的点个数+1=叶子结点个数等。
2.下面直接进入二叉树的实现
二叉树的数据结构也包含顺序和链序的，其实就是分别通过数组和指针来实现，考虑到二叉树的结构，选择链序的会更好。

所以可以写出二叉树数据结构

struct btnode{
		char data;
		btnode* lchild;
		btnode* rchild;
};  
3.二叉树的创建
知道了二叉树的存储结构，怎么去建立一棵二叉树呢，递归方法是最为便捷和最好理解的。
	

void create(btnode* &T)
    {
    	char c;
    	scanf("%c",&c);
    	if(c=='/')                /*     若输入为'/',则认为该结点为空  */
    			return;
    	T=new btnode;
    	T->data=c;
    	T->lchild=NULL;
    	T->rchild=NULL;
    	create(T->lchild);
    	create(T->rchild);
    }

4.二叉树的三种遍历
二叉树的遍历包括先序、中序、后序（三种方法本质一样，在这只详细介绍先序遍历）
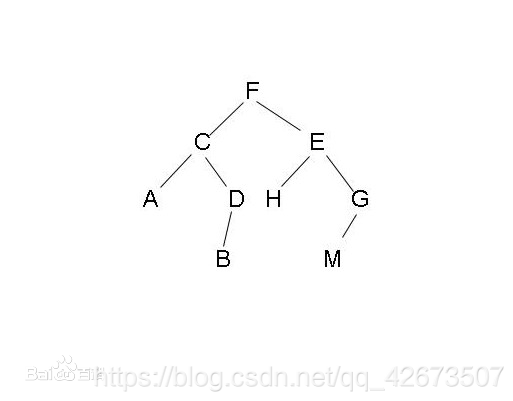
先序遍历的规则是先visit根节点，再vistit该根节点的左孩子，再vistit该根节点的右孩子，如下图二叉树的先序遍历输出为：
F>C>A>D>B>E>H>G>M
思想就是

代码实现为

void prior_order1(btnode* T)     //递归先序遍历二叉树
{
	if(T)     //节点为空直接跳出
	{
		cout<<T->data;
		prior_order1(T->lchild);
		prior_order1(T->rchild);
	}
}

中序和后序只需要把（cout<data;）换下顺序就可以了，我相信大家还是很好理解的。
5.二叉树的层数
求二叉树的层数其实也是采用递归方法

int depth(btnode* T)//求二叉树的深度,规定根节点所在层次为0层 
{
	int leftlen,rightlen;
	if(T==NULL)
		return 0;
	else
	{
		 leftlen=depth(T->lchild)+1;
		 rightlen=depth(T->rchild)+1;
	}
	if(leftlen>rightlen)
		return leftlen;
	return rightlen;                 //就是比较左右子树的深度，选择较大的，
}

6.求叶子结点个数

void leaf(btnode* T,int &count)//求叶子节点个数
{
	if(T)
	{	
	
		if(T->lchild==NULL &&T->rchild== NULL)
			count=count+1;
		leaf(T->lchild,count);
		leaf(T->rchild,count);	
	}
} 

其实掌握了这些方法，二叉树的其他操作的思想也是差不多的。
最后附上全部代码

#include<stdio.h>
#include<iostream>
using namespace std;

struct btnode{
	char data;
	struct btnode *lchild,*rchild;
};
extern int level=0;
extern	int count=0;
int depth(btnode* );
void create(btnode* &T)
{
	char c;
	scanf("%c",&c);
	if(c=='/')      //若为'/',则该结点为空
		return;
	T=new btnode;
	T->data=c;
	T->lchild=NULL;
	T->rchild=NULL;
	create(T->lchild);
	create(T->rchild);
}
void prior_order1(btnode* T)//递归先序遍历二叉树
{
	
	if(T)
	{
		cout<<T->data<<;
		prior_order1(T->lchild);
		prior_order1(T->rchild);
	}
}
void mid_order(btnode* T)//递归中序遍历二叉树
{
	if(T)
	{
		mid_order(T->lchild);
		cout<<T->data<<;
		mid_order(T->rchild);
	}
}
void behind_bt(btnode*T)//后续遍历二叉树
{
	if(T)
	{
		behind_bt(T->lchild);
		behind_bt(T->rchild);
		cout<<T->data<<;
	}

}
void prior_order(btnode* T)//先序输出二叉树 ，并且同时输出每个节点对应的位数 
{
	int count=1;
	if(T==NULL)
		 return;
	printf("(%c,%d) ",T->data,count++);
	if(T->lchild)
		printf("(%c,%d) ",T->lchild->data,count);
	if(T->rchild)
		printf("(%c,%d) ",T->rchild->data,count);
}
void numbers_of_node(btnode* T,int &count)//计算二叉树中结点个数，赋值给count 
{
	if(T)
	{
		++count;
		numbers_of_node(T->lchild,count);
		numbers_of_node(T->rchild,count);
	}
}
int depth(btnode* T)//求二叉树的深度,规定根节点所在层次为0层 
{
	int leftlen,rightlen;
	if(T==NULL)
		return 0;
	else
	{
		 leftlen=depth(T->lchild)+1;
		 rightlen=depth(T->rchild)+1;
	}
	if(leftlen>rightlen)
		return leftlen;
	return rightlen;
}
void leaf(btnode* T,int &count)//求叶子节点个数
{
	if(T)
	{	
		if(T->lchild==NULL&&T->rchild==NULL)
			count=count+1;
		leaf(T->lchild,count);
		leaf(T->rchild,count);	
	}
} 
int main()
{
	btnode *T=new btnode;
	T=NULL;
	int num1,node;
	num1=node=0;
	create(T);
	leaf(T,num1);//num1保存叶子结点个数 
	numbers_of_node(T,node);//node保存结点个数 
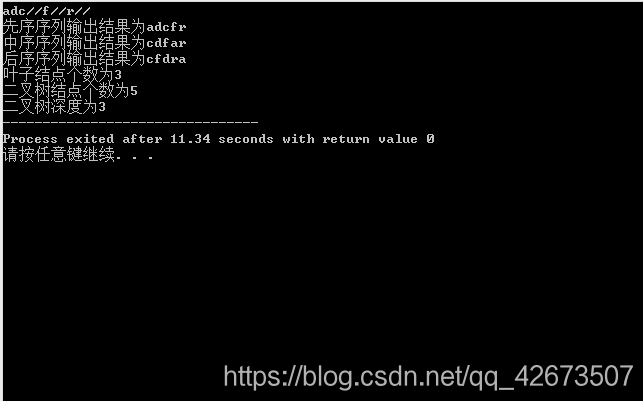
	cout<<"先序序列输出结果为";
	prior_order1(T);	cout<<'\n'; 
	cout<<"中序序列输出结果为";
	mid_order(T);	    cout<<'\n'; 
	cout<<"后序序列输出结果为";
	behind_bt(T);	    cout<<'\n';
	cout<<"叶子结点个数为"<<num1<<endl;
	cout<<"二叉树结点个数为"<< node<<endl;
	cout<<"二叉树深度为"<<depth(T);
	return 0;
}

相信只要努力了肯定就有所收获的，大家看不懂代码的时候就照着打几遍，不懂也能记下来了，久而久之慢慢就掌握了。