数据结构——树—— 二叉树及存储结构

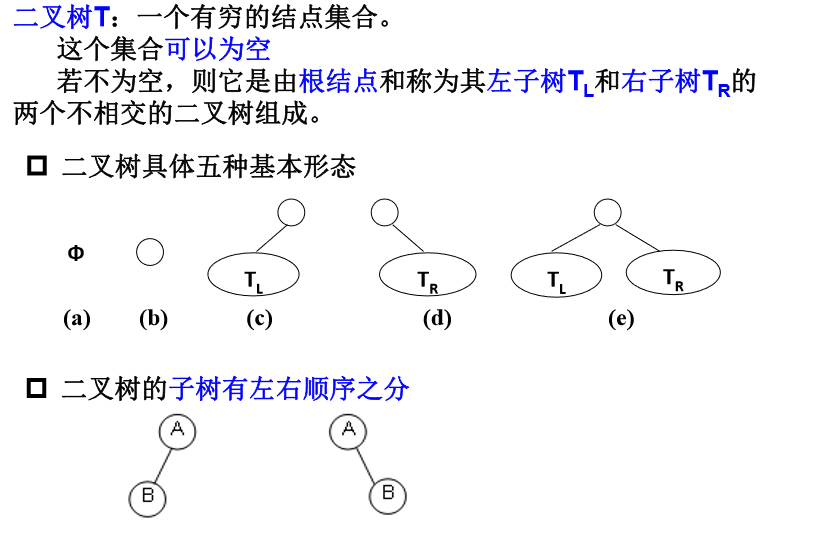
在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。
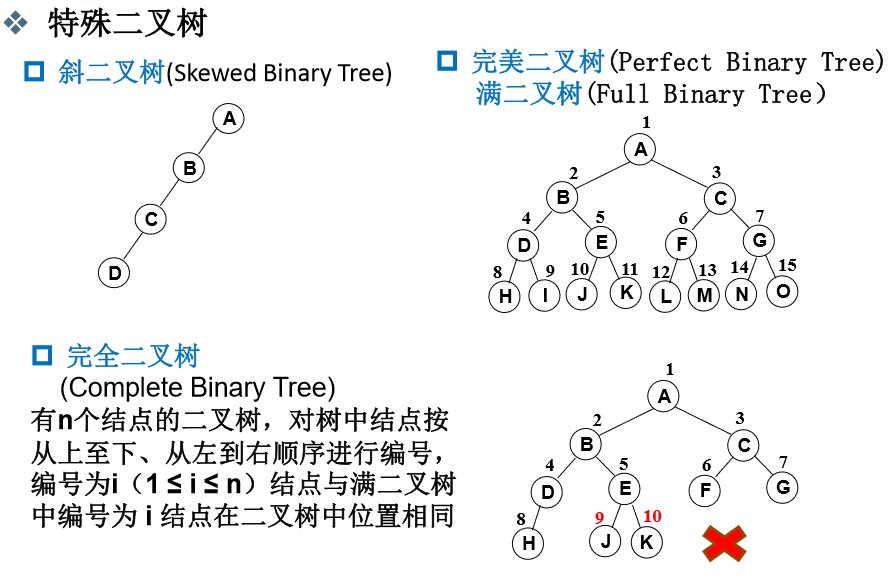
一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。这种树的特点是每一层上的节点数都是最大节点数。而在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在右边缺少连续若干节点，则此二叉树为完全二叉树。具有n个节点的完全二叉树的深度为floor(log2n)+1。深度为k的完全二叉树，至少有 2^k-1个叶子节点，至多有 2^k-1个节点。

二叉树重要性质

(1) 在非空二叉树中，第i层的结点总数不超过2^(i-1), i>=1；
(2) 深度为h的二叉树最多有2^h -1个结点(h>=1)，最少有h个结点；
(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；
(4) 具有n个结点的完全二叉树的深度为[log2^n]+1
（注：[ ]表示向下取整）
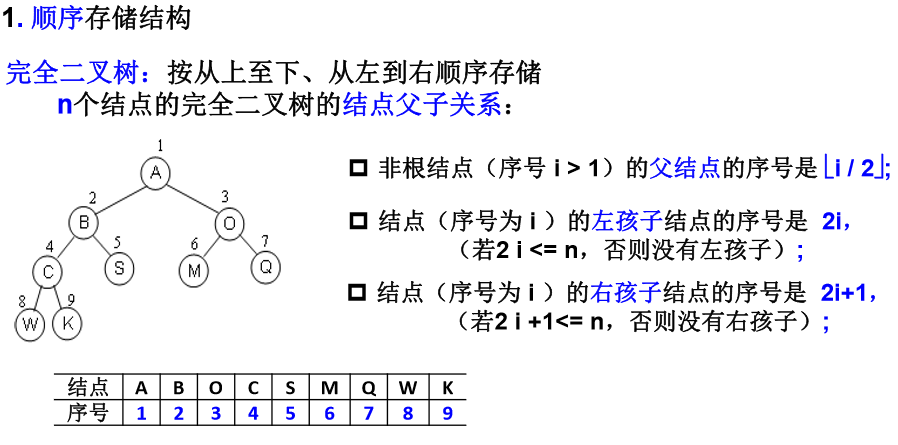
(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
若I为结点编号则 如果I>1，则其父结点的编号为I/2；
如果2I<=N，则其左孩子（即左子树的根结点）的编号为2I；若2I>N，则无左孩子；
如果2I+1<=N，则其右孩子的结点编号为2I+1；若2I+1>N，则无右孩子。
(6)给定N个节点，能构成h(N)种不同的二叉树。
h(N)为卡特兰数的第N项。h(n)=C(2*n，n)/(n+1)。
(7)设有i个枝点，I为所有枝点的道路长度总和，J为叶的道路长度总和J=I+2i

二叉树的抽象数据类型定义
类型名称：二叉树 数据对象集：一个有穷的结点集合。 若不为空，则由根结点和其左、右二叉子树组成。
重要操作有： 1、Boolean IsEmpty( BinTree BT )： 判别BT是否为空； 2、void Traversal( BinTree BT )：遍历，按某顺序访问每个结点； 3、BinTree CreatBinTree( )：创建一个二叉树。

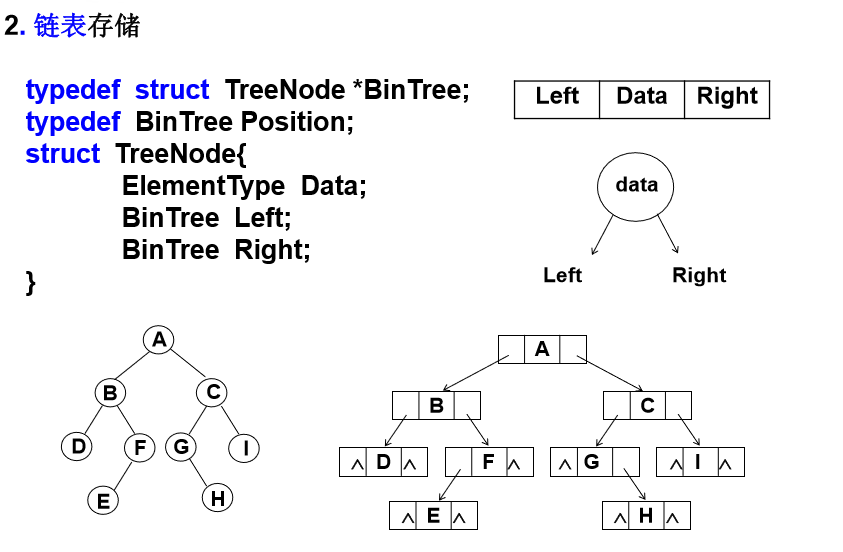
    typedef struct TNode *Position;
    typedef Position BinTree; /* 二叉树类型 */
    struct TNode{ /* 树结点定义 */
        ElementType Data; /* 结点数据 */
        BinTree Left;     /* 指向左子树 */
        BinTree Right;    /* 指向右子树 */
    };

二叉树的存储结构