SIFT算子实现特征匹配

SIFT算子原理

首先我们要知道SIFT实现特征匹配的大致流程：

1. 提取关键点
2. 对关键点附加详细的信息(此部分具有的特征)，即描述符。
3. 通过特征点两两比较找出相互匹配的若干对特征点，建立景物间的对应关系。

如何提取关键点

1. 何为关键点？
   这些点是一些十分突出的点不会因光照、尺度、旋转等因素的改变而消失，比如角点、边缘点、暗区域的亮点以及亮区域的暗点。即这些特征点要能够具有尺度、方向、位移、光照不变性。
2. 关键点检测
   如何做到满足尺度不变性呢？若我们对原始图像进行尺度变换，获得图像多尺度下的空间表示。从而实现边缘、角点检测和不同分辨率上的特征提取，以满足关键点的尺度不变性。尺度空间中的各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。要记住：尺度越大图像越模糊！
   如何对图像进行模糊处理呢？高斯核是唯一可产生多尺度空间的核。可以用原始图像与二维高斯函数进行卷积运算。

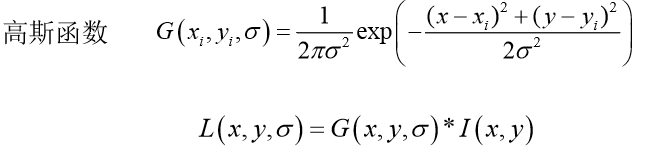
在具体实现尺度空间时需要构建高斯金字塔，而构建过程分为两步骤：1.对图像做不同尺度的高斯模糊，2.对图像做降采样(隔点采样)。

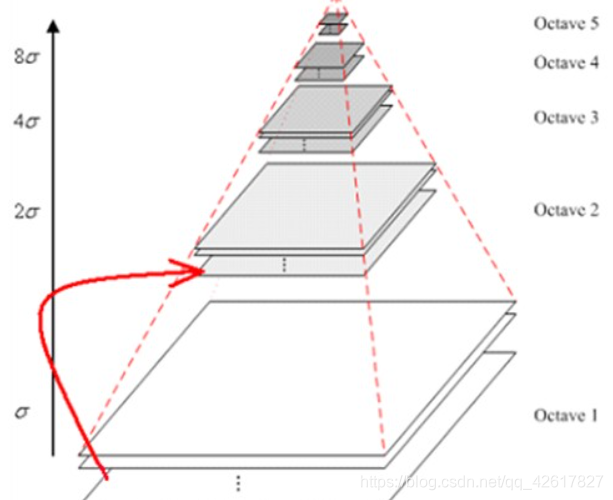
图像的金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像)，每个金字塔共n层。
为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如上图，将图像金字塔每层的一张图像使用不同参数做高斯模糊，使得金字塔的每层含有多张高斯模糊图像，将金字塔每层多张图像合称为一组(Octave)，金字塔每层只有一组图像，组数和金字塔层数相等，每组含有多张(也叫层Interval)图像。另外，降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。
高斯图像金字塔共o组，s层，则有:

最后可将组内和组间尺度尺度归为

接下来使用高斯差分函数DOG产生比较稳定的图像特征。函数为：

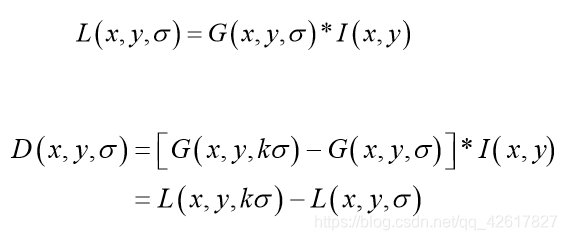
在实际计算时，使用高斯金字塔每组中相邻上下两层图像相减，得到高斯差分图像，进行极值检测，如图:

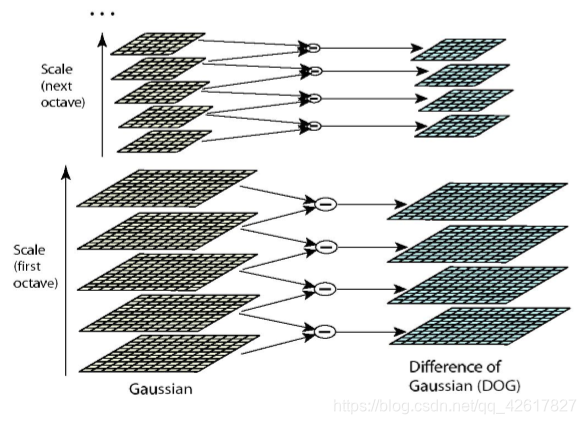
如果相减之后的结果没有变化，也就是没有特征。而特征必须是变化尽可能多的点。DOG图像描绘的是目标的轮廓。
寻找DOG的局部极值点。因为关键点是由DOG的局部极值点构成的。为了寻找DoG函数的极值点， 每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域 的相邻点大或者小。

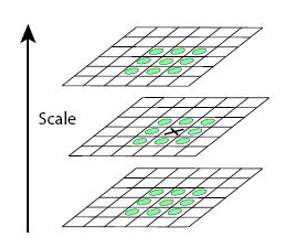
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个 点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。又由于DOG函数在图像边缘有较强的边缘响应，因此需要排除不稳定的边缘响应点。获取特征点处的Hessian矩阵，主曲率通过一个2x2 的Hessian矩阵H求出：