第五章-Logistic回归
分类
在分类问题中,你要预测的变量 y y y 是离散的值,我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。我们从二元的分类问题开始讨论,分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否存在欺诈;判断一个肿瘤是恶性的还是良性的。
我们将因变量(dependent variable)可能属于的两个类分别称为负类(negative class) 和 正类(positive class),则因变量 y ∈ 0 , 1 y\in { 0,1 } y∈0,1 ,其中 0 表示负类,1 表示正类。
负向类和正向类的选取没有明确的规定,谁是负类,谁是正类完全取决于你自己的意愿,但是通常情况下我们把负类表示为没有某样东西,把正类表示为具有我们要寻找的东西。比如肿瘤预测,没有恶性肿瘤的选取为负类,有恶性肿瘤的选取为正类。
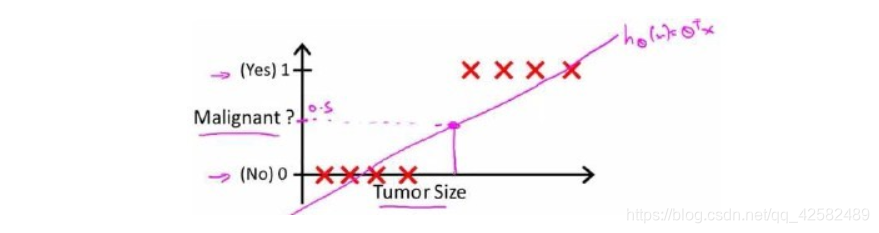
对于肿瘤预测的分类问题,我们可以用线性回归的方法求出适合数据的一条直线。根据线性回归模型我们只能预测连续的值,然而对于分类问题,我们需要输出0或1,因此我们可以预测:
当 h θ ( x ) > = 0.5 {h_\theta}\left( x \right)>=0.5 hθ(x)>=0.5时,预测 y = 1 y=1 y=1。
当 h θ ( x ) < 0.5 {h_\theta}\left( x \right)<0.5 hθ(x)<0.5时,预测 y = 0 y=0 y=0 。
对于上图的数据而言,这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤,将其作为实例加入到我们的训练集中来,这将使得我们获得一条新的直线。
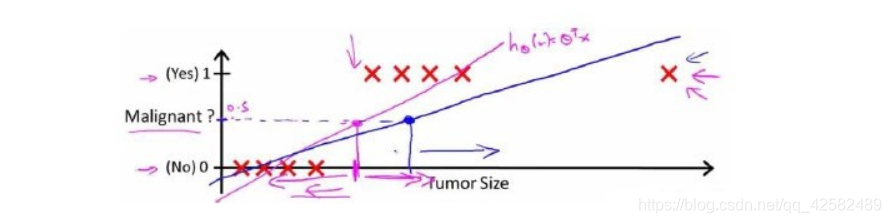
这时,再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。
可以看出,线性回归模型,因为其预测的值可以超越[0,1]的范围,并不适合解决这样的问题。使用线性回归的方法来拟合数据的结果显然不是一个好的方法,不建议将线性回归用于分类问题。
如果我们要用线性回归算法来解决一个分类问题,对于分类, y y y 取值为 0 或者1,如果你使用的是线性回归,那么假设函数的输出值可能远大于 1,或者远小于0,即使所有训练样本的标签 y y y 都等于 0 或 1,这样的结果会让人觉得很奇怪。于是我们考虑使用逻辑回归算法,这个算法的性质是:它的输出值永远在0到 1 之间。
逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法,它适用于标签 y y y 取值离散的情况,如:0 1 2 3。
假设陈述
我们引入一个新的模型,逻辑回归模型,该模型的输出变量范围始终在0和1之间。
逻辑回归模型的假设是: h θ ( x ) = g ( θ T X ) h_\theta \left( x \right)=g\left(\theta^{T}X \right) hθ(x)=g(θTX)
其中: X X X 代表特征向量, g g g 代表 逻辑函数(logistic function) 是一个常用的逻辑函数为S形函数(Sigmoid function),公式为: g ( z ) = 1 1 + e − z g\left( z \right)=\frac{1}{1+{
{e}^{-z}}} g(z)=1+e−z1。
python代码实现:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
合起来,我们得到逻辑回归模型的假设:
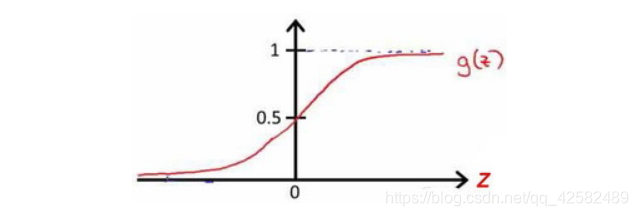
logistic函数的图像为
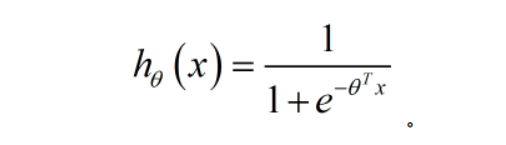
z趋向于负无穷大时,值越接近0;z趋向于正无穷大时,值越接近1。这样就可以使输出值在0到1之间。有了这个假设函数,就可以拟合数据了,根据给定的θ参数值,假设会做出预测。
h θ ( x ) h_\theta \left( x \right) hθ(x)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性, h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta \left( x \right)=P\left( y=1|x \ ;\theta \right) hθ(x)=P(y=1∣x ;θ),相应的负类的概率为 P ( y = 0 ∣ x ; θ ) P\left( y=0|x \ ; \theta \right) P(y=0∣x ;θ)。借助公式 P ( y = 1 ∣ x ; θ ) + P ( y = 0 ∣ x ; θ ) = 1 P\left( y=1|x \ ;\theta \right)+P\left( y=0|x \ ; \theta \right)=1 P(y=1∣x ;θ)+P(y=0∣x ;θ)=1 就可以根据正类求出负类的概率了。
决策边界
决策边界(Decision Boundary) 的概念能帮助我们更好地理解假设函数在计算什么

在逻辑回归中,我们这样预测:
当 h θ ( x ) > = 0.5 {h_\theta}\left( x \right)>=0.5 hθ(x)>=0.5 时,预测 y = 1 y=1 y=1。
当 h θ ( x ) < 0.5 {h_\theta}\left( x \right)<0.5 hθ(x)<0.5 时,预测 y = 0 y=0 y=0 。
根据logistic函数的图像,我们知道
z = 0 z=0 z=0 时 g ( z ) = 0.5 g(z)=0.5 g(z)=0.5
z > 0 z>0 z>0 时 g ( z ) > 0.5 g(z)>0.5 g(z)>0.5
z < 0 z<0 z<0 时 g ( z ) < 0.5 g(z)<0.5 g(z)<0.5
而 z = θ T x z={\theta^{T}}x z=θTx ,所以有:
θ T x > = 0 {\theta^{T}}x>=0 θTx>=0 时,预测 y = 1 y=1 y=1
θ T x < 0 {\theta^{T}}x<0 θTx<0 时,预测 y = 0 y=0 y=0
接下来让我们假设有一个模型(叉叉表示正样本,圆圈表示负样本),并且模型 h θ ( x ) h_\theta \left( x \right) hθ(x) 的参数 θ = [ − 3 1 1 ] \theta=\left[ \begin{matrix} {-3} \\ {1} \\ {1} \\ \end{matrix} \right] θ=⎣⎡−311⎦⎤
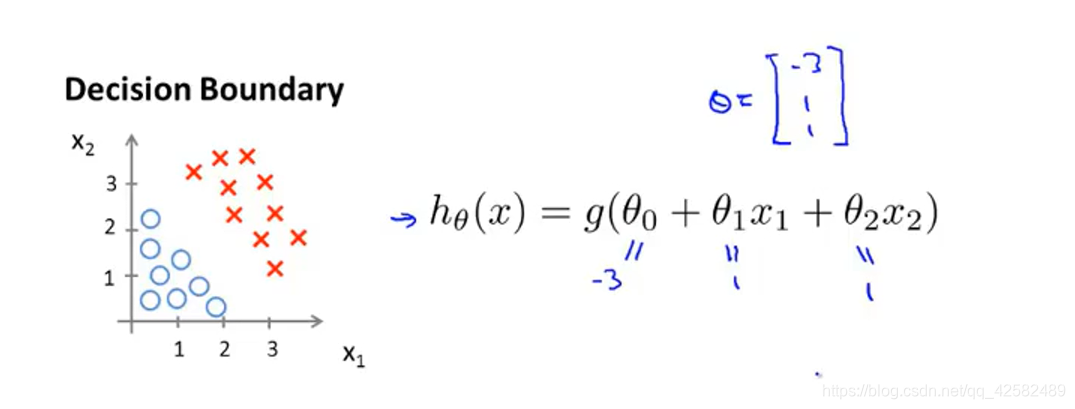
那么我们知道,当 − 3 + x 1 + x 2 ≥ 0 -3+{x_1}+{x_2} \geq 0 −3+x1+x2≥0,即 x 1 + x 2 ≥ 3 {x_1}+{x_2} \geq 3 x1+x2≥3时,模型将预测 y = 1 y=1 y=1。
我们可以绘制直线 x 1 + x 2 = 3 {x_1}+{x_2} = 3 x1+x2=3,这条线就是我们模型的决策边界,将预测为1的区域和预测为 0的区域分隔开。
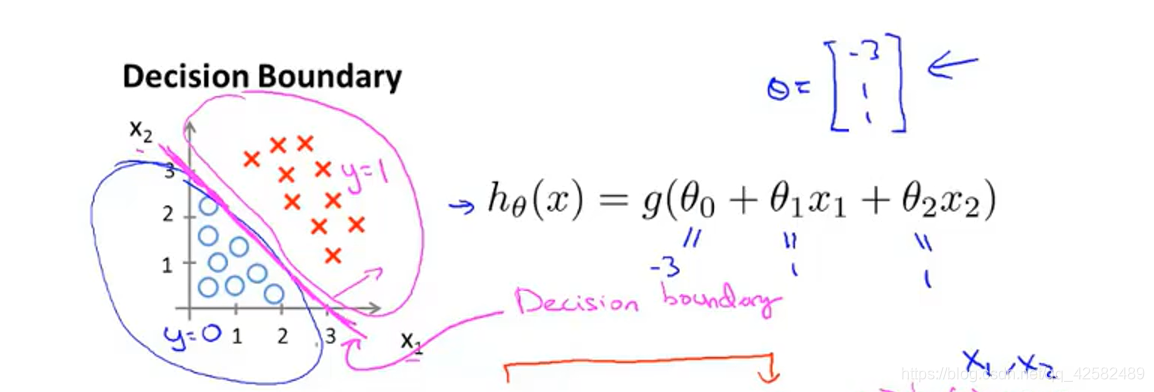
这条决策边界以及我们预测 y = 1 y=1 y=1 和 y = 0 y=0 y=0 的区域,它们都是假设函数的属性,取决于其参数。即使去掉了这些数据,它们依然存在且不会改变。
现在我们来看一个更复杂的例子,对于logistic回归,我们在特征中添加额外的高阶多项式项 x 1 2 {x_1}^2 x12、 x 2 2 {x_2}^2 x22,我们会在之后讨论怎么选择参数 θ \theta θ 的取值,假设现在我们已经知道了 θ = [ − 1 0 0 1 1 ] \theta=\left[ \begin{matrix} {-1} \\ {0} \\ {0} \\ {1} \\ {1} \\ \end{matrix} \right] θ=⎣⎢⎢⎢⎢⎡−10011⎦⎥⎥⎥⎥⎤

当 − 1 + x 1 2 + x 2 2 ≥ 0 -1+{x_1}^2+{x_2}^2 \geq 0 −1+x12+x22≥0,即 x 1 2 + x 2 2 ≥ 1 {x_1}^2+{x_2}^2 \geq 1 x12+x2








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 286
286

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








