欠拟合与正则化-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_42474833/article/details/107720162

本文探讨了在样本数量变化时，模型复杂度对欠拟合的影响，并分析了正则化参数λ如何影响模型的偏差与方差。通过学习曲线和验证曲线，我们能够调整模型复杂度和正则化强度，以找到最佳拟合。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

欠拟合图像
样本很小时，训练集可以较好拟合，一旦样本变多，过于简单的直线无法拟合数据，误差变大。对于交叉验证集而言，样本变多拟合效果自然更好，但是最终趋于跟训练集误差基本相同，因为都有大量的数据点无法拟合。
在这里插入图片描述

function [error_train, error_val] = learningCurve(X, y, Xval, yval,lambda)

m_train=size(X,1);
error_train=zeros(m_train,1);
error_val=zeros(m_train,1);
for i=1:m_train
    theta = trainLinearReg(X(1:i,:), y(1:i), lambda);
    %技巧 lambda为0计算误差
    error_train(i)=linearRegCostFunction( X(1:i,:), y(1:i),theta,0 );
    %注意训练集误差的计算方式 只算拟合时用到的数据
    error_val(i)=linearRegCostFunction( Xval,yval,theta,0 );%整个交叉验证集
end
end

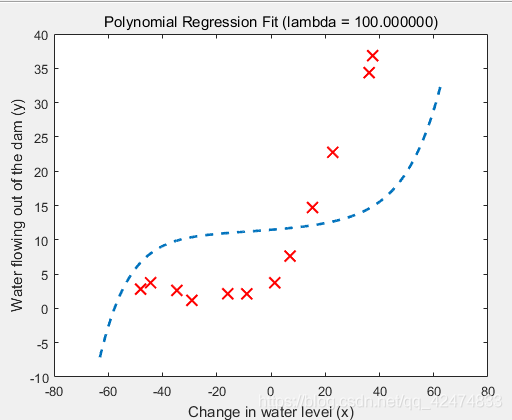
不同正则化参数 $\lambda$ 的影响：过大容易出现高偏差，过小容易出现高方差。

在这里插入图片描述

function [lambda_vec,error_train, error_val] = validationCurve(X, y, Xval, yval)

lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
error_train=zeros(length(lambda_vec),1);
error_val=zeros(length(lambda_vec),1);
for i=1:length(lambda_vec)
    lambda=lambda_vec(i);
    theta = trainLinearReg(X, y, lambda);
    %技巧 lambda为0计算误差
    error_train(i)=linearRegCostFunction( X, y,theta,0 );
    %注意训练集误差的计算方式 只算拟合时用到的数据
    error_val(i)=linearRegCostFunction( Xval,yval,theta,0 );%整个交叉验证集
end
end

在这里插入图片描述
其他函数

function X_poly = polyFeatures(X, p)
%特征向多维映射
m=size(X,1);
X_poly=zeros(m,p);
for i=1:p
    x_temp=X.^i;
    X_poly(:,i)=x_temp;
end;
end

function [J,grad] = linearRegCostFunction( X,y,theta,lambda )
%线性回归的代价函数

m=size(X,1);
J=0;
J=sum( ((X*theta)-y).^2 )/(2*m)+lambda/(2*m)*sum(theta(2:end,1).^2);

grad=zeros(size(theta,1));
%grad(1)=1/m*X(:,1)'*((X*theta)-y);
%grad(2:end)=1/m*X(:,2:end)'*((X*theta)-y)+lambda/m*theta(2:end,1);
%最佳向量化
grad=1/m*X'*((X*theta)-y)+lambda/m*[0;theta(2:end,1)];%相当于x0不进行正则化
end

function [theta] = trainLinearReg(X, y, lambda)
%迭代寻找参数

initial_theta = zeros(size(X, 2), 1); 
costFunction = @(t) linearRegCostFunction(X, y, t, lambda);
options = optimset('MaxIter', 200, 'GradObj', 'on');
theta = fmincg(costFunction, initial_theta, options);

end