

特征缩放 须返回均值和标准差,因为在预测时,要对输入的数据进行相同的特征缩放才能预测
function [ X_norm ,miu,sigma] = featureNormalize( X )
%两个特征值的数值相差很大 特征缩放
X_norm=X;
miu=zeros(1,size(X,2));
sigma=zeros(1,size(X,2));
miu=mean(X,1);%求均值
sigma=std(X,0,1);%求方差
%对 仍然局限于两个特征值
% X(:,1)=(X(:,1)-miu(1))/sigma(1);
% X(:,2)=(X(:,2)-miu(2))/sigma(2);
for i=1:size(X,2)
X_norm(:,i)=(X(:,i)-miu(i))/sigma(i);
end
end
多元代价函数
function J = computeCostMulti(X,y,theta)
m=length(y);
J=0;
J=sum((X*theta-y).^2)/(2*m);
end
多元梯度下降
function [ theta,J ] = gradientDescentMulti( X,y,theta,alpha,iterations )
%重点是梯度下降参数更新方程的向量化
m=length(y);
J=zeros(iterations,1);
for i=1:iterations
%以下代码正确但只局限于两个特征量
theta0=theta(1);
theta1=theta(2);
theta2=theta(3);
x1=X(:,2);
x2=X(:,3);
theta0=theta0-alpha* sum((X*theta-y))/m;
theta1=theta1-alpha* sum((X*theta-y).*x1)/m;
theta2=theta2-alpha* sum((X*theta-y).*x2)/m;
theta=[theta0;theta1;theta2];
%选择一种更好的向量化的方式
%X*theta-y是m*1的向量 X是m*3的向量 -->3*1向量 含义是X的每一列与X*theta-y相乘求和
theta=theta-alpha*X'*(X*theta-y)/m;
J(i)=computeCostMulti(X,y,theta);
end
正则方程解法
function [ theta ] = normalEqn( X,y )
theta=zeros(size(X,2),1);%初始化大小
theta=pinv(X'*X)*X'*y;
end
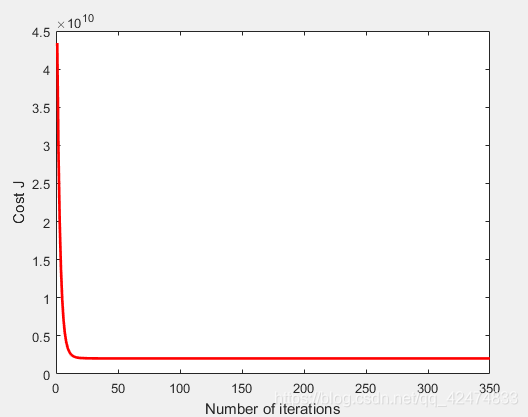




 本文详细介绍了机器学习中特征缩放的重要性及其实施方法,包括计算均值和标准差,以及如何使用这些参数进行数据标准化。此外,还探讨了多元线性回归的代价函数和梯度下降算法,以及正则方程解法。
本文详细介绍了机器学习中特征缩放的重要性及其实施方法,包括计算均值和标准差,以及如何使用这些参数进行数据标准化。此外,还探讨了多元线性回归的代价函数和梯度下降算法,以及正则方程解法。
















 776
776










