线性回归模型笔记整理8 - 多项式扩展 解决线性回归模型欠拟合问题

1. 尝试线性回归模型解决欠拟合(with codes)

• 尝试用线性回归模型，来解决欠拟合问题，效果不好
  我们可以使用线性回归模型来拟合数据，然而，在现实中，数据未必总是线性（或接近线性）的。当数据并非线性时，直接使用LinearRegression的效果可能会较差，产生欠拟合。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

mpl.rcParams["font.family"] = "SimHei"
mpl.rcParams["axes.unicode_minus"] = False

x = np.linspace(0, 10, 50)
# 真实的数据分布。该分布是非线性的。
y = x * np.sin(x)
# np.newaxis 表示进行维度的扩展，可以认为是增加一个维度，该维度为1。
# 此种方式也可以通过reshape方法来实现。
X = x[:, np.newaxis]
lr = LinearRegression()
lr.fit(X, y)
# 输出在训练集上的分值。查看线性回归LinearRegression在非线性数据集上的拟合效果。
print(lr.score(X, y))
# 将样本数据以散点图进行绘制。
plt.scatter(x, y, c="g", label="样本数据")
# 绘制预测值（模型的回归线）
plt.plot(X, lr.predict(X), "r-", label="拟合线")
plt.legend()
plt.show()
# 结果：R ^ 2值为0.05908132146396671，模型在训练集上表现非常不好，产生欠拟合。

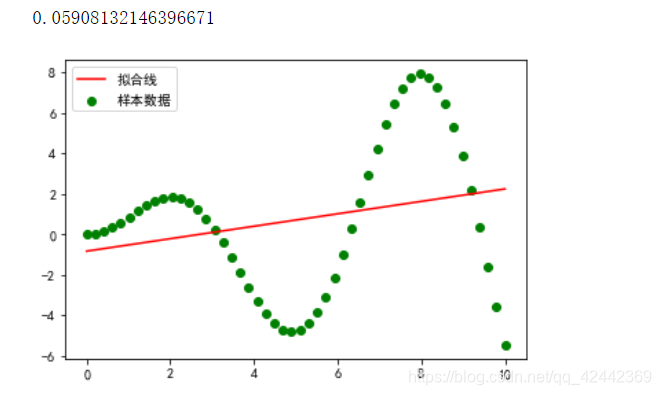
程序解释

是真实线，还没有加噪声。就是想看，非线性再线性上表现怎么样。

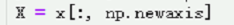
表示要进行维度的扩展
可以认为是增加一个维度，该维度为1
Why要增加一个维度？
意味着x能否送到fit？不能
一维不能

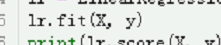
X要变成二维
现在是 50，
变成50,1
之前是reshape
现在变成

# x = np.linspace(0, 10, 50)
# print(x.shape)
# print(x[:, np.newaxis].shape)

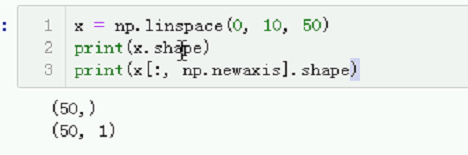
习惯大写

欠拟合 是不涉及未知数据的，欠拟合是训练集相关
跟未知数据无关

Eg. 模拟题都做不好

看下效果

将样本数据以散点图进行绘制

真实值

还差一个预测值，就是一条回归线，模型的回归线。

Show()在jupyter里面可以不加，pycharm里面得加，这也是 sinx x

综上看，这个拟合效果不好。所以线性回归 对非线性 拟合效果不好。相当于蒙。

因为线性回归是直的，在训练集上表现不好，产生欠拟合现象，$R^2$ 值很低。

2. 欠拟合怎么办？引入多项式扩展

此时，我们可以尝试使用多项式扩展来进行改进。
多项式扩展，可以认为是对现有数据进行的一种转换，通过将数据映射到更高维度的空间中，该模型就可以拟合更广泛的数据。
假设，我们有如下的二元线性模型：

$\hat{y}=w_0+w_1{x}_1+w_2{x}_2$

如果该模型的拟合效果不佳，我们就可以对该模型进行多项式扩展。例如，我们进行二项式扩展（也可以进行更高阶的扩展），结果为：

$\hat{y}=w_0+w_1{x}_1+w_2{x}_2+w$