day32【代码随想录】回溯之N皇后、N皇后||、解数独、有效的数独

---

前言

1、N皇后、
2、N皇后||、
3、解数独、
4、有效的数独

---

一、N皇后（力扣51）

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

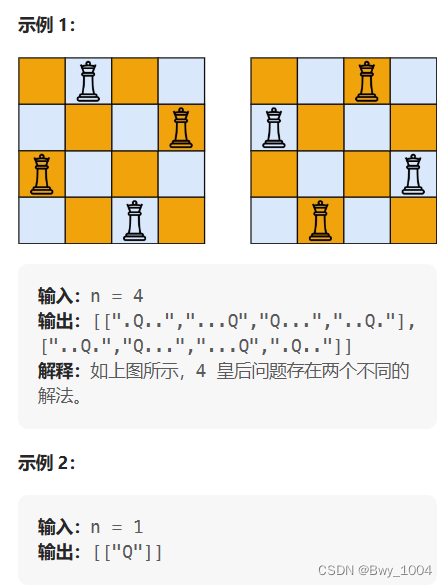
思路：

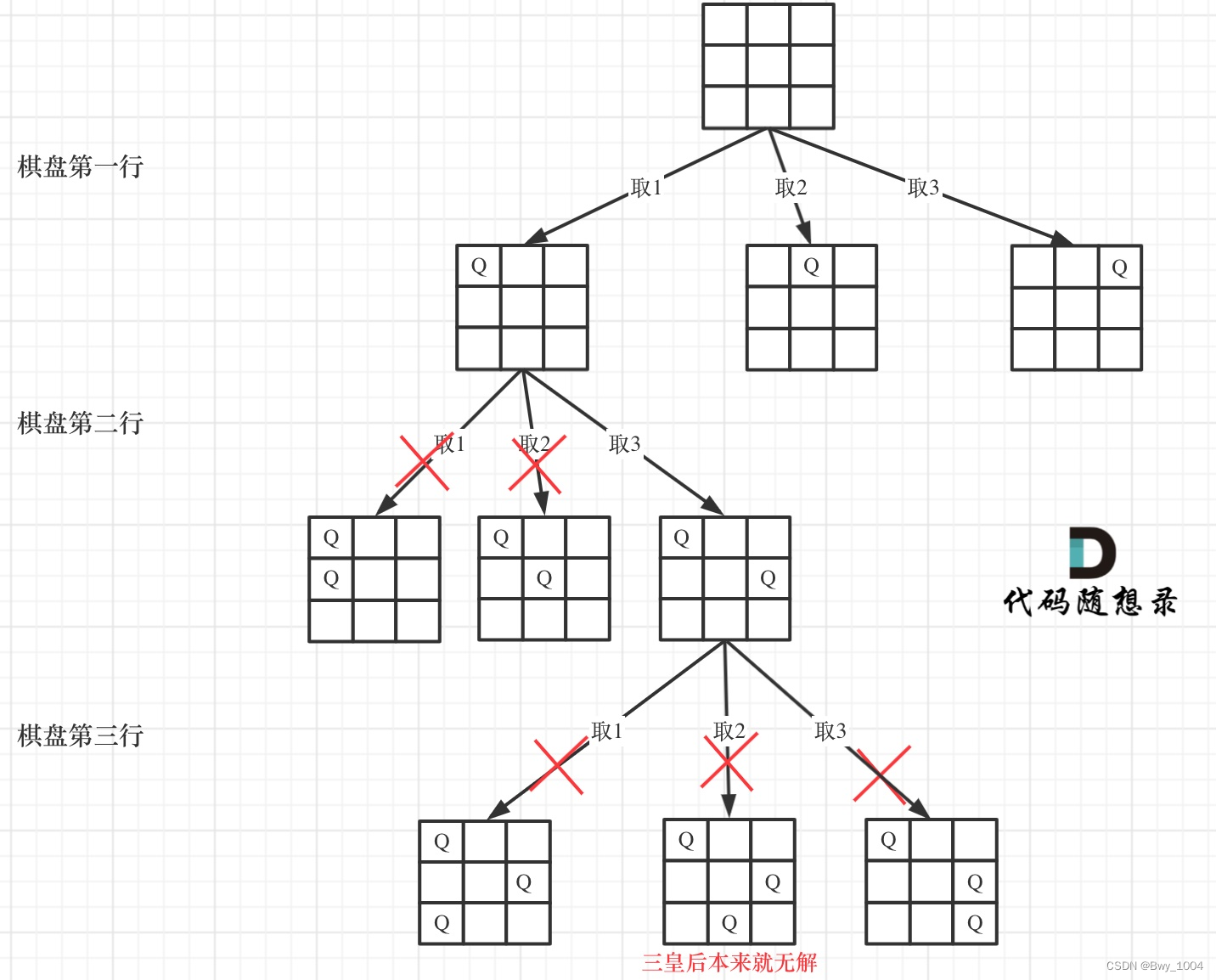
根据树形结构+回溯模板搭出框架

递归结束条件
if(row==n) //收集结果
而这里的收集结果 需要将二维数组 转换为list结果集。

单层递归逻辑

for循环里边的i实际上是棋盘中的列
递归层数实际上是棋盘中的行
需要判断棋盘当前位置存放皇后是否合法

class Solution {
    List<List<String>> res= new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char[][] chessBoard = new char[n][n];
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                chessBoard[i][j]='.';
            }
        }
        backTracking(chessBoard,n,0);
        return res;
    }
    public void backTracking(char[][] chessBoard,int n,int row){
        if(row==n){
            //收集结果
            res.add(Array2List(chessBoard));
        }
        for(int i=0;i<n;i++){
            if(isValid(chessBoard,row,i,n)){
                chessBoard[row][i]='Q';
                backTracking(chessBoard,n,row+1);
                //回溯
                chessBoard[row][i]='.';
            }
        }
    }
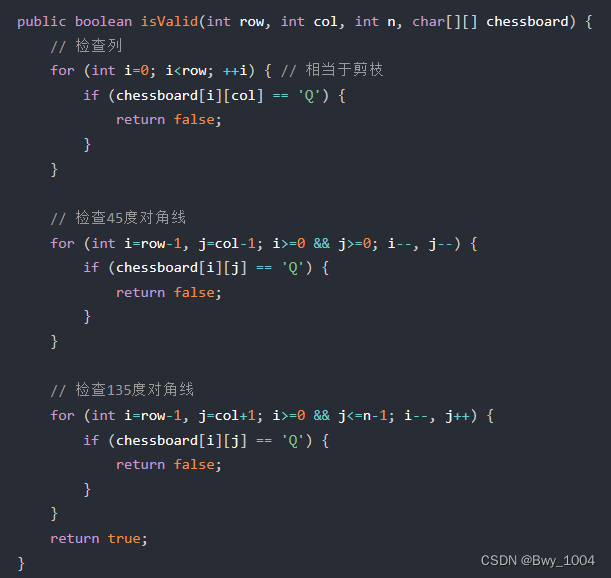
    public boolean isValid(char[][] chessBoard,int row,int col,int n){
        //检查列
        for(int i=0;i<row;i++){
            if(chessBoard[i][col]=='Q')
                return false;
        }
        //检查45度
        for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){
            if(chessBoard[i][j]=='Q')
                return false;
        }
        //检查145度
        for(int i=row-1,j=col+1;i>=0&&j<=n-1;i--,j++){
            if(chessBoard[i][j]=='Q')
                return false;
        }
        return true;
    }
    public List Array2List(char[][] chessBoard){
        List<String> list = new ArrayList<>();

        for(char[] c:chessBoard){
            list.add(String.copyValueOf(c));
        }
        return list;
    }
}

二、N皇后||（力扣52）

给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

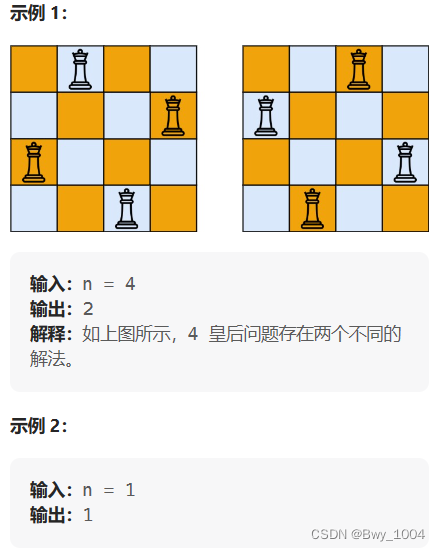
思路：
很明显，在N皇后的基础上，return res.size();即可解决N皇后||

class Solution {
    List<List<String>> res = new ArrayList<>();
    public int totalNQueens(int n) {
        char[][] chessBoard = new char[n][n];
        for(char[] c:chessBoard){
            Arrays.fill(c,'.');
        }
        backTracking(chessBoard,n,0);
        return res.size();

    }
    public void backTracking(char[][] chessBoard,int n,int row){
        if(row==n){
            //收集结果
            res.add(Array2List(chessBoard));
            return ;
        }
        for(int i=0;i<n;i++){
            if(isValid(chessBoard,row,i,n)){
                chessBoard[row][i] = 'Q';
                backTracking(chessBoard,n,row+1);
                //回溯
                chessBoard[row][i] = '.';
            }
        }
    }
    public List Array2List(char[][] chessBoard){
        List<String> list = new ArrayList<>();
        for(char[] c:chessBoard){
            list.add(String.copyValueOf(c));
        }
        return list;
    }
    public boolean isValid(char[][] chessBoard,int row,int col,int n){
        //检查列
        for(int i=0;i<=row;i++){
            if(chessBoard[i][col]=='Q')
                return false;
        }
        //检查45度
        for(int i=row-1,j=col-1;i>=0&& j>=0;i--,j--){
            if(chessBoard[i][j]=='Q')
                return false;
        }
        //检查135度
        for(int i=row-1,j=col+1;i>=0&&j<=n-1;i--,j++){
            if(chessBoard[i][j]=='Q')
                return false;
        }
        return true;
    }
}

三、解数独（力扣37）

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）
数独部分空格内已填入了数字，空白格用 ‘.’ 表示。


思路：

首先递归函数的返回值不再是void 而是定义为Boolean类型，原因在于其他回溯问题都是返回多种结果，遍历完所有的结果最后return；而数独只要走通一个分支结束即可。不需要再找其他结果
public boolean backTracking(char[][] board)
放return false 是有讲究的。
如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！
return true
遍历完没有返回false，说明找到了合适棋盘位置了

判断在i行j列存放k字符是否合法：
检查行

检查列

检查九宫格

注意这里九宫格的起始行和起始列的计算方式：
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3

class Solution {
    public void solveSudoku(char[][] board) {
        backTracking(board);
    }
    public boolean backTracking(char[][] board){
        for(int i=0;i<9;i++){//行
            for(int j=0;j<9;j++){ //列
                if(board[i][j]=='.'){//需要进行处理
                    for(char k='1';k<='9';k++){
                        if(isValid(i,j,k,board)){
                            board[i][j]=k;
                            boolean result = backTracking(board);
                            if(result==true) return true;
                            board[i][j]='.';
                        }
                    }
                    //9个数都尝试了 都不行
                    return false;
                }
            }
        }
        //都遍历完之后发现都合法
        return true;
    }
    public boolean isValid(int row,int col,char k,char[][] board){
        //行是否合法
        for(int j=0;j<9;j++){
            if(board[row][j]==k)
                return false;
        }
        //检查列是否合法
        for(int i=0;i<9;i++){
            if(board[i][col]==k)
                return false;
        }
        //检查9宫格
        int startRow = (row/3)*3;
        int startCol = (col/3)*3;
        for(int i=startRow;i<startRow+3;i++){
            for(int j=startCol;j<startCol+3;j++){
                if(board[i][j]==k)
                    return false;
            }
        }
        return true;
    }
}

四、有效的数独（力扣36）

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

思路：
其实就是解数独中调用的isValid函数

class Solution {
    public boolean isValidSudoku(char[][] board) {
        for(int i=0;i<9;i++){
            for(int j=0;j<9;j++){
                if(board[i][j]!='.'){
                    if(!isValid(i,j,board[i][j],board))
                        return false;
                }
            }
        }
        return true;
    }
    public boolean isValid(int row,int col,char val,char[][] board){
        board[row][col]='.';
        //检查行
        for(int j=0;j<9;j++){
            if(board[row][j]==val)
                return false;
        }
        //检查列
        for(int i=0;i<9;i++){
            if(board[i][col]==val)
                return false;
        }
        //检查九宫格
        int startRow = (row/3)*3;
        int startCol = (col/3)*3;
        for(int i=startRow;i<startRow+3;i++){
            for(int j=startCol;j<startCol+3;j++){
                if(board[i][j]==val)
                    return false;
            }
        }
        board[row][col]=val;
        return true;
    }
}

---