数据结构知识整理18查找之线性表查找

查找

查找（又称检索）：指在某种数据结构中找出满足给定条件的元素。

被查找的对象是由一组元素组成的表或文件，而每个元素由若干个数据项组成，假设每个元素都有一个能唯一标识该元素的关键字，在这种条件下，查找的定义是：给定一个值k，在含有n个元素的表中找出关键字等于k的元素。若找到，则查找成功，返回该元素的信息或该元素在表中的位置；否则查找失败，返回相关的指示信息。

采用何种查找方法，取决于使用哪种数据结构来表示“表”，即表中元素是何种方式组织的。为提高查找效率，常用特殊的数据结构来组织表，或对表事先进行诸如排序等运算。因此在研究各种查找方法时，首先必须弄清这些方法所针对的数据结构时什么，以及关键字的次序有何要求，如是无序集合还是有序集合。

若在查找的同时对表做修改运算（如插入和删除），则相应的表称为动态查找表，反之称为静态查找表。

若整个查找过程都在内存进行，则称之为内查找，反之要访问外存，称为外查找。

由于查找运算的主要运算是关键字的比较，所以通常把查找过程中对关键字的平均比较次数（也称为平均查找长度）作为衡量一个查找算法效率优劣的标准。平均查找长度ASL（Average Search Length）

定义为：                       ASL=i=1npici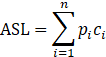

其中，n是所查找表中元素个数，pi是查找第i个元素的概率，一般认为每个元素的查找概率相等，即pi=1/n（1≤i≤n），ci是找到第i个元素所需的比较次数。

线性表查找

线性表是表组织方式中最简单的一种。

顺序查找

顺序查找是一种最简单的查找方法。它的基本思路是：从表的一端开始，顺序扫描线性表，依次将扫描到的关键字和给定值k相比较，若当前扫描的关键字与k相等，则查找成功；若扫描结束，仍未找到关键字等于k的元素，则查找失败。

优点：算法简单，无结构要求。缺点：查找效率低。
 

折半查找

折半查找（又称二分查找）是一种效率较高的查找方法。要求线性表是有序表。

假设有序表递增有序。折半查找的基本思路是：设R[low…high]是当前的查找区间，首先确定该区间的中点位置mid=（low+high）/2向小取整，然后将待查的k值与R[mid].key比较：

1. 若R[mid].key=k，则查找成功并返回该元素的逻辑序号；
2. 若R[mid].key>k，则由表的有序性可知R[mid..n-1].key均大于k，因此若表中存在关键字等于k的元素，则该元素必定是在位置mid的左子表R[0…mid-1]中，故新的查找区间是左子表R[0…mid-1]；
3. 若R[mid].key<k，则要查找的k必在mid的右子表R[mid+1…n-1]中，即新的查找区间是右子表R[mid+1…n-1]。

下一次查找是针对新的查找区间进行的。每经过一次查找，不成功则查找区间缩小一半。这一过程重复直至找到关键字为k的元素，或者直至当前的查找区间为空（即查找失败）为止。

折半查找过程可用二叉树描述，把当前查找区间的中点位置上的元素作为根，左子表和右子表中的元素分别作为根的左子树和右子树，由此得到二叉树，称为描述折半查找的判定树或比较树。树的形态只与表元素个数n相关。

成功的折半查找过程恰好是一条从判断树的根到被查元素的路径，关键字的比较次数恰为所查找元素在树中的层数。在查找失败时所需比较的关键字个数不超过判定树的深度。

优缺点：虽然折半查找的效率高，但是需要将表按关键字排序，而排序本身费时，高效率排序也需要花费O（nlog2n）的时间。另外折半查找需要确定查找的区间，因此只适用于顺序存储结构，不适用于链式存储结构。为保持表的有序性，在顺序结构里插入和删除都必须移动大量的元素，因此，折半查找适用于一经建立就很少改动、而又经常需要查找的线性表。适用于静态查找表。
 

索引存储结构和分块查找

索引存储结构是在存储数据的同时，还建立附加的索引表。索引表中的每一项称为索引项，索引项的一般形式是：                         （关键字，地址）

关键字唯一标识一个节点，地址是指向该关键字对应节点的指针，也可以是相对地址。

在索引存储结构中进行关键字查找时，可以先在索引表中快速查找（因为索引表中按关键字有序排列，可以采用折半查找）到相应的关键字，然后通过地址找到节点表中对应的节点。线性结构采用索引存储后，可以对节点进行随机访问。在进行插入、删除运算时，由于只需修改索引表中相关节点的存储地址，而不必移动存储在节点表中的节点，所以仍可保持较高的运算效率。缺点是为建立索引表而增加的时间和空间的开销。

分块查找（又称索引顺序查找），它是一种性能介于顺序查找和折半查找之间的查找方法。它要求按如下的索引方式来存储线性表：将表R[0…n-1]均分为b块，前b-1块中元素个数为s=n/b向上取整，最后一块即第b块的元素个数小于等于s；每一块中的关键字不一定有序，但前一块中的最大关键字必须小于后一块中的最小关键字，即要求表是“分块有序”的；抽取各块的最大关键字及起始位置构成一个索引表IDX[0…b-1]，即IDX[i]（0≤i≤b-1）中存放着第i块的最大关键字及该块在表R中的起始位置。由于表R是分块有序的，所以索引表是一个递增有序表。

分块查找基本思路：首先查找索引表，因为索引表是有序表，故可采用折半查找或顺序查找，以确定待查的元素在哪一块；然后在已确定的块中进行顺序查找（块内元素无序）。

确定块用折半查找时，块的长度越小越好，顺序查找时候，块元素个数为根号n最好。

分块查找的主要代价是增加一个索引表的存储空间和延长建立索引表的时间。