博弈论..

原创已于 2024-06-11 11:18:08 修改 · 305 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#矩阵 #线性代数

于 2021-05-16 20:12:45 首次发布

Algorithm 专栏收录该内容

10 篇文章

订阅专栏

本文深入解析博弈论基础，包括纳什均衡、纯策略与混合策略、囚徒困境、占优策略等内容，以小鸡游戏和硬币游戏为例，探讨如何找到最优策略。通过硬币游戏揭示没有纯策略纳什均衡的情况，强调混合策略在零和游戏中的应用。

B站原视频链接：博弈论入门（Game Theory）【纳什均衡、囚徒困境、纯策略纳什均衡、占优策略】_哔哩哔哩_bilibili

Minimax算法及实例分析_我的专栏-优快云博客_minimax算法

1. 偏好（Preference）

定义

性质

2. 效用（Untility）

定义

3. 偏好与效用

4. 策略集合（Strategy Set）

策略集合是由玩家能够施行的策略所组成的集合。

例：游戏剪刀、石头、布的策略集合是{ 出剪刀 , 出石头 , 出布 }

5. 收益矩阵（Utility Matrix）

玩家在游戏中，每一个策略所对应的收益所组成的矩阵例：游戏剪刀、

石头、布的收益矩阵为：

6. 双人正则形式博弈（2-People Normal-Form Game）

性质：正则形式博弈采用矩阵来陈述博弈的效用（得分、收益）。

例如：假设有小明（I）和小刚（II）两位参与者，得分矩阵分别为：

可以理解为小鸡游戏（The Chicken Game），小明和小刚的策略集合都是{选鸡，选鹰}。

·显然，这个游戏最好的结果是小明 (I) 和小刚 (II)同时选择“鸡”。这样，他们两人都可以得 4 分。

·但是，如果小明选“鸡”的话，小刚就应该选“鹰”，这样他可以得 5 分而不是 4 分。我们把小刚当他知道小明“选鸡”的时候“选鹰”，称为他的一个最优策略，反之亦然（即另一个最优策略是当知道小明“选鹰”的时候“选鸡”）。

7. 纳什均衡（Nash Equilibrium）

在博弈中，如果每个参与者在已知其他参与者的策略的情况下，采用最优策略来应对，

那么我们就达到了一个纳什均衡，或者找到了一个纳什均衡解，同时也意味着没有人能

通过改变自己的策略，获得更好的结果（得分、效用或者收益）。

在小鸡游戏中，（鸡，鹰）和（鹰，鸡）是纳什均衡。

Me：（鸡，鹰）是纳什均衡即当小明是鸡时，小刚应该选择鹰，相反小刚是鹰时，小明应该选择鸡。同时意味着如果小明（或小刚）不变策略，则小刚（或小明）无法通过改变自己的策略来获得更好的结果。

8. 纯策略纳什均衡（Pure Strategy Nash Equilibrium）

纯策略纳什均衡下，参与者只能使用策略集合中的一条策略。

·纯策略纳什均衡可能存在多个，也可能不存在。

9. 硬币正反游戏的例子（原文：三十分钟理解博弈论“纳什均衡” -- Nash Equilibrium_Bin 的专栏-优快云博客_纳什均衡）

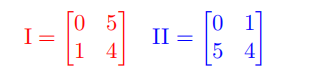
你正在图书馆枯坐，一位陌生美女主动过来和你搭讪，并要求和你一起玩个数学游戏。美女提议：“让我们各自亮出硬币的一面，或正或反。如果我们都是正面，那么我给你3元，如果我们都是反面，我给你1元，剩下的情况你给我2元就可以了。”那么该不该和这位姑娘玩这个游戏呢？

每一种游戏依具其规则的不同会存在两种纳什均衡，一种是纯策略纳什均衡，也就是说玩家都能够采取固定的策略(比如一直出正面或者一直出反面)，使得每人都赚得最多或亏得最少；或者是混合策略纳什均衡，而在这个游戏中，便应该采用混合策略纳什均衡。

假设我们出正面的概率是x，反面的概率是1-x，美女出正面的概率是y，反面的概率是1-y。为了使利益最大化，应该在对手出正面或反面的时候我们的收益都相等，由此列出方程就是

3x + (-2)(1-x)=(-2) * x + 1*( 1-x )——解方程得x=3/8；同样，美女的收益，列方程-3y + 2( 1-y)= 2y+ (-1) * ( 1-y)——解得y也等于3/8。

于是，我们就可以算美女每次的期望收益是：（1-y）(2x-(1-x)) + y(-3x+2(1-x)) = 1/8元，也就是说，双方都采取最优策略的情况下，平均每次美女赢1/8元。

其实只要美女采取了(3/8,5/8)这个方案，不论你再采用什么方案，都是不能改变局面的。如果全部出正面，每次的期望收益是 (3+3+3-2-2-2-2-2)/8=-1/8元；如果全部出反面，每次的期望收益也是(-2-2-2+1+1+1+1+1)/8=-1/8元。比如你用完全随机（1/2，1/2）策略，收益是1/2(3/8 * 3 + 5/8 * (-20)) + 1/2(3/8 * (-2) + 5/8 * 1) = -1/8；实际上，不论你用什么策略，你的收益都是-1/8，也就是说，随便玩一种策略，你都是在纳什均衡状态中的，所以，这个把戏你随便怎么玩，都是亏的。

这个例子中没有纯策略纳什均衡的，因为只出一种策略，肯定有一方要亏钱，所以并不是其均衡状态（明明只要换一边就可以赚钱了，所以不是最佳策略）；而混合纳什均衡是存在的，事实上，Nash告诉我们“每个参与者都只有有限种策略选择、并允许混合策略的前提下，纳什均衡一定存在”，如果美女出(3/8,5/8)这个方案，另一边任何玩法都是期望收益一样的，也就满足了纳什均衡的条件。

Me：鸡鹰游戏中（鸡，鹰）和（鹰，鸡）都是纯策略纳什均衡。

10. 囚徒困境（Prisoner's Dilemma）

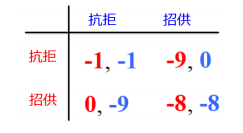
占优策略（Dominant Strategy）：在选择策略时，有一个策略的效用总是大于其他所有策略的效用时，我们把这类策略称为占优策略(Dominant Strategy)。

占优策略纳什均衡（Dominant Strategy Nash Equilibrium）：当所以参与者的最优回应是选择他们的占优策略时，这时达到的纳什均衡称为占优策略纳什均衡(Dominant Strategy Nash Equilibrium)。

囚徒困境中，招供是占优策略：因为无论A抗拒还是招供，B招供是最好的选择，反之亦然。

两个囚徒均选择其占优策略即（招供，招供）则达到了占优策略纳什均衡。

11. 课后题

没有纯策略纳什均衡。

如果 P 1 选 T 的话， P 2 会选择 R 。而现在 P 1 知道 P 2 选 R ，那么 P 1就会改选 B 。但是 P 2 知道 P 1 改选 B ，那么 P 2 就会改选 L 。于是 P 1 知道 P 2 改选 L的话，就会再改，选 T 。此时 P 2 知道 P 1 选 T 的话，就会从选 L 换成选 R，是成为一个循环，没有稳定的最优回应。所以没有纯策略纳什均衡。

12. 混合策略纳什均衡（Mixed Strategy Nash Equilibrium）