神经网络中的神经元
神经元数学模型
人工神经网络是一个用户大量简单处理单元经广泛链接而成的人工网络, 是对人脑的神经网络的抽象和模拟. 我们知道, 人脑的神经系统的基本的单位是神经元, 所以建立人工神经网络的首先要做的是对神经元的抽象, 建立神经元的数学模型.
早在1943年, 神经元的数学模型被提出, 之后又陆陆续续提出了上百种神经元模型, 下面是一种常用的神经元模型:
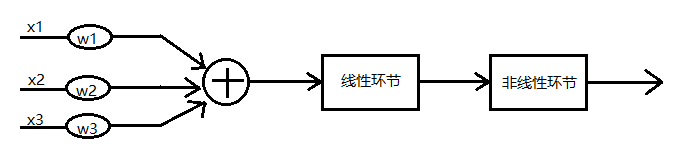
在这张图中, 我们可以看到这个神经元有三个输入, 一个输出, 这很像我们正常的神经元的树突和轴突:

在我们正常的神经元细胞中, 信息从树突输入, 经过细胞体处理后从轴突输出. 我们可以看到, 在神经元模型中有一个线性环节和一个非线性环节, 这就是信息处理的部分, 也就是模拟了细胞体的功能.
线性环节,就是将输入的数
x
1
.
.
.
x
n
x_1...x_n
x1...xn乘以他们对应的权数
w
1
.
.
.
w
n
w_1...w_n
w1...wn再相加
a
=
w
1
x
1
+
.
.
.
+
w
n
x
n
+
b
a=w_1x_1+...+w_nx_n+b
a=w1x1+...+wnxn+b, 得到我们线性环节的输出
a
a
a, 非线性环节, 就是将我们再线性环节输出的数
a
a
a放到我们准备好的非线性函数
y
=
y
(
x
)
y=y(x)
y=y(x)中, 得到这个神经元的最终输出值
y
y
y.
为什么需要非线性函数呢? 因为如果我们不加入非线性函数的话, 得到的只是输入线性的结合, 那么无论神经网络有多复杂, 我们能把他合并为一个线性计算, 而加入了非线性环节, 我们的神经元就能获得更多的可能.
那么怎么选择非线性部分的函数呢? 首先我们可以想到生物的神经元具有两种常规的工作状态: 兴奋与抑制, 这让我们很容易想到0和1, 我们用0来模拟抑制, 用1来模拟兴奋, 那么我们就会想到用阶跃函数来作为神经元的非线性部分
f
(
x
)
=
{
1
x
≥
0
0
x
<
0
f(x)=\begin{cases} 1 & x\geq0 \\ 0 & x<0 \\ \end{cases}
f(x)={10x≥0x<0
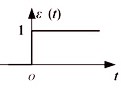
这样我们就解决了非线性部分的函数了
那么, 神经元怎么训练呢?
首先明确一点, 神经元的训练就是调节
w
1
w_1
w1…
w
n
w_n
wn和b的值, 是神经元的计算结果越来越趋近于我们所期待的输出值
我们将
y
y
y定义为神经元计算出来的值,
y
s
y_s
ys为理想的输出值, 那么误差函数为
e
=
(
y
s
−
y
)
2
e=(y_s-y)^2
e=(ys−y)2, 那我们怎么知道该怎么调整
w
w
w和
b
b
b的值呢? 其实我们可以是我们的误差函数
e
e
e对
w
w
w和
b
b
b求导, 然后往导数小的地方调整就可以了, 那么问题来了, 阶跃函数的导数不连续啊, 这样不方便计算啊. 所以, 我们得还一个非线性函数了.
非线性函数和梯度下降
实际上, 常用的非线性函数有很多, 在这里我们选择的函数叫做
s
i
g
n
m
o
i
d
signmoid
signmoid函数.
s
(
x
)
=
1
/
(
1
+
e
−
x
)
s(x)=1/(1+e^{-x})
s(x)=1/(1+e−x)
这个函数有一个好处, 就是可以用它本身来表示他的导数:
d
s
(
x
)
/
d
x
=
s
(
x
)
(
1
−
s
(
x
)
ds(x)/dx = s(x)(1-s(x)
ds(x)/dx=s(x)(1−s(x)
这又进一步简化了我们的计算. 那么, 接下来我们就推导我们的训练公式吧:
首先我们可以轻易地得到:
d
e
/
d
w
=
d
(
y
s
−
y
)
2
de/dw=d(y_s-y)^2
de/dw=d(ys−y)2
通过链式法则得出:
d
e
/
d
w
=
(
d
e
/
d
y
)
(
d
y
/
d
w
)
de/dw=(de/dy)(dy/dw)
de/dw=(de/dy)(dy/dw)
将
e
=
(
y
−
y
s
)
2
e=(y-y_s)^2
e=(y−ys)2带入得:
d
e
/
d
w
=
−
2
(
y
s
−
y
)
(
d
y
/
d
w
)
de/dw=-2(y_s-y)(dy/dw)
de/dw=−2(ys−y)(dy/dw)
同样的我们可以由链式法则得出:
d
y
/
d
w
=
(
d
y
/
d
a
)
/
(
d
a
/
d
w
)
dy/dw=(dy/da)/(da/dw)
dy/dw=(dy/da)/(da/dw)
前面我们可知:
d
y
(
a
)
/
d
a
=
s
(
a
)
(
1
−
s
(
a
)
)
dy(a)/da = s(a)(1-s(a))
dy(a)/da=s(a)(1−s(a))
所以:
d
e
/
d
w
=
−
2
(
y
s
−
y
)
s
(
a
)
(
1
−
s
(
a
)
)
de/dw=-2(y_s-y)s(a)(1-s(a))
de/dw=−2(ys−y)s(a)(1−s(a))
其中
a
=
w
1
x
1
+
.
.
.
+
w
n
x
n
+
b
a=w_1x_1+...+w_nx_n+b
a=w1x1+...+wnxn+b, 为了方便我们减少几个变量:
a
=
w
x
+
b
a=wx+b
a=wx+b, 那么可得:
d
e
/
d
w
=
−
2
(
y
s
−
y
)
s
(
w
x
+
b
)
(
1
−
s
(
w
x
+
b
)
)
x
de/dw=-2(y_s-y)s(wx+b)(1-s(wx+b))x
de/dw=−2(ys−y)s(wx+b)(1−s(wx+b))x
这样我们的公式就求出来了, 之后只要用
w
n
e
w
=
w
o
l
d
−
α
∗
d
e
/
d
w
w_{new}=w_{old}-α*de/dw
wnew=wold−α∗de/dw就可以了, 其中
α
α
α是学习率, 为0到1之间的值, 用来调节
w
w
w变化的强度, 保证不会越过我们所需要的最佳值.
这种方法被称为梯度下降
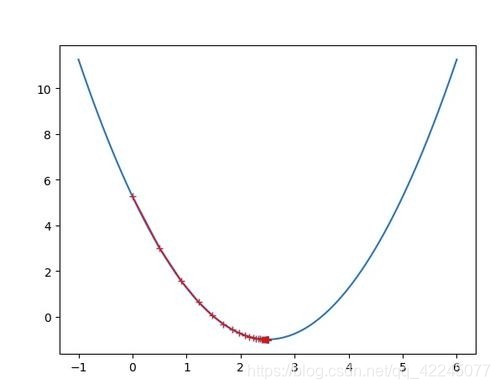
在这个函数中, 横坐标为
w
w
w, 纵坐标为误差, 当误差最小时, 关于
w
w
w的导数为0, 当导数大于0时,
w
w
w的为过大, 我们需要减小
w
w
w的值, 而当导数小于0时,
w
w
w的为过小, 我们需要增大
w
w
w的值, 所以我们调节w的值时只要减去求出来的导数就可以了.























 2704
2704

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








