本文是一位新手程序员的学习心得，主要涉及C++和数据结构的知识，包括指针的理解、链表、循环队列、二叉树的遍历、快速排序算法以及递归的概念。文章通过实例和代码解释了指针的用法，强调了初始化指针的重要性，并介绍了二叉树的先序、中序、后序遍历。此外，还探讨了递归的原理和在解决汉诺塔问题中的应用。
（声明：本人新手并且编程技术辣鸡，博客单纯记录自己成长和做笔记）
本科c语言学过一次，c++学过一次，研究生又学了一次c++，又学一次感觉还是一知半解的，如今学了《【郝斌】-数据结构入门 5_预备知识_指针_2_哔哩哔哩_bilibili》数据结构感觉自己才算是勉强理解了指针。
链表、循环队列、汉诺塔、二叉树、快排需要复习再敲一次代码；二叉树 先序遍历、中序遍历、后序遍历。
先把逻辑捋顺和把伪代码写出来。
学习讲究一个温故知新、后知后觉、熟能生巧，一定要保持不断学习，并且不断回顾总结。
越是困难的问题，克服后成就感越强！
（p5） 笔记1：
#include <stdio.h>
int main()
{
int * p;//p是变量名，int * 表示p变量只能储存int型的地址
int i=0;
int j;
test00
//p = &i;// *p=i ,p储存i的地址。p不是i，i也不是p，改变i/p的值，不改变p/i的值;p指向i，改变*p也改变ir
//*p = i;//p=i 重复赋值
//test01
p = &i;// *p=i ,p储存i的地址。p不是i，i也不是p，改变i/p的值，不改变p/i的值;p指向i，改变*p也改变i
j = *p;//理论上j=i,若没有上一行，这报错，因为p并没有保持int的地址，p保存的值随机不确定，c语言不允许这种不确定的情况（指向无效地址野指针？）
/*在C/C++语言中，一个指针变量如果没有被初始化，其值就是未定义的，它可能指向任何地址。当这个未初始化的指针被用来访问内存时，就会产生野指针。
野指针对程序的影响是不可预测的。当程序使用野指针时，可能会出现崩溃、数据损坏、内存泄漏等问题，这些问题都可能导致程序的运行失败。此外，由于野指针是不可预测的，因此调试野指针问题通常也比较困难，需要花费大量的时间和精力来定位和修复问题。
为避免野指针的问题，应该始终初始化指针变量，并在使用指针变量之前检查它们是否为NULL或有效的地址。同时，释放指针指向的内存空间后，应将指针赋值为NULL，以避免产生悬挂指针。*/
printf("i = %d, j = %d,*p = %d\n ",i,j,*p);
getchar();
//int i = 10;
//int* p = &i; //等价于int *p; p = &i;
return 0;
}笔记2：
#include <stdio.h>
int test(int * p)//定义了一个int * 型的形参变量p； 并不是定义了一个形参*p； int * 存放整型变量地址
{
*p = 100;// * p = i
}
int main()
{
//调用函数修改i的值
int i = 9;
test(&i);
printf("i= %d",i);
return 0;
}总结：感觉之前没理解主要原因是，定义时：“
int * p; //p是变量名，int * 表示p变量只能储存int型的地址使用时：用的 * p和定义的时候的 * p以为是一回事，实际上：定义int *p其真正含义应该是：p是变量名，int * 表示p变量只能储存int型的地址。
p = &i;// *p=i ,p储存i的地址。p不是i，i也不是p，改变i/p的值，不改变p/i的值;p指向i，改变*p也改变i
（p5）array_point_1,笔记:
a[i] == *(a+i)
a[3] == *(a+3)
a是数组首地址，那么*a就是数组首地址内容1，*a +3=1+3=4
array_point_2，笔记:
#include<stdio.h>
void show_array(int * p)
{
printf("a[i]=p[i],其中p[3]=%d\n",p[3]);
for (int i = 0; i < 5; i++)
{
printf("%d", p[i]);
}
/*
p[2] = -1; p[0] == *p
p[2] == *(p+2) == *(a+2) == a[2]
p[i]就是主函数的a[i]
*/
}
int main()
{
int a[5] = { 1,2,3,4,5 };
a等价于&a[0],&a[0]本身就是int * 类型
show_array(a);
}（p6）笔记：
6_所有的指针变量只占4个子节 用第一个字节的地址表示整个变量的地址_哔哩哔哩_bilibili
指针变量只占用4个字节（32位下），和它指向的变量所占字节多少无关。
（p7）笔记：
传入其地址
#include<stdio.h>
void fun(int * *p);
int main()
{
int i = 100;
int* p = i; //等价于int *p; p = &i;
fun(&p);//现在要改变指针变量p的地址
printf("%p",p);
}
void fun(int* * p)//p是int *型，然后传入p的地址也就是要 *
{
*p = (int*)0000;
}p8笔记
#include<stdio.h>
#include<string.h>
struct Student
{
int s_id;
char s_name[200];
int age;
};
int main()
{
struct Student st = {10,"张三",18};
printf("%d %s %d \n", st.s_id,st.s_name,st.age);
}
p24链表
可以参考：【头指针，头结点、首元节点】_x-inda的博客-优快云博客
主要：新节点插入的代码实现
这里有个地方要注意，就是对头指针概念的理解，这个很重要。“链表中第一个结点的存储位置叫做头指针”，如果链表有头结点，那么头指针就是指向头结点数据域的指针：
单链表也可以没有头结点。如果没有头结点的话：
#include<stdio.h>
#include<stdlib.h>
#include <cstring>
typedef struct node {
char data;
node* next;
}*LinkList, * pNode;
int len; //该变量用于存放字符串长度 即链表长度
int DIYstrlen(char* p) { //获取字符串长度
int n = 0;
while (*p++)
n++;
return n;
}
LinkList GetEmptyList() {
//初始化链表
//malloc时动态内存分配函数，用于申请一块连续的指定大小的内存块区域以void*类型返回分配的内存区域地址
LinkList head = (pNode)malloc(sizeof(pNode));
head->data = 0;
head->next = NULL;
return head;
}
//字符串到链表
LinkList String2LinkList(char str[]) {
LinkList L = GetEmptyList();
len = DIYstrlen(str);
//printf("字符串长度为：%d\n",len);
int i = 0;
pNode p = L;
while (str[i]) {
p->next = (pNode)malloc(sizeof(pNode));
p->next->data = str[i++];
p = p->next;
}
p->next = NULL;
return L;
}
//显示链表内容
void show(LinkList L) {
pNode p = L->next;
while (p) {
printf("%c ", p->data);
p = p->next;
}
printf("\n");
}
int main() {
char s[100];
printf("输入字符串：\n");
gets_s(s);
printf("链表的内容为：\n");
LinkList L = String2LinkList(s);
show(L);
return 0;
}
循环链表（数组实现）
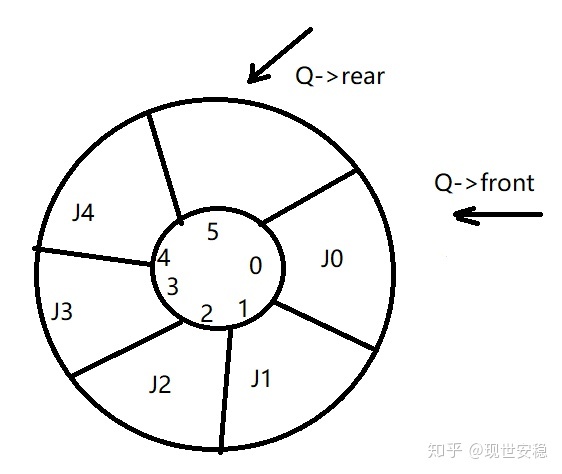
# include <stdio.h>
#include<stdlib.h>
struct Queue
{
int* p_Base;
int front;
int rear;
};
void init(Queue*);
bool insert(Queue*,int);
bool is_full(Queue*);
void traverse(Queue*);
bool is_empty(Queue*);
bool delete_queue(Queue*, int*);
int main()
{
Queue queue;
int val;
init(&queue);
insert(&queue,1);
insert(&queue, 2);
insert(&queue, 3);
insert(&queue, 4);
insert(&queue, 5);
insert(&queue, 6);
traverse(&queue);
if (delete_queue(&queue, &val))
{
printf("出队成功，队列出队的元素是: %d\n", val);
}
else
{
printf("出队失败!\n");
}
traverse(&queue);
}
void init(Queue* queue)
{
queue->p_Base = (int*)malloc(sizeof(int)*6);
queue->front = 0;
queue->rear = 0;
};
bool is_full(Queue* queue)
{
if ((queue->rear + 1) % 6== queue->front )
{
return true;
}
else
{
return false;
}
};
bool insert(Queue* queue, int num)
{
if (is_full(queue))
{
return false;
}
else
{
queue->p_Base[queue->rear] = num;
queue->rear = (queue->rear + 1) % 6;
return true;
}
};
bool is_empty(Queue* queue)
{
if (queue->front == queue->rear)
{
return true;
}
else
{
return false;
}
};
void traverse(Queue* queue)
{
if (is_empty(queue))
{
return ;
}
else
//易错
{
int i = queue->front;
while (i!=queue->rear)
{
printf("%d\n", queue->p_Base[i]);
i = (i + 1) % 6;
}
}
};
bool delete_queue(Queue* queue, int* val)
{
if (is_empty(queue))
{
return false;
}
else
{
*val = queue->p_Base[queue->front];
queue->front = (queue->front + 1) % 6;//易错
return true;
}
};
p50递归
知识点一：函数的调用
-
-
-
- 当在一个函数的运行期间调用另一个函数时，在运行被调函数之前，系统需要完成三件事：
- 将所有的实际参数，返回地址等信息传递给被调函数。
- 为被调函数的局部变量（也包括形参）分配存储空间
- 将控制转移到被调函数的入口
- 从被调函数返回主调函数之前，系统也要完成三件事：
- 保存被调函数的返回结果
- 释放被调函数所占的存储空间
- 依照被调函数保存的返回地址将控制转移到调用函数
- 当有多个函数相互调用时，按照“后调用先返回”的原则，上述函数之间信息传递和控制转移必须借助“栈”来实现，即系统将整个程序 运行时所需的数据空间安排在一个栈中，每当调用一个函数时，将在栈顶分配一个存储区，进行压栈操作，每当一个函数退出时，就释放它的存储区，就进行出栈操作，当前运行的函数永远都在栈顶位置。
- A函数调用A函数和A函数调用B函数在计算机看来是没有任何区别的，只不过用我们日常的思维方式比较怪异而已。
- 当在一个函数的运行期间调用另一个函数时，在运行被调函数之前，系统需要完成三件事：
-
-
知识点二：递归必须满足的三个条件
-
-
-
- 递归必须得有一个明确的终止条件
- 该函数所处理的数据规模必须在递减
- 这个转化必须是可解的
-
-
知识点三：递归和循环的优缺点比较
-
-
-
- 递归：
-
-
易于理解（编写：树、汉诺塔等情况下）
速度慢
存储空间大
-
-
-
- 循环
-
-
不易理解
速度快
存储空间小
知识点四：递归的应用
-
-
-
- 树和森林就是以递归的方式定义的
- 树和图的很多算法都是以递归来实现的
- 很多数学公式就是以递归的方式定义的
-
-
斐波拉契序列：1 2 3 5 8 13 21 34
汉诺塔：
#include<stdio.h>
/*
A柱子 B柱子 C柱子
1盘子：
1:A->C
2盘子：
1:A->B 2:A->C 1:B->C
3盘子:
1:A->C 2:A->B 1:C->B
3:A->C
1:B->A 2:B->C 1:A->C
伪代码：
如果一个盘子直接A移到C
如果是n个盘子
先将A的前n-1个盘子借助C移到B
将n号盘子直接A移到C
先将B的前n-1盘子借助A移到C
*/
void Tower_of_Hanoi(int ,char , char, char);
int main()
{
int n;
printf("输入盘子个数n:");
scanf_s("%d",&n);
Tower_of_Hanoi(n,'A','B','C');//哈诺塔,函数功能将n个盘子从A借助B移到C
}
void Tower_of_Hanoi(int n, char A, char B, char C)
{
if (n==1)
{
printf("将%d号盘子从%c移到%c\n", n, A, C);
}
else
{
Tower_of_Hanoi(n-1,A,C,B);
printf("将%d号盘子从%c移到%c\n", n,A,C);
Tower_of_Hanoi(n - 1, B, A, C);
}
};
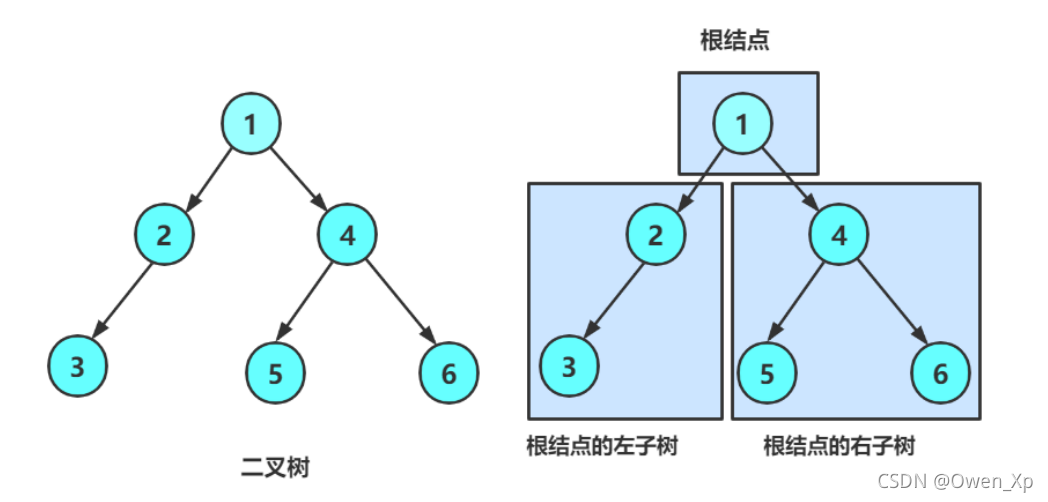
二叉树
#include<stdio.h>
#include<stdlib.h>
struct binary_tree
{
//binary_tree* p_root_node;不需要每个二叉树创立一个根节点，创立一个根节点，然后向下指向就行了
binary_tree* p_left_node;
binary_tree* p_right_node;
char data;
};
void create_binary_tree(binary_tree**);
void traverse_binary_tree(binary_tree*);
int main()
{
binary_tree* p_root_node=NULL;//创立第一个根节点
create_binary_tree(&p_root_node);
traverse_binary_tree(p_root_node);//函数功能：遍历二叉树;递归调用
}
void create_binary_tree(binary_tree** p_root_node)
{
/*上次错在此处
*
在定义二叉树结构体时，指针类型应该为 struct binary_tree*，而不是 binary_tree*。
在 create_binary_tree() 函数中，你需要动态分配内存来创建左右子树节点，否则会访问空指针，导致程序崩溃。
在 create_binary_tree() 函数中，你需要将左右子树节点指针初始化为 NULL，否则它们的初始值是不确定的，可能是一个随机值，会导致程序出错。
在 create_binary_tree() 函数中，你需要修改节点数据的赋值方式，正确的方式是 p_node->data = 'A';。
*/
//p_root_node->data = 'A';
//p_root_node->p_left_node->data = 'B';
//p_root_node->p_left_node->p_right_node = NULL;
//p_root_node->p_left_node->p_left_node->data = 'C';
//p_root_node->p_left_node->p_left_node->p_left_node = NULL;
//p_root_node->p_left_node->p_left_node->p_right_node = NULL;
//p_root_node->p_right_node->data = 'D';
//p_root_node->p_right_node->p_left_node->data = 'E';
//p_root_node->p_right_node->p_left_node->p_left_node = NULL;
//p_root_node->p_right_node->p_left_node->p_right_node = NULL;
//p_root_node->p_right_node->p_right_node->data = 'F';
//p_root_node->p_right_node->p_right_node->p_left_node = NULL;
//p_root_node->p_right_node->p_right_node->p_right_node = NULL;
//优化，先创立全部节点,后数据域赋值，然后将左右子树连起来
binary_tree* pA= (binary_tree*)malloc(sizeof(binary_tree));
binary_tree* pB = (binary_tree*)malloc(sizeof(binary_tree));
binary_tree* pC = (binary_tree*)malloc(sizeof(binary_tree));
binary_tree* pD = (binary_tree*)malloc(sizeof(binary_tree));
binary_tree* pE =(binary_tree*)malloc(sizeof(binary_tree));
binary_tree* pF = (binary_tree*)malloc(sizeof(binary_tree));
pA->data = 'A';
pB->data = 'B';
pC->data = 'C';
pD->data = 'D';
pE->data = 'E';
pF->data = 'F';
pA->p_left_node = pB;
pB->p_left_node = pC;
pB->p_right_node = NULL;
pC->p_left_node = NULL;
pC->p_right_node = NULL;
pA->p_right_node = pD;
pD->p_left_node = pE;
pD->p_right_node = pF;
pE->p_left_node = NULL;
pE->p_right_node = NULL;
pF->p_left_node = NULL;
pF->p_right_node = NULL;
/*
另外，在 create_binary_tree 函数中，你传递了一个指向根节点的指针 p_root_node，
但是你没有修改指针本身，而是在它指向的内存位置上修改了值。
这意味着在函数返回后，原始的指针仍然是空的。
为了在函数中修改指针本身，你应该传递一个指向指针的指针，例如：*/
*p_root_node = pA;
};
//自己调整先序、中序、后序
void traverse_binary_tree(binary_tree* p_root_node)
{
//先序
/*在 traverse_binary_tree() 函数中，你使用了% d 格式符输出字符数据，应该使用% c 格式符。*/
//printf("%d ", p_root_node->data);//节点
//
//递归要写限制条件！
if (p_root_node == NULL)
{
return;
}
printf("%c ", p_root_node->data);//节点
traverse_binary_tree(p_root_node->p_left_node);//先序遍历左子树
traverse_binary_tree(p_root_node->p_right_node);//先序遍历右子树
};
p76 快排
核心：递归，快速排序在每一轮挑选一个基准元素，并让其他比它大的元素移动到数列一边，比它小的元素移动到数列的另一边，从而把数列拆解成了两个部分
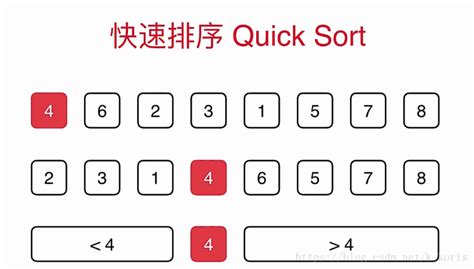
# include <stdio.h>
int FindPos(int* a, int low, int high);
void QuickSort(int* a, int low, int high);
int main(void)
{
int a[6] = { 2, 1, 5, -985, 2, -2 };
int i;
QuickSort(a,0,5);//将数组a,从a[0]到a[5]进行快速排序
for (i = 0; i < 6; ++i)
printf("%d ", a[i]);
printf("\n");
return 0;
}
int FindPos(int* a, int low, int high)
{
/*
将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
*/
int val = a[low];//不能用a[0],因为传入的low，也就是第一个下标是不同的。递归别用固定的值赋值或者输出，因为递归调参数会不断变化
while (low < high)//确保返回时low=high
{
while (low < high && a[high] >= val)//while( low < high:防止数组位置溢出 && >= :判断移位条件，与确保数组有相同数时排序唯一性 )
{
--high;
}
a[low] = a[high];
while (low < high && a[low] <= val)//while(low < high:防止数组位置溢出 && >= :判断移位条件，与确保数组有相同数时排序唯一性 )
{
++low;
}
a[high] = a[low];
}
//相等时别忘了赋值
a[low] = val;
return low;
}
void QuickSort(int* a, int low, int high)
{
/*
a. 先从数列中取出一个数作为基准数。
b. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
c. 再对左右区间重复第二步，直到各区间只有一个数。
*/
//递归别用固定的值赋值或者输出，因为递归调参数会不断变化 如下的
/*
pos = FindPos(a, 0, 5);//找出a[low]的位置
QuickSort(a, 0, pos - 1);
QuickSort(a, pos + 1, 5);
*/
int pos;
if (low < high)//限制条件数组元素只有一个时不用排序
{
pos = FindPos(a, low, high);//找出a[low]的位置
QuickSort(a, low, pos - 1);
QuickSort(a, pos + 1, high);
}
}先序后序中序
- 二叉树的遍历：
- 先序遍历【先访问根节点】
方法：(1)先访问根节点
(2)再先序访问左子树
(3)再先序访问右子树
中序遍历【中间访问根节点】
方法：(1)中序遍历左子树
(2)再访问根节点
(3)再中序遍历右子树
后序遍历【最后访问根节点】
方法：(1)先中序遍历左子树
(2)在中序遍历右子树
(3)再访问根节点
扫一扫
763
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
