异常检测——线性模型

1、引言

  真实数据集中不同维度的数据通常具有高度的相关性，这是因为不同的属性往往是由相同的基础过程以密切相关的方式产生的。在古典统计学中，这被称为——回归建模，一种参数化的相关性分析。
  一类相关性分析试图通过其他变量预测单独的属性值，另一类方法用一些潜在变量来代表整个数据。前者的代表是 线性回归，后者一个典型的例子是 主成分分析。本文将会用这两种典型的线性相关分析方法进行异常检测。

  需要明确的是，这里有两个重要的假设：

  假设一：近似线性相关假设。线性相关假设是使用两种模型进行异常检测的重要理论基础。

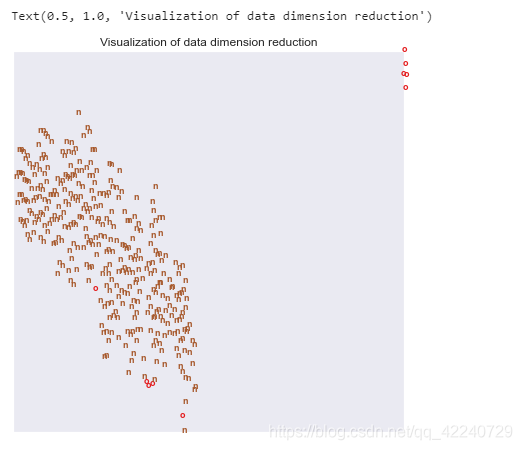
  假设二：子空间假设。子空间假设认为数据是镶嵌在低维子空间中的，线性方法的目的是找到合适的低维子空间使得异常点(o)在其中区别于正常点(n)。

  基于这两点假设，在异常检测的第一阶段，为了确定特定的模型是否适合特定的数据集，对数据进行探索性和可视化分析是非常关键的。

2、数据可视化

  以breast-cancer-unsupervised-ad数据集为例做一些简单的数据可视化。

#coding:utf-8
#导入warnings包，利用过滤器来实现忽略警告语句。
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import missingno as msno

## 1) 载入训练集和测试集；
path = 'dataverse_files/'
f=open(path+'breast-cancer-unsupervised-ad.csv')
Train_data = pd.read_csv(f)

## 2) 简略观察数据(head()+shape)
Train_data.head()

## 2) 简略观察数据(tail()+shape)
Train_data.tail()

## 1) 通过describe()来熟悉数据的相关统计量
Train_data.describe()

## 2) 通过info()来熟悉数据类型
Train_data.info()

numeric_features = ['f' + str(i) for i in range(30)]

## 1) 相关性分析
numeric = Train_data[numeric_features]
correlation = numeric.corr()

f , ax = plt.subplots(figsize = (14, 14))

sns.heatmap(correlation,square = True)
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
plt.show())

## 3) 每个数字特征得分布可视化
f = pd.melt(Train_data, value_vars=numeric_features)
g = sns.FacetGrid(f, col="variable",  col_wrap=6, sharex=False, sharey=False)
g = g.map(sns.distplot, "value", hist=False, rug=True)

#变量两两之间的相关性
sns.set()
sns.pairplot(Train_data[numeric_features],size = 2 ,kind ='scatter',diag_kind='kde')
plt.savefig('correlation.png')
plt.show()

部分展示

#数据降维可视化
from sklearn.manifold import TSNE
tsne = TSNE(n_components=2, init='pca', random_state=0)
result = tsne.fit_transform(numeric)
x_min, x_max = np.min(result, 0), np.max(result, 0)
result = (result - x_min) / (x_max - x_min)
label = Train_data['label']
fig = plt.figure(figsize = (7, 7))
#f , ax = plt.subplots()
color = {
   'o':0, 'n':7}
for i in range(result.shape[0]):
    plt.text(result[i, 0], result[i, 1], str(label[i]),
                color=plt.cm.Set1(color[label[i]] / 10.),
                fontdict={
   'weight': 'bold', 'size': 9})
plt.xticks([])
plt.yticks([])
plt.title('Visualization of data dimension reduction')

3、线性回归

  在线性回归中，我们假设不同维度的变量具有一定的相关性，并可以通过一个相关系数矩阵进行衡量。因此对于特定的观测值，可以通过线性方程组来建模。在实际应用中，观测值的数量往往远大于数据的维度，导致线性方程组是一个超定方程，不能直接求解。因此需要通过优化的方法，最小化模型预测值与真实数据点的误差。

  线性回归是统计学中一个重要的应用，这个重要的应用往往是指通过一系列自变量去预测一个特殊因变量的值。在这种情况下，异常值是根据其他自变量对因变量的影响来定义的，而自变量之间相互关系中的异常则不那么重要。这里的异常点检测主要用于数据降噪，避免异常点的出现对模型性能的影响，因而这里关注的兴趣点主要是正常值(n)。

  而我们通常所说的异常检测中并不会对任何变量给与特殊对待，异常值的定义是基于基础数据点的整体分布，这里我们关注的兴趣点主要是异常值(o)。

广义的回归建模只是一种工具，这种工具既可以用来进行数据降噪也可以进行异常点检测。

3.1 基于自变量与因变量的线性回归

3.1.1 最小二乘法

  为了简单起见，这里我们一元线性回归为例:

$$Y=\sum _{i=1}^d{a}_i\cdot X_i+a_{d+1}$$

  变量Y为因变量，也就是我们要预测的值；$X_1...X_d$为一系列因变量，也就是输入值。系数$a_1...a_{d+1}$为要学习的参数。假设数据共包含$N$个样本，第$j$个样本包含的数据为$x_{j1}...x_{jd}$和$y_j$，带入式(1)如下式所示：

y j = ∑ i = 1 d a i ⋅ x j i + a d + 1 + ϵ j y_{j}=\sum_{i=1}^{d} a_{i} \cdot x_{j i}+a_{d+1}+\epsilon_{j} yj​=i=1∑d​ai​⋅x