结构光三维重建（四步相移&多频外差法）matlab实现（一）

前言：这里主要梳理自己在理解四步相移法和三频外差法，以及用MATLAB实现条纹图生成，四步相移求相位主值，三频外差相位展开（解包裹）的过程。
废话不多说，一些基本思想概念可以看下面参考文章，里面有详细介绍。这里主要对遇到的问题展开阐述。

多频外差法

由于用周期性变化的黑白条纹编码整幅图像，导致通过相移法获得的相位主值包裹在[-pi,pi]之间，相位不具备唯一性，此时就涉及相位展开，即解包裹的问题。

1. 通过四步相移法：
   

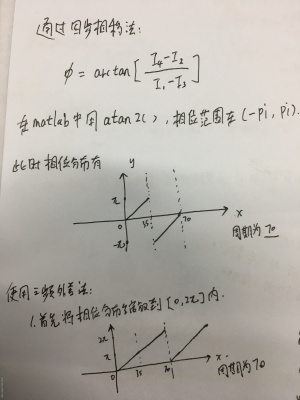
2. 选择三种光栅频率：
   这里参考李中伟博士的博士论文中提到的三种光栅频率。
   

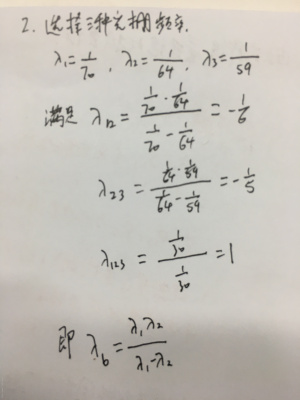
3. 进行相位差值运算：
   此节参考文章：https://blog.youkuaiyun.com/weixin_43263382/article/details/123090465
   
   故：经过公式验证知，两高频率光栅转化为低频率光栅时，相位值等于两频率相位作差。

4. 相位展开：
   此节参考文章：https://blog.youkuaiyun.com/weixin_43263382/article/details/123090465
   因为T123已经可以覆盖整幅图像所以其中的相位可以认为为绝对相位。下面就是对某一包裹相位进行展开一般最后选择频率最高的进行相位展开，这是因为高频的信噪比比较高，误差较小。
   详细计算公式推导过程如下：
   
   其中由图中，根据平行原理，可以知道，包裹区域相位值是以2nπ的量值增长。根据公式即可展开绝对相位。

5. 问题展开：
   理论理解内容基本就到此结束，在matlab实现过程中，遇到了三个问题：
   注：问题发现主要是在代码实现过程中遇到的，后面会给出代码，结合代码的话，容易理解。（代码链接在最下面）

6. 问题解答：
问题一：λ 12，λ 23，λ 123中的频率代表含义，以及与其图像，像素点值有什么关系？
通过在解决这一问题途中，发现自己原来的条纹图生成周期有问题。比如一幅宽为1110的图像，其正弦条纹频率，宽度为70。
我原文生成的是：每个像素点值以1/70递进；即70为正弦条纹的周期。
但实际上是：正弦条纹频率70，即代表整幅图像出现的正弦条纹条数为70；正弦条纹宽度即有1110/70;
帮助理解的参考文章：https://blog.youkuaiyun.com/qq_33810188/article/details/89921099
如此一来，对于整幅图：
λ 12的频率为1/6即代表整幅图有6条正弦条纹。
λ 23的频率为1/5即代表整幅图有5条正弦条纹。
λ 123的频率为1即代表整幅图有1条正弦条纹。

问题二：作相位差时，θ12，θ23，θ123为什么也要缩放到[0,2pi]？
%将截断相位映射到0~2π
phaseMap(phaseMap<0)=phaseMap(phaseMap<0)+2*pi;

类似这行代码，在代码中，有两处地方出现。
第一次是在经过四步相移法后，由于atan2()函数，原本是0~2pi的相位值，被分成了两部分，因而需要还原。如图，不仅是因为要使用三频外差，才缩放到[0,2pi]；而是因为，本来的相位值就是[0,2pi]递增的。

第二次则是在相位作差的时候，可以看到，叠加频率的相位值范围也应该是[0,2pi]递增的。

单纯经过相减后，可以发现有正值也有负值；而在实际运算中，为什么通过代码：
phaseMap(phaseMap<0)=phaseMap(phaseMap<0)+2*pi;
，即将负值加2pi就能还原到正确值？是我的疑惑点； 之后，通过debug，推了一遍数据值演算结果，找到了答案。

问题三：既然θ123是频率为1的绝对相位，为什么不直接作为含有物体信息的相位值使用，还要对θ1或θ2或θ3进行绝对相位展开？
通过查看θ123的数值分布发现，相位值都是在[0,2pi]之内；虽然θ123为绝对相位，但与其要展开的，折叠多个2pi的绝对相位数值分布不同。同时，考虑到对于有物体的条纹图，如果进行多个不同频率相位相减，越是多个频率交错相减，作差次数越多，其结果越混乱，尽管最后能整合为频率为1的绝对相位，但对于物体相位，不具有代表性或实际意义。考虑到这一点，也就觉得θ123是不合适的了。

参考文章：
https://zhuanlan.zhihu.com/p/432343200
https://blog.youkuaiyun.com/weixin_43263382/article/details/123090465?spm=1001.2014.3001.5502
https://blog.youkuaiyun.com/weixin_43263382/article/details/123220055
https://blog.youkuaiyun.com/qq_33810188/article/details/89921099
https://blog.youkuaiyun.com/weixin_40204808/article/details/115376564
https://blog.youkuaiyun.com/qq_27353621/article/details/124235712
https://blog.youkuaiyun.com/qq_33810188/article/details/89921099

下章将附上完整MATLAB代码。
结构光三维重建（四步相移&多频外差法）matlab实现（二）