

- intuition about Gradient Descent: How the algorithm works & why the updating step makes sense
to know how the formula works, again we reduce the original problem to a simplified problem with only one parameter.
𝑎0≔𝑎0− 𝛼𝑑𝐽(𝑎0)𝑑𝑎0 (𝑗=0)
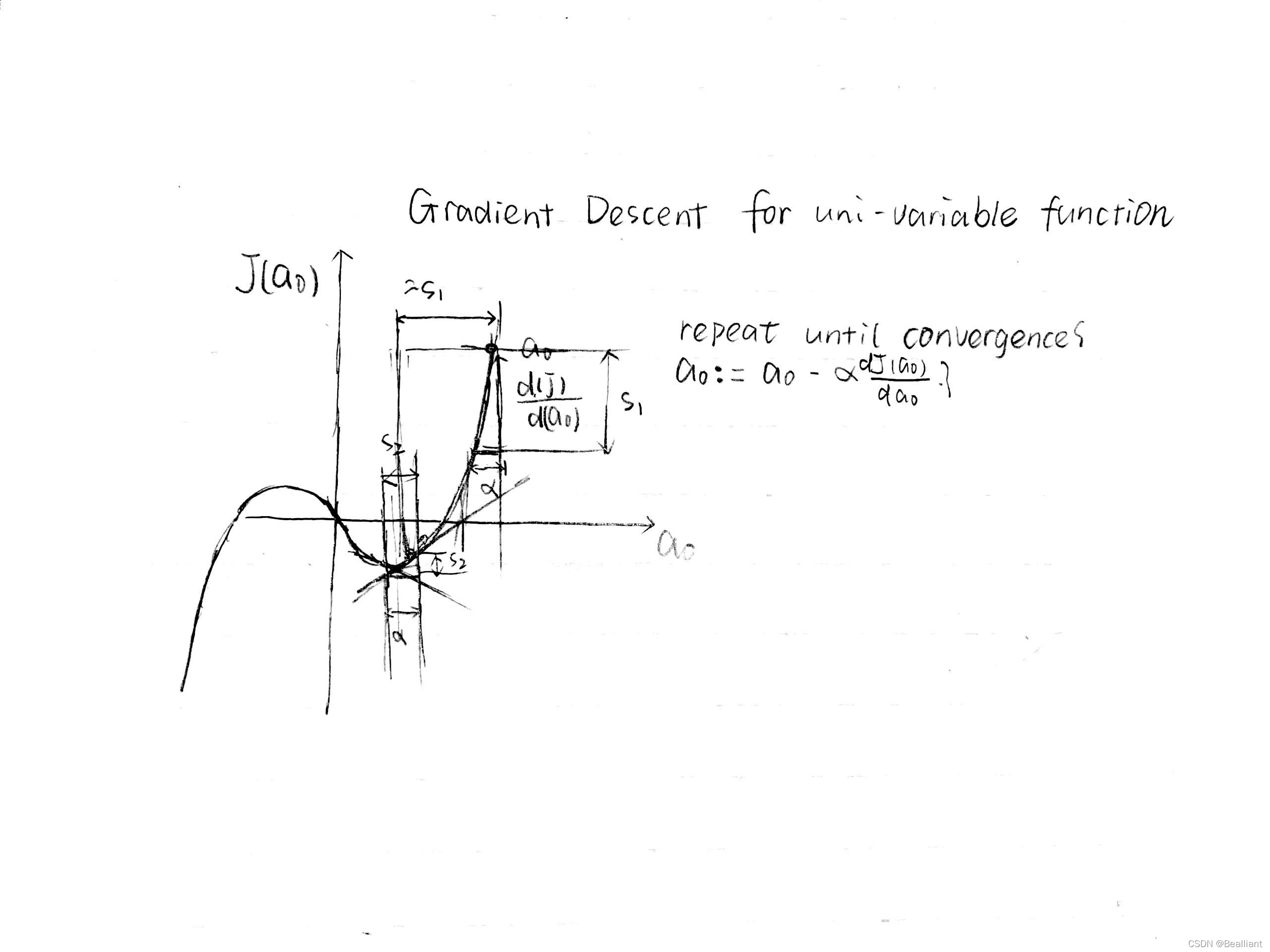
𝑑𝐽(𝑎0)𝑑𝑎0 means the partial derivative of one point, and has its geometrical meaning - the slope of the tangent to the point.
If alpha is too small, gradient descent may be low; while alpha is too large, it may overshoot the minimum, making it fail to converge, or may diverge.
If you have already reached the local optimum, the derivative term will be 0 so you won't take steps any more.
Remember the magnitude of the step you take is both related to the Learning Rate and the derivative value of the last point. So when you are stepping closer to the minimum point, you will automatically take smaller steps.
Finally, if we put the Cost Function and Gradient Descent together, we will accomplish the first Learning Algorithm - Linear Regression.
that is finally how we realized the algorithm.
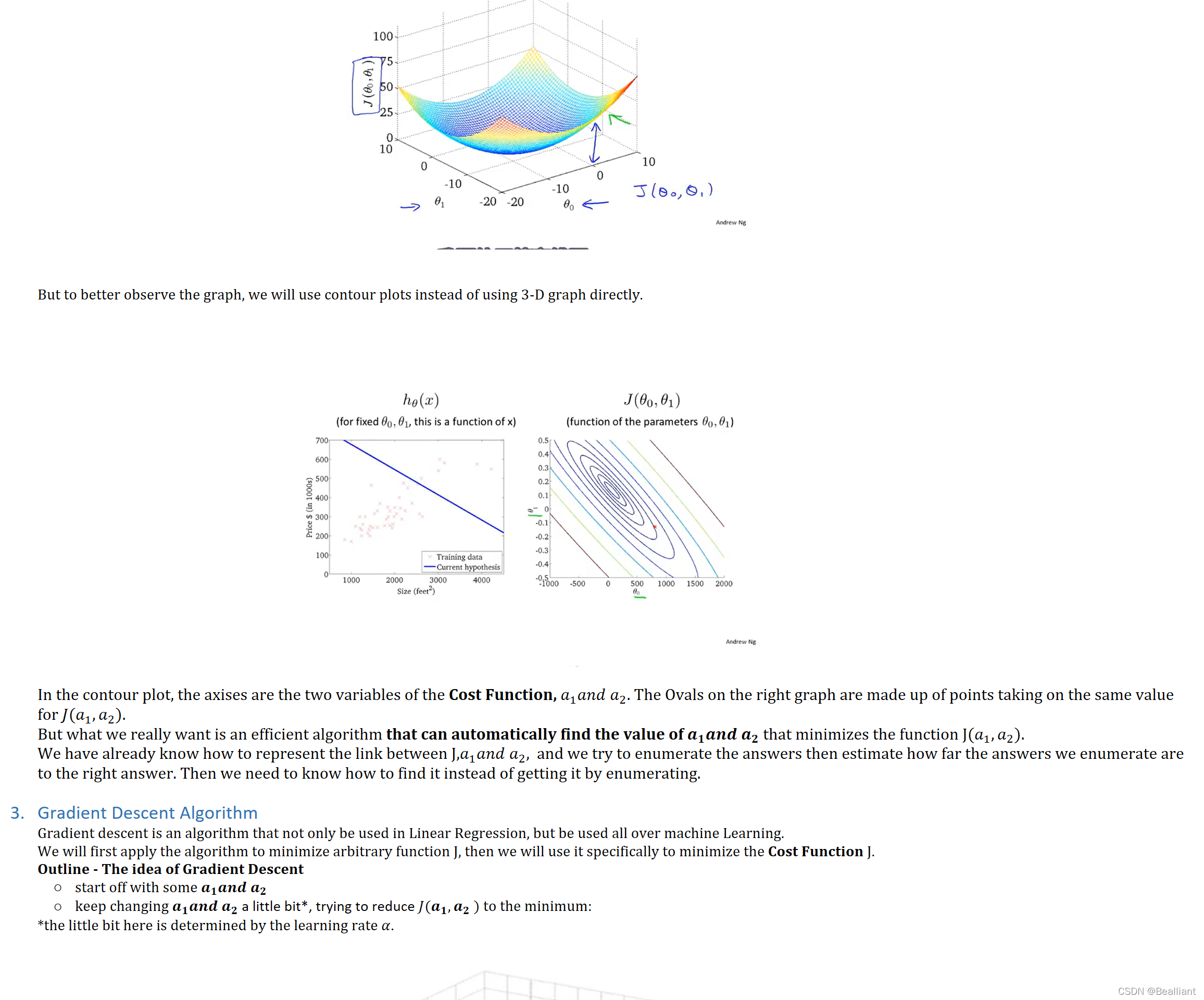
Now we look back to the original problem.
In a one-parameter function f(x_1), the graph of function f is just a 2-D curve. In a two-parameter function, however, the graph of the function is a 3-D curved surface with three axes - we call it axis x, axis y and axis z.

we assume that the coordinate of the point P is (𝑥0,𝑦0,𝑧0) and the vertical axis, z represents the value of the function J(x,y). So it's not too hard to understand the meaning of the partial derivative. The derivative to x is in the (x,𝑦0,z) surface, and the derivative to y is in the (𝑥0,𝑦,𝑧) surface. 
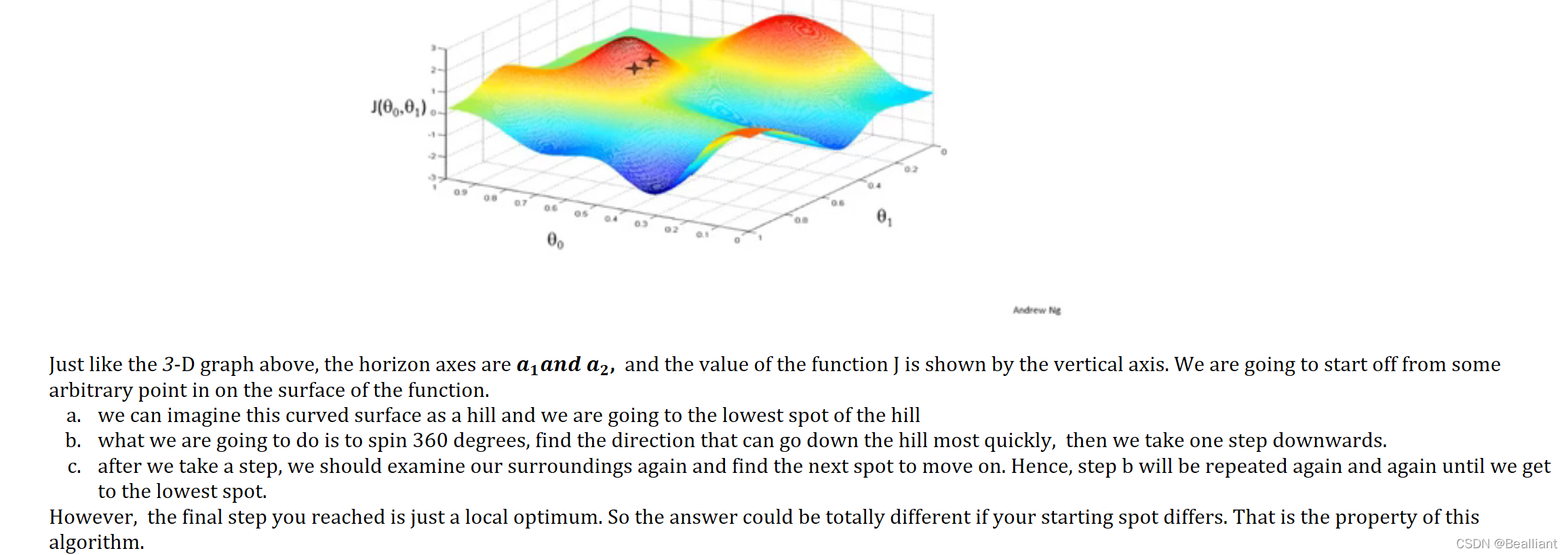
In this 3-D surface, you can imagine you are going down a real hill and should decide which direction to go.
The 𝒂𝟏𝒂𝒏𝒅 𝒂𝟐 should update every time so that you find the right point (𝒂𝟏 , 𝒂𝟐) in the horizontal surface corresponding to the minimum J.![]()
That's why 𝑎1𝑎𝑛𝑑 𝑎2 should update simultaneously instead of separately.![]()

So congrats on finishing the first Machine Learning Algorithm.
- double-parameter Linear Regression Realization








 本文深入浅出地介绍了梯度下降算法的基本原理及其在机器学习中的应用。通过简化问题到只有一个参数的情况来直观理解梯度下降如何工作及更新步骤背后的含义。文章还探讨了学习率的选择对算法收敛的影响,并最终实现了线性回归这一机器学习算法。
本文深入浅出地介绍了梯度下降算法的基本原理及其在机器学习中的应用。通过简化问题到只有一个参数的情况来直观理解梯度下降如何工作及更新步骤背后的含义。文章还探讨了学习率的选择对算法收敛的影响,并最终实现了线性回归这一机器学习算法。
















 3970
3970

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








