本文介绍了如何使用Python构建有限域，并展示了模运算的相关代码实现，包括加减乘除和幂运算。通过一系列练习，逐步探讨了有限域内的数值操作，并提供了单元测试用例进行验证。此外，还讨论了费马小定理在处理负指数时的应用。
文章目录
《区块链编程》
使用Python构建有限域
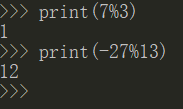
Python的模运算
p16
书中代码复现 ，。p13
代码复现
# -*- coding: utf-8 -*-
# @Author: 从化北(喵星人)
# @Date: 2021-11-26 22:15:25
# @Last Modified by: 从化北
# @Last Modified time: 2021-11-26 22:29:58
class FieldElement:
def __init__(self, num, prime):
# 有限域内值范围[0,prime -1]
if num >= prime or num < 0:
error = 'Num {} not in field range 0 to {}'.format(
num, prime - 1)
raise ValueError(error)
self.num = num
self.prime = prime
def __repr__(self):
# 文本格式化
return 'FieldElement_{}({})'.format(self.prime, self.num)
def __eq__(self, other):
# 重写== 符号
if other is None:
return False
return self.num == other.num and self.prime == other.prime
测试
练习1
p14
问题： 为FieldElement增加__ne__方法…
lzg：哭了，看到参考答案的那一刻，我感觉自己好菜呀。（是不理解问题本质的原因吗？）
自己写的
def __ne__(self, other):
# 重写 no equal
if other is None:
return False
print("this is ne ")
return self.num != other.num or self.prime != other.prime
参考答案
def __ne__(self, other):
# this should be the inverse of the == operator
# 调用了__eq__（）
return not (self == other)
测试
代码复现
练习2
p18
代码复现
练习3
p19
代码实现
def __sub__(self, other):
if self.prime != other.prime :
raise TypeError("Can't sub two numbers in diffrent Fields")
num = (self.num - other.num) % self.prime
return self.__class__(num, self.prime)
练习4
p20
代码实现
print((97 * 45 * 31) % 97)
print((17 * 13 * 19 * 44) % 97)
print((12**7 * 77**49) % 97)
运行结果
0
68
63
[Finished in 260ms]
练习5
p20
代码实现
prime = 19
k = [1, 7, 13, 18]
for x in k:
pass
print([x * y % prime for y in range(prime)])
print("this is sorted result:")
for x in k:
print(sorted([x * y % prime for y in range(prime)]))
运行结果
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
[0, 7, 14, 2, 9, 16, 4, 11, 18, 6, 13, 1, 8, 15, 3, 10, 17, 5, 12]
[0, 13, 7, 1, 14, 8, 2, 15, 9, 3, 16, 10, 4, 17, 11, 5, 18, 12, 6]
[0, 18, 17, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
this is sorted result:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18]
[Finished in 247ms]
练习6
p20
代码实现
def __mul__(self, other):
if self.prime != other.prime:
raise TypeError('Cannot mul two numbers in diffrent Fields')
num = (self.num * other.num) % self.prime
return self.__class__(num, self.prime)
运行结果
# a = FieldElement(24, 31)
# b = FieldElement(19, 31)
# print(a * b == FieldElement(22, 31))
True
[Finished in 299ms]
练习7
p21
代码实现
list_prime = [7, 11, 17, 31]
for prime in list_prime:
for x in range(1, prime):
# print(x, prime - 1, prime)
print(pow(x, prime - 1, prime), end=" ")
运行结果
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 [Finished in 298ms]
练习8
p23
代码实现
prime = 31
print(3 * pow(24, prime - 2, prime) % prime)
print(pow(17, prime - 4, prime))
print(11 * (pow(4, prime - 5, prime)) % prime)
运行结果
4
29
13
[Finished in 485ms]
练习9
p23
这部分要修改__pow__()函数，使其能处理负数次幂
原理是费马小定理，具体解释在书上p24
代码实现
def __pow__(self, exponent):
n = exponent
while n < 0:
n += self.prime - 1
num = pow(self.num, n, self.prime)
return self.__class__(num, self.prime)
def __truediv__(self, other):
if self.prime != other.prime:
raise TypeError('Cannot mul two numbers in diffrent Fields')
num = (self.num * pow(other.num, self.prime - 2, self.prime)) % self.prime
return self.__class__(num, self.prime)
模运算的计算公式
保留–等待写
三种取值方式
Java/C++ 与Python选择取值方式的不同
本章完整代码
# -*- coding: utf-8 -*-
# @Author: 从化北(喵星人)
# @Date: 2021-11-26 22:52:07
# @Last Modified by: 从化北
# @Last Modified time: 2021-12-06 18:20:17
import unittest
class FieldElement:
def __init__(self, num, prime):
# 有限域内值范围[0,prime -1]
if num >= prime or num < 0:
error = 'Num {} not in field range 0 to {}'.format(
num, prime - 1)
raise ValueError(error)
self.num = num
self.prime = prime
def __repr__(self):
# 文本格式化
return 'FieldElement_{}({})'.format(self.prime, self.num)
def __eq__(self, other):
# 重写== 符号
if other is None:
return False
# print("this is eq ")
return self.num == other.num and self.prime == other.prime
def __ne__(self, other):
# this should be the inverse of the == operator
return not (self == other)
# 重写 no equal
if other is None:
return False
print("this is ne ")
return self.num != other.num or self.prime != other.prime
return not (self == other)
def __add__(self, other):
if self.prime != other.prime:
raise TypeError('Cannot add two numbers in diffrent Fields')
num = (self.num + other.num) % self.prime
return self.__class__(num, self.prime)
def __sub__(self, other):
if self.prime != other.prime:
raise TypeError("Can't sub two numbers in diffrent Fields")
num = (self.num - other.num) % self.prime
return self.__class__(num, self.prime)
def __mul__(self, other):
if self.prime != other.prime:
raise TypeError('Cannot mul two numbers in diffrent Fields')
num = (self.num * other.num) % self.prime
return self.__class__(num, self.prime)
def __pow__(self, exponent):
n = exponent
while n < 0:
n += self.prime - 1
num = pow(self.num, n, self.prime)
return self.__class__(num, self.prime)
def __truediv__(self, other):
if self.prime != other.prime:
raise TypeError('Cannot mul two numbers in diffrent Fields')
num = (self.num * pow(other.num, self.prime - 2, self.prime)) % self.prime
return self.__class__(num, self.prime)
class FieldElementTest(unittest.TestCase):
def test_ne(self):
a = FieldElement(2, 31)
b = FieldElement(2, 31)
c = FieldElement(15, 31)
self.assertEqual(a, b)
self.assertTrue(a != c)
self.assertFalse(a != b)
def test_add(self):
a = FieldElement(2, 31)
b = FieldElement(15, 31)
self.assertEqual(a + b, FieldElement(17, 31))
a = FieldElement(17, 31)
b = FieldElement(21, 31)
self.assertEqual(a + b, FieldElement(7, 31))
def test_sub(self):
a = FieldElement(29, 31)
b = FieldElement(4, 31)
self.assertEqual(a - b, FieldElement(25, 31))
a = FieldElement(15, 31)
b = FieldElement(30, 31)
self.assertEqual(a - b, FieldElement(16, 31))
def test_mul(self):
a = FieldElement(24, 31)
b = FieldElement(19, 31)
self.assertEqual(a * b, FieldElement(22, 31))
def test_pow(self):
a = FieldElement(17, 31)
self.assertEqual(a**3, FieldElement(15, 31))
a = FieldElement(5, 31)
b = FieldElement(18, 31)
self.assertEqual(a**5 * b, FieldElement(16, 31))
def test_div(self):
a = FieldElement(3, 31)
b = FieldElement(24, 31)
self.assertEqual(a / b, FieldElement(4, 31))
a = FieldElement(17, 31)
self.assertEqual(a**-3, FieldElement(29, 31))
a = FieldElement(4, 31)
b = FieldElement(11, 31)
self.assertEqual(a**-4 * b, FieldElement(13, 31))
if __name__ == '__main__':
unittest.main()
# a = FieldElement(24, 31)
# b = FieldElement(19, 31)
# print(a * b == FieldElement(22, 31))
# prime = 31
# print(3 * pow(24, prime - 2, prime) % prime)
# print(pow(17, prime - 4, prime))
# print(11 * (pow(4, prime - 5, prime)) % prime)
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
