Dijkstra算法原理

一.特点

Dijkstra算法适合处理有权的图,从一点到其他所有点的最短路径
无优化的复杂度是O(n^2),如果需求所有点之间的最短路径,请使用 floyd
算法

---

二.思想

首先来一张图

求A与E的最短路径

1. 引入两个集合S,U(推荐使用数组),S包括已求出最短路径的点,U包括未求出最短路径的点
2. 将其与Ａ未直接链接的点设为极大值
3. 从U集合中找出路径最短的点，加入S集合,例如 A->Ｂ = 3
4. 更新U集合路径，if ( ‘此点 到 其他点的距离 + 起始点 到 此点的距离’ < '起始点 到 其他点 ’ ) 则更新U,例如 (B->C = 1) + (A->B = 3) = 4 < (A->C=5) 所U集合中A->C的距离更新到4
5. 重复3,4直到Ｕ集合空或找到目标点

三.详细分析

1. 选定初始点Ａ初始化
   S=[A->A=0]
   U=[A->B=3,A->C=5,A->F=MAX,A->D=MAX,A->E=MAX]
2. 选择U中最小的数值 如A->B=3加入S集合
   
   再循环计算B->C,B->F+A-B是否大于A->C,A->F,更新U集合
   S=[A->A=0,A->B=3]
   U=[A->F=6,A->C=4,A->D=MAX,A->E=MAX]
3. 重复上面动作直到E加入S集合
   
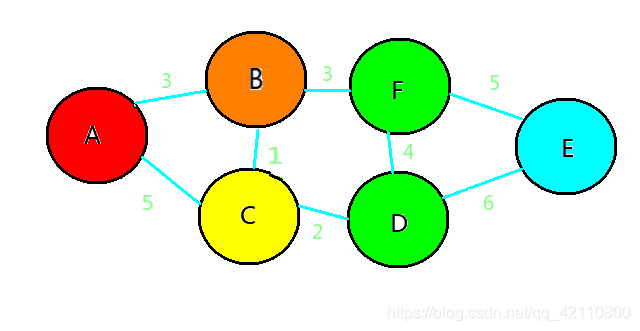
   红色:第1次加入S集合
   橙色:第2次加入S集合
   黄色:第3次加入S集合
   绿色:第4次加入S集合
   蓝色:第5次加入S集合

---

四.注意事项

如果有Ｕ集合中有距离相同就将他们一起加入,如上图出现了两个绿色是因为A->F=6,A->D=6所以计算两次,不影响结果