输入一个树状天平,根据力矩相等原则判断是否平衡。如图6-5所示,所谓力矩相等,就是W l D l =W r D r ,其中W l 和W r 分别为左右两边砝码的重量,D为距离。
采用递归(先序)方式输入:先输入样例个数,空行,每个天平的格式为W l ,D l ,W r ,D r ,当W l 或W r 为0时,表示该“砝码”实际是一个子天平,接下来会描述这个子天平。当W l =W r =0时,会先描述左子天平,然后是右子天平。
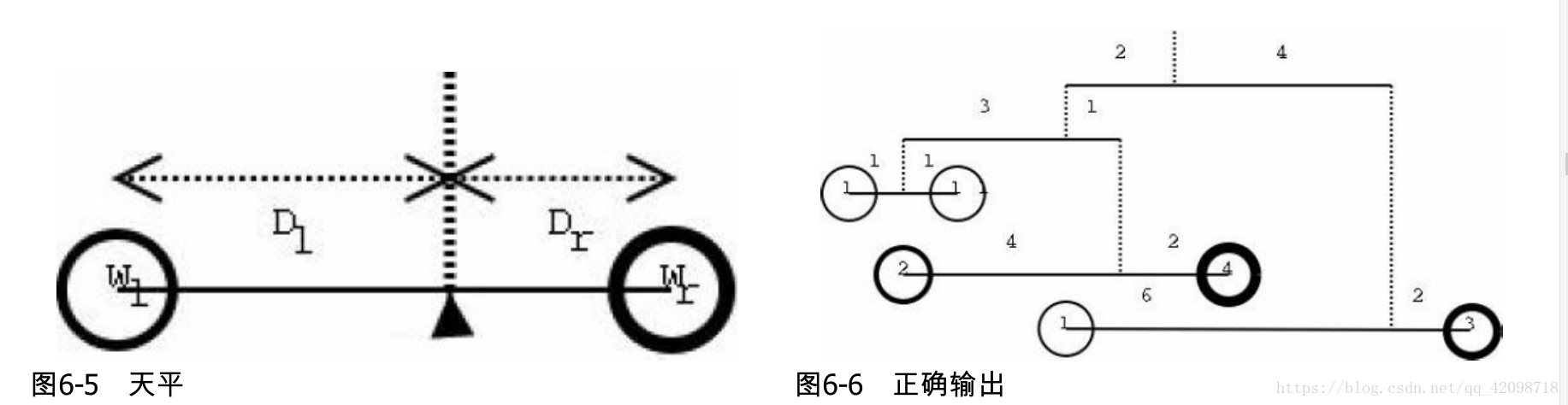
样例输入:
1
0 2 0 4
0 3 0 1
1 1 1 1
2 4 4 2
1 6 3 2
其正确输出为YES,对应图6-6。
分析:对于每个子树根节点来说,首先其左右子树分别都要平衡,最后左右子树的重量满足力矩平衡。很明显要用递归。
AC代码如下:
#include <bits/stdc++.h>
using namespace std;
#define fast ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define ll long long
#define _for(i,a,b) for(int i = a;i < b;i++)
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define all(s) s.begin(), s.end()
int kase;
bool solve(int& W)
{
int w1, d1, w2, d2;
scanf("%d%d%d%d", &w1, &d1, &w2, &d2);
bool b1 = true; bool b2 = true;
if (!w1) b1 = solve(w1);//判断左子树是否平衡
if (!w2) b2 = solve(w2);//判断右子树是否平衡
W = w1 + w2;//子树的总质量
return b1 && b2 && (w1*d1 == w2 * d2);
}
int main()
{
int W;//子天平的总重量
scanf("%d", &kase);
while (kase--)
{
if (solve(W))printf("YES\n"); else printf("NO\n");
if (kase)printf("\n");
}
return 0;
}





 本文介绍了一种使用递归算法来判断树状天平是否平衡的方法。通过力矩相等的原则(WlDl=WrDr),其中Wl和Wr为砝码重量,D为距离,实现了一个递归函数来解决这一问题,并给出了完整的代码实现。
本文介绍了一种使用递归算法来判断树状天平是否平衡的方法。通过力矩相等的原则(WlDl=WrDr),其中Wl和Wr为砝码重量,D为距离,实现了一个递归函数来解决这一问题,并给出了完整的代码实现。
















 483
483

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








