PriorityQueue的深入解析

PriorityQueue的深入解析

一：体系结构

二：PriorityQueue的概念

PriorityQueue是一个基于优先级的无界优先队列。(英文解析：Priority:优先级；Queue:队列)
通俗的讲：添加到PriorityQueue里面的元素都经过内部源码(下面讲)的排序(体现了其优先级)处理，默认按照自然排序法(从而实现的是最小堆)，也可以通过Comparator接口进行自定义排序(实现最小/大堆，根据你定义的排序规则而定)，后者自定义排序的方式有2种：
1. 添加元素自身实现了Comparable接口，确保元素是可以排序的对象；
2. 如果添加的元素没有实现Comparator接口，则可以在创建PriorityQueue对象时直接指定比较器；
PriorityQueue是一个无界队列，随着不断向其添加元素(该元素不能为null元素或者不可比较的对象元素)，当其元素个数大于等于其初始的容量(为11)时会自动扩容，无需指定容量增加策略的细节。
PriorityQueue是采用树形结构来描述元素的存储，具体说是通过完全二叉树实现一个最小/大堆，
在物理存储方面，PriorityQueue底层通过数组实现元素的存储。
图示：

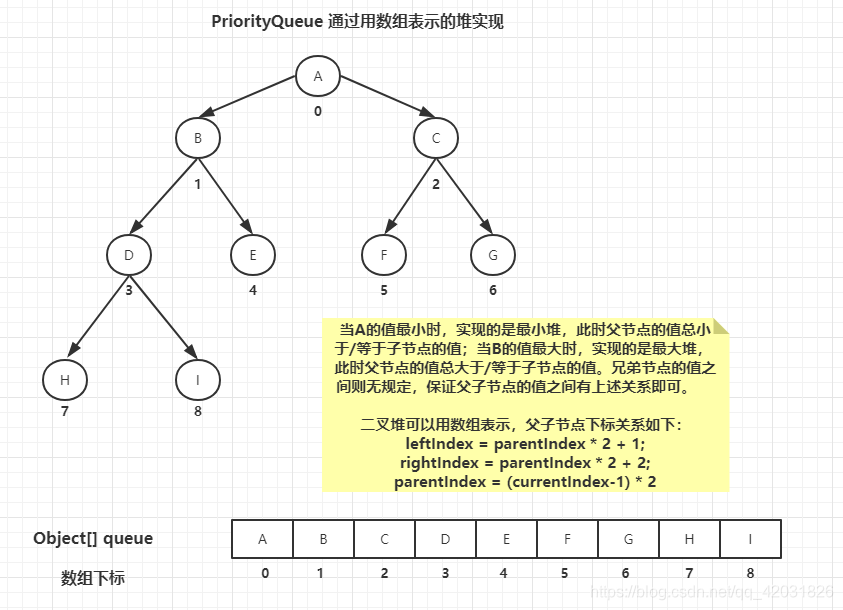
对上图说明：每个元素下面数字为其下标，上图中各参数含义：
parentIndex：父节点下标；
leftIndex：左子元素节点下标；
rightIndex：右子元素节点下标；
currentIndex：当前元素节点下标；
通过图中的三个公式，可计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储元素实现二叉树结构。

三：使用分析

自然排序：

	/**
	 * 自然排序
	 */
	public static void main(String[] args) {
		PriorityQueue<Integer> queue = new PriorityQueue<>();
		System.out.println("插入数据:");
		//随机添加两位数
		for(int i=0; i<10; i++) {
			Integer num = new Random().nextInt(90)+10;
			System.out.print(num+",");
			queue.offer(num);
		}
		System.out.println("\n插入后优先队列内的数据:");
		while(true) {
			Integer result = queue.poll();
			if(result==null){
				break;
			}
			System.out.print(result+",");
		}
	}

输出结果：

	插入数据:
	21,89,14,74,11,97,74,89,64,75,
	插入后优先队列内的数据:
	11,14,21,64,74,74,75,89,89,97,

自定义排序：

	/**
	 * 自定义排序
	 */
	public static void main(String[] args) {
		PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
			/**
			 * 重写compare方法。
			 * 在此体现了所谓的"自定义"：即根据自己所写逻辑来决定实现最大/小堆
			 */
			@Override
			public int compare(Integer o1, Integer o2) {
				//按从大到小排序，实现最大堆
				return o2-o1;
				//按从小到大排序，实现最小堆
				//return o1-o2;
			}
		});
		System.out.println("插入的数据:");
		//随机添加两位数
		for(int i=0; i<10; i++) {
			Integer num = new Random().nextInt(90)+10;
			System.out.print(num+",");
			queue.offer(num);
		}
		System.out.println("\n插入后优先队列内的数据:");
		while(true) {
			Integer result = queue.poll();
			if(result==null) {
				break;
			}
			System.out.print(result+",");
		}
	}

输出结果：

插入的数据:
18,12,62,18,44,26,65,37,18,87,
插入后优先队列内的数据:
87,65,62,44,37,26,18,18,18,12,

四：源码分析

4.1 以此示例代码为引子分析PriorityQueue源码

public static void main(String[] args) {
		//第一段
		PriorityQueue<Integer> queue = new PriorityQueue<Integer>(new Comparator<Integer({
			public int compare(Integer s1,Integer s2) {
				return(s1-s2);//实现最小堆
			}
		});
		//第二段
		queue.add(12);//将指定的元素插入此优先队列
		//第三段
		queue.poll();//取出元素
	}

4.2 第一段代码分析：

进入PriorityQueue.class，先看一下它的一些全局变量：

public class PriorityQueue<E> extends AbstractQueue<E>
    implements java.io.Serializable {
		private static final int DEFAULT_INITIAL_CAPACITY = 11;//默认初始化容量，默认11
		   
	    transient Object[] queue; //队列容器(存放Object类型元素的一维数组)

	    private int size = 0;//队列长度，即队列的元素个数，默认0

	    private final Comparator<? super E> comparator;//比较器，为null时则使用自然排序

	    transient int modCount = 0; //修改队列的次数
	    
	    ......
	}

先进入开始示例代码调用的构造方法:

//示例代码中传入了Comparator对象,所以这里comparator不为null
public PriorityQueue(Comparator<? super E> comparator) {
		//这里的DEFAULT_INITIAL_CAPACITY即为前面所说的11
        this(DEFAULT_INITIAL_CAPACITY, comparator);//调用另外一个构造方法(即接下来这个)
    }

进入另外一个构造方法:

public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {
        if (initialCapacity < 1)//初始化容量如果小于1，抛异常
            throw new IllegalArgumentException();
        //初始化部分全局变量
        this.queue = new Object[initialCapacity];//创建一个容量为11的数组对象并赋给queue
        this.comparator = comparator;
    }

到这里第一段代码分析完毕，主要实现的是一些对象的创建和全局变量的初始化。

4.3 第二段代码分析：

siftUp过程图解，帮助理解：

分析queue.add(1);//将指定的元素插入此优先队列：
先进入add方法：这里只是简单的调用一下offer(e)方法

public boolean add(E e) {//e为要插入的元素
        return offer(e);
    }

进入offer(E e)方法：这里是向队列插入元素的具体实现

public boolean offer(E e) {//e为要插入的元素
        if (e == null)//表示不允许放入null元素
            throw new NullPointerException();
        modCount++;//修改队列次数+1
        int i = size;//size为队列(或称为数组)的元素个数
        //queue.length为数组容量(刚开始是11)
        if (i >= queue.length)//如果数组的元素个数大于等于数组容量
            grow(i + 1);//进行扩容
        size = i + 1;//元素个数+1
        if (i == 0)//表示当前插入的是第一个元素
            queue[0] = e;//将待插入的元素e赋给数组第一项(也为该二叉树的根节点)
        else
        	//进行调整
            siftUp(i, e);//i插入的位置，e要插入的元素
        return true;
    }

显然我们第一次执行插入操作，是还不需要扩容的，但是我们还是来看一下扩容方法grow(i + 1)具体是如何实现的：
这里的扩容其实就是再申请一个容量更大的数组，并将原数组的元素复制到容量更大的新数组

private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        //如果旧数组容量小(小的程度是小于64)，则容量增加2；否则增加50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // 判断是否超过最大容量值，设置最高容量值
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);//复制数组元素
    }

看完grow(i + 1)后，我们顺着执行顺序来到调整方法siftUp(i, e)：

private void siftUp(int k, E x) {//k为插入位置，x为要插入的项
        if (comparator != null)
        	//采用自定义排序，从小到大或从大到小(根据你的具体实现逻辑)
        	//这里我们实现的是从小到大
        	//因为示例代码中传入了Comparator对象，所以comparator不为null，待会走此方法
            siftUpUsingComparator(k, x);
        else
        	//采用默认自然排序，从小到大
            siftUpComparable(k, x);
    }

默认调整方式的实现：

@SuppressWarnings("unchecked")
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;//parent=(k-1)/2
            Object e = queue[parent];
            //默认自然排序，从小到大
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

自定义比较器的实现，调整方式，源码如下：
继siftUp(i, e)之后要走的下面这个方法(这里分该方法时是从实现小根堆的方向来讲的，如果实现的是大根堆，意思也是差不多的，就不累赘了)，

	/**
	 * 在k位置插入项目x，通过向上提升x直到它大于或等于其父节点，或者是根节点，来保持堆结构不变，
	 * 即将值小的元素向上提升，即小根堆
	 */
@SuppressWarnings("unchecked")
    private void siftUpUsingComparator(int k, E x) {//k为插入位置，x为要插入的项
        while (k > 0) {//实现值小的元素向上提升的具体代码
        	//">>>”表示无符号右移运算符。高位补0,这里即parent=k-1/2=0，parent最小值为0，
        	//所以退出循环的条件一定是k=0或者在if的时候break掉
            int parent = (k - 1) >>> 1;//获取当前节点x的父节点的下标
            Object e = queue[parent];//取出x的父节点赋给e
            //这里走前面我们示例代码中重写的compare方法
            //根据重写的compare方法实现，如果if成立则表示x的值大于e的值
            if (comparator.compare(x, (E) e) >= 0)
                break;
            /**
             * 这里表示前面比较结果是<0,则表明x的值小于其直接父节点e的值，说明x的位置要向上提升，
             * 则将父节点元素e的位置向下置到k位置
             */
            queue[k] = e;
            k = parent;
        }
        /**
         * 若前面的while循环是因为k=0退出的话，则这里表示将待插入元素x置于根结点，元素x的值最小；
         * 如果是因为break，则x的位置是k（此k小于等于前面的k），根节点以下的位置。
         */
        queue[k] = x;
    }

到此queue.add(1)分析完，完成了元素的插入并重新调整了元素位置，保持堆结构不变。

4.4 第三段代码分析：

siftDown过程图解：

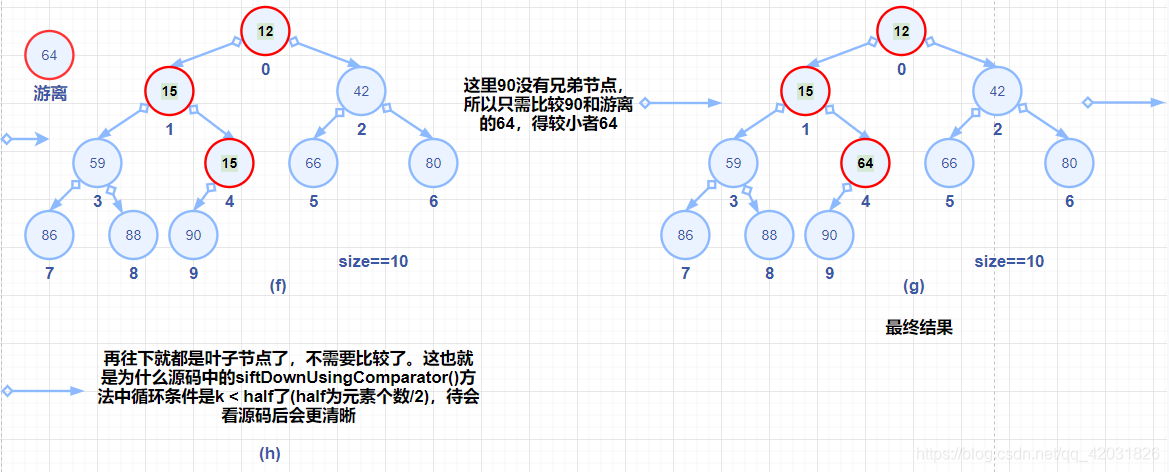
分析queue.poll();//取出元素(其实和第二段的分析差不多的)。
我们来看看其具体实现，先进入poll()方法:

@SuppressWarnings("unchecked")
    public E poll() {
        if (size == 0)
            return null;
        int s = --size;//元素个数减1
        modCount++;//改变次数加1
        E result = (E) queue[0];//取出首元素(即根节点元素)
        E x = (E) queue[s];//取出尾元素
        queue[s] = null;//将尾元素位置置为null
        if (s != 0)
            siftDown(0, x);//重新调整数组中元素顺序，从而保证推结构
        //将根节点元素返回
        //这里可以看到每次我们从队列获取值时，总是先将根节点元素获取出来
        //这也就是为什么我们poll()出来的元素是排好顺序的
        return result;
    }

这里我们看到和上面siftUp极度相似的代码，如出一辙。

private void siftDown(int k, E x) {//k为0，x为尾元素
        if (comparator != null)
            siftDownUsingComparator(k, x);//传入了Comparator对象，执行这里
        else
            siftDownComparable(k, x);
    }

@SuppressWarnings("unchecked")
    private void siftDownUsingComparator(int k, E x) {//k为0，x为尾元素
        int half = size >>> 1;//无符号右移一位，即half=size/2
        //第一次：0<half。因为只需用尾元素与非叶子节点进行比较即可，所以这里以k<half为循环条件
        while (k < half) {
            int child = (k << 1) + 1;//假设左子结点最小,child=k*2+1,
            Object c = queue[child];//获取左子节点元素
            int right = child + 1;//右子节点下标
            if (right < size &&//如果右子节点下标小于数组长度
                comparator.compare((E) c, (E) queue[right]) > 0//左右子节点的值进行比较)
                c = queue[child = right];//右子节点的值小，则将该值赋给c
            if (comparator.compare(x, (E) c) <= 0)
                break;//尾元素x的值比根节点的子节点c的值小，则break退出循环，执行外面的queue[k] = x;
            queue[k] = c;//将较小的元素c赋给数组的k位置
            k = child;
        }
        queue[k] = x;
    }

5：总结

通过上面的源码，可以看出几乎每次从队列中插入或取出元素都需要对队列进行调整，以保证队列的实现堆的父节点的值总是大于等于其子节点的值(小根堆也叫最小堆)，或是小于等于其子节点的值(大根堆也叫最大堆)，保证其推结构。
PriorityQueue并不是线程安全队列，因为offer/poll都没有对队列进行锁定操作，所以，如果要拥有线程安全的优先队列，需要额外进行加锁操作。
ps:码字有点多，望各位大神指正小弟的各种错误，一起交流！！！