SVM原理理解
SVM主要用途
SVM还是属于监督学习的范围,主要即用于解决分类问题。但是之前我们已经知道了Logistic回归等分类方法,为什么还要使用SVM,因为SVM有这样一个特性:大间隔分类!
如何理解“大间隔”分类?
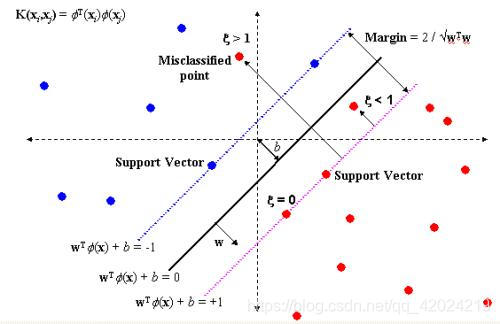
我们来直观感受一下“大间隔”。看到上图,红色为正类,蓝色为负类,中间的黑线是决策边界,而红线与黑线均为与黑线相隔一定距离的界线。在SVM训练的过程中,其会尽可能保证在最后训练输出的模型中,样本中的正类点保持在红线右边,样本中的负类点保持在蓝线左边,同时红线、蓝线与黑线的距离要达到尽可能的大!!!
对于SVM,有个略微八股的说明:支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上的,根据有限的样本信息在模型的复杂性(即对特定训练样本的学习精度)和学习能力(即无错误地识别任意样本的能力)之间寻求最佳折衷,以期获得最好的推广能力(或称泛化能力)。
什么是VC维?
所谓VC维是对函数类的一种度量,可以简单的理解为问题的复杂程度,VC维越高,一个问题就越复杂。正是因为SVM关注的是VC维,后面我们可以看到,SVM解决问题的时候,和样本的维数是无关的(甚至样本是上万维的都可以,这使得SVM很适合用来解决文本分类的问题,当然,有这样的能力也因为引入了核函数)。
什么是结构风险?我们先来看一段对机器学习中风险一词的说明:
这个与问题真实解之间的误差,就叫做风险(更严格的说,误差的累积叫做风险)。我们选择了一个假设之后(更直观点说,我们得到了一个分类器以后),真实误差无从得知,但我们可以用某些可以掌握的量来逼近它。最直观的想法就是使用分类器在样本数据上的分类的结果与真实结果(因为样本是已经标注过的数据,是准确的数据)之间的差值来表示。这个差值叫做经验风险Remp(w)。以前的机器学习方法都把经验风险最小化作为努力的目标,但后来发现很多分类函数能够在样本集上轻易达到100%的正确率,在真实分类时却一塌糊涂(即所谓的推广能力差,或泛化能力差)。此时的情况便是选择了一个足够复杂的分类函数(它的VC维很高),能够精确的记住每一个样本,但对样本之外的数据一律分类错误。回头看看经验风险最小化原则我们就会发现,此原则适用的大前提是经验风险要确实能够逼近真实风险才行(行话叫一致),但实际上能逼近么?答案是不能,因为样本数相对于现实世界要分类的文本数来说简直九牛一毛,经验风险最小化原则只在这占很小比例的样本上做到没有误差,当然不能保证在更大比例的真实文本上也没有误差。
统计学习因此而引入了泛化误差界的概念,就是指真实风险应该由两部分内容刻画,一是经验风险,代表了分类器在给定样本上的误差;二是置信风险,代表了我们在多大程度上可以信任分类器在未知文本上分类的结果。很显然,第二部分是没有办法精确计算的,因此只能给出一个估计的区间,也使得整个误差只能计算上界,而无法计算准确的值(所以叫做泛化误差界,而不叫泛化误差)。
那结构风险呢?
置信风险与两个量有关,一是样本数量,显然给定的样本数量越大,我们的学习结果越有可能正确,此时置信风险越小;二是分类函数的VC维,显然VC维越大,推广能力越差,置信风险会变大。
泛化误差界的公式为:
R(w) ≤ Remp(w) + Ф(n/h)
公式中R(w)就是真实风险,Remp(w)就是经验风险,Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。
SVM正是这样一种努力最小化结构风险的算法。
(有机会找找VC维理论更专业的paper看看)
所以上面我介绍的“大间隔”直观上可以理解为SVM为了保证结构风险最小化所持有的一种特性:这样它能在尽可能地保证拟合样本点,同时在决策边界处尽可能地减小风险,保证不误判将要预测的数据!SVM的特性使得它得到了广泛的应用。
SVM原理
基本概念与符号定义
| 符号 | 说明 |
|---|---|
| x ( i ) x^{(i)} x(i) | 第 i 个样本点的特征值向量 |
| y ( i ) y^{(i)} y(i) | 第 i 个样本点的实际值(实际所属类别) |
| γ ( i ) ^ \hat{\gamma^{(i)}} γ(i)^ | 第 i 个样本点距决策边界的距离 |
| γ ( i ) \gamma^{(i)} γ(i) | 第 i 个样本点距决策边界的几何距离 |
| γ ^ \hat{\gamma} γ^ | 最小距离 |
| γ \gamma γ | 最小几何距离 |
| ω \omega ω | 权值向量 |
| b b b | 偏置值 |
| K ( x 1 , x 2 ) K(x_1, x_2) K(x1,x2) | 核函数 |
| h w , b ( x ) ) h_{w, b}(x)) hw,b(x)) | 最终训练出的分类器(预测函数) |
-
以下关于SVM的叙述基于二分类(即只有两个类别的分类)问题展开。
-
在SVM中,类别的标记值即 y ( i ) y^{(i)} y(i)并不像
Logistic回归那样按照负类为0,正类为1或正负类为何值不影响的情况了,而是定义正类为1,负类为-1,后面我们会看到这样定义有什么用处。 -
在
Logistic回归中,权值向量是定义为: [ θ 0 , θ 1 , . . . , θ n ] T [\theta_0, \theta_1,..., \theta_n]^{T} [θ0,θ1,...,θn]T
而在SVM中, ω \omega ω 其实就相当于 [ θ 1 , . . . , θ n ] T [\theta_1,..., \theta_n]^{T} [θ1,...,θn]T, b b b 相当于
θ 0 \theta_0 θ0, b b b 被单独拿出来作为偏置值了,训练时真正训练的是 ω \omega ω, b b b
在后面代入一些样本点的值就可以算出来了。 -
决策边界即为 ω T x ( i ) + b = 0 \omega^{T}x^{(i)} + b = 0 ωTx(i)+b=0这条直线【“直线”这一说法只适用于二维的情况,即 x ( i ) x^{(i)} x(i) 的长度为2的情况;更普遍的讲,它应该叫**超平面**】
-
对于线性分类器,定义为 h w , b = g ( ω T x ( i ) + b ) h_{w, b}=g(\omega^{T}x^{(i)} + b) hw,b=g(ωTx(i)+b),
给定一个输入 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)):
当 ω T x ( i ) + b > 0 \omega^{T}x^{(i)} + b>0 ωTx(i)+b>0时, g ( ω T x ( i ) + b ) = 1 g(\omega^{T}x^{(i)} + b)=1 g(ωTx(i)+b)=1,表示预测其为正类;
当 ω T x ( i ) + b < 0 \omega^{T}x^{(i)} + b<0 ωTx(i)+b<0时, g ( ω T x ( i ) + b ) = − 1 g(\omega^{T}x^{(i)} + b)=-1 g(ωTx(i)+b)=−1,表示预测其为负类;
当 ω T x ( i ) + b = 0 \omega^{T}x^{(i)} + b=0 ωTx(i)+b=0时,看你自己如何定义,有的人会定义为拒绝预测的情况,有的人会定义预测其为正类,有的人会定义预测其为负类。
而对于非线性的分类器,则要视具体的核函数形式而定。
几何距离与距离的概念
给定一个样本点 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i








 SVM是一种监督学习算法,主要用于分类,以其大间隔分类特性著称。通过最大化间隔来减少错误分类的风险,从而提高模型的泛化能力。本文详细介绍了SVM的原理,包括基本概念、决策边界的优化目标以及核函数的使用,揭示了SVM在处理线性及非线性问题时的优势。
SVM是一种监督学习算法,主要用于分类,以其大间隔分类特性著称。通过最大化间隔来减少错误分类的风险,从而提高模型的泛化能力。本文详细介绍了SVM的原理,包括基本概念、决策边界的优化目标以及核函数的使用,揭示了SVM在处理线性及非线性问题时的优势。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 3776
3776

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








