线段树

最新推荐文章于 2025-03-25 21:45:46 发布

原创最新推荐文章于 2025-03-25 21:45:46 发布 · 195 阅读

0 ·

CC 4.0 BY-SA版权

知识点梳理同时被 2 个专栏收录

4 篇文章

订阅专栏

（开飞机）集训

4 篇文章

订阅专栏

本文详细介绍了线段树的数据结构及其实现方法，包括如何通过递归实现区间查询和点更新操作，并展示了如何利用偏移量进行高效的大批量区间更新。

感谢老刘……

模板……

线段树

——区间维护的完全二叉树

支持操作：区间查询最值、修改点值

线段树和完全二叉树的区别在哪里呢？

线段树的每个节点表示的是一个区间，左右子树表示的是这个区间的左半边和右半边。

将需要处理的区间不相交的若干小区间。

[a,b]的左子树对应线段[a,(a+b)>>1]，右子树对应线段[((a+b)>>1)+1,b]

生动形象的图示：

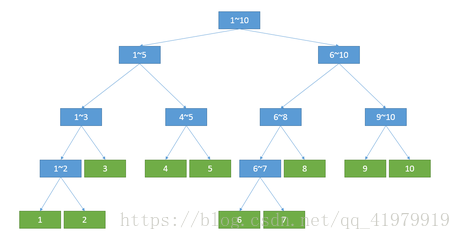
如图，得：

[1,L]的线段树深度不超过log₂(L-1)+1,节点数不超过2L个
i号单元的左孩子储存在2*i号单元，右孩子储存在2*i+1号单元。
包含n个点的线段树，一维数组不需超过4*n。

代码：（注意：以下x，y都是全局变量）

由于操作需要往下深入，所以这里用的是递归

定义

struct node
{
	//int l;//从左端点开始的连续最大长度
	//int r;//以右端点结束的连续最大长度
	int maxx,delta;//区间内最大值和偏移量
}tree[maxn*4];

查询从x到y这个区间的最大值

int search(int left,int right,int root)
{
	int mid,templ,tempr;
	if(x>right||y<left)return -20000000;
	if(x<=left&&right<=y)return tree[root].maxx;
	mid=(left+right)>>1;
	templ=search(left,mid,root*2);
	tempr=search(mid+1,right,root*2+1);
	return max(templ,tempr);
}

把第x个点的值改为y

void updata(int left,int right,int root)
{  
	int mid;
	if(y<left||x>right)return;
	if(left==right){tree[root].maxx=y;return;}
	mid=(left+right)>>1;
	updata(left,mid,root*2);
	updata(mid+1,right,root*2+1);
	tree[root].maxx=max(tree[root*2].maxx,tree[root*2+1].maxx);
}

用上偏移量就是高端操作了（如果要修改[a,b]的值时，如果传递到了一个区间[c,d]完全包含在[a,b]里，就不用往下传递了，只需在查询时顺便往下传递或者回溯时将偏移量加到查询的值里，这样保证了线段树的高效）

查询

int search(int left,int right,int root)
{
	if(x>right||y<left)return -20000000;
	if(x<=left&&right<=y)return tree[root].maxx;
	int mid=(left+right)>>1;
    int delta=tree[root].delta;
	tree[root*2].delta+=delta;tree[root*2].maxx+=delta;
	tree[root*2+1].maxx+=delta;tree[root*2+1].delta+=delta;
	tree[root].delta=0;
	int templ=search(left,mid,root*2);
	int tempr=search(mid+1,right,root*2+1);
	return max(templ,tempr);
}

修改

void updata(int left,int right,int root)
{
	if(y<left||x>right)return;
	if(x<=left&&y>=right){tree[root].maxx++;tree[root].delta++;return;}
	int mid=(left+right)>>1;
    int delta=tree[root].delta;
	tree[root*2].delta+=delta;tree[root*2].maxx+=delta;
	tree[root*2+1].maxx+=delta;tree[root*2+1].delta+=delta;
	tree[root].delta=0;
	updata(left,mid,root*2);
	updata(mid+1,right,root*2+1);
	tree[root].maxx=max(tree[root*2].maxx,tree[root*2+1].maxx);
}
//search(1,n,1);updata(1,n,1);