8.2学习总结

最新推荐文章于 2025-01-07 08:49:00 发布

躺平小菜菜

最新推荐文章于 2025-01-07 08:49:00 发布

阅读量107

点赞数

分类专栏：学习总结

本文链接：https://blog.youkuaiyun.com/qq_41970610/article/details/119321542

版权

7 篇文章

订阅专栏

本文介绍了动态规划的基础概念及入门题目“三步楼梯”的解决思路，并探讨了状态转移方程的应用。此外还介绍了快速幂算法及其时间复杂度优势。通过回溯算法的基本原理和应用场景的讲解，帮助读者更好地理解动态规划问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

对于动态规划入门题目进行三步楼梯题目需要对于状态转移公式有一个熟悉的应用和掌握，今日题目转移公式dp[i] = dp[i - 1] + dp [i - 2] + dp [i - 3] 进行入门级理解，所用到的数组进行缓存。

另外对快速幂进行初步的理解，当要计算 $a^{n}$ 。如果n为偶数可以算( $a^{\frac{n}{2}}$ )的2次方算出来结果，当n为奇数时 $a^{\frac{n-1}{2}}$ 的平方，再×a 可以得出这样只需要用O(log n)的复杂度就可以计算出 $a^{n}$ 了。

当解动态规划问题的时候，需要对回溯算法有一定的了解，回溯算法简单来说就是在对数据进行遍历的过程中，即搜索寻找解时当在搜索的过程中无法继续向下继续寻找的时候，需要回到原来的出发点去重新寻找其他路径找寻解，这个过程就是回溯算法的过程。

在此过程中可能会遇到的一个问题时需要将找寻存储的撤销选择的操作，这其中需要了解的是递归算法中的一个操作范例，当去找到一个数组组合时，需要回溯到前一个点找另外的数组组合的时候需要将原有的查找记录撤销掉，当然不撤销也有方式完成就是在每一步都要重新创建一个新的list来存新遍历的数组成员。

回溯算法的模板：

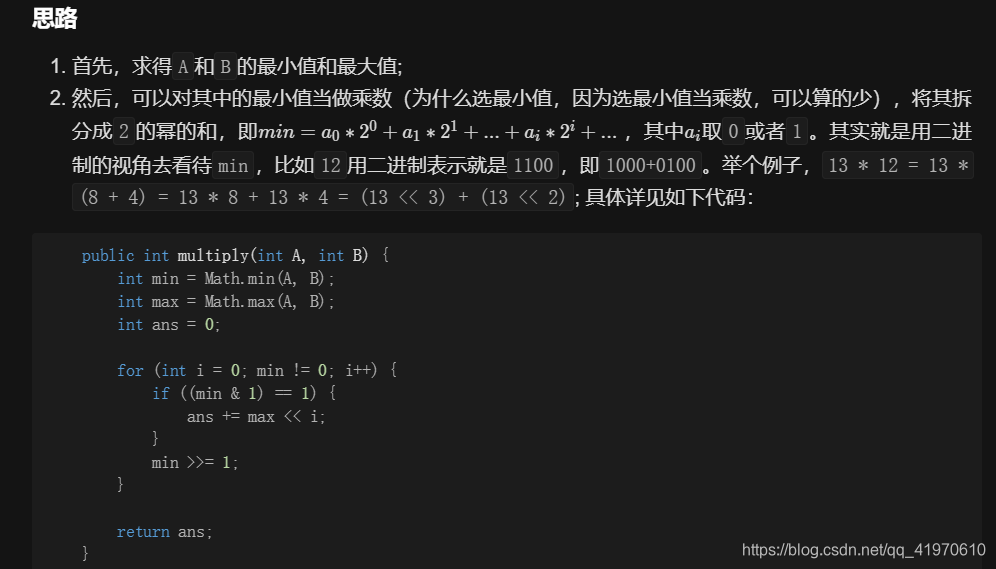
leetcode2115题中所提到的为需要将位运算应用在数乘当中，其中将所给数进行位数拆分时应对此方法的关键所在。