关于欧几里得距离的一些解释

最新推荐文章于 2025-06-26 22:38:51 发布
最新推荐文章于 2025-06-26 22:38:51 发布
阅读量8.1k 收藏 5
点赞数 2
CC 4.0 BY-SA版权
分类专栏： 机器学习之旅
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_41940950/article/details/83926312
本文深入探讨了欧几里得距离的概念及其在多维空间中的应用，解析了欧氏距离的计算公式，并介绍了其在数字图像处理，特别是图像骨架提取中的重要作用。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

最近研究多维空间下的距离，很头晕（呜呜呜呜~~~~~~~~）
正题：
在数学中，欧几里得距离或欧几里得度量是欧几里得空间中两点间“普通”（即直线）距离。使用这个距离，欧氏空间成为度量空间。相关联的范数称为欧几里得范数。较早的文献称之为毕达哥拉斯度量。

定义

在欧几里得空间中，点x =(x1,…,xn)和 y =(y1,…,yn)之间的欧氏距离为
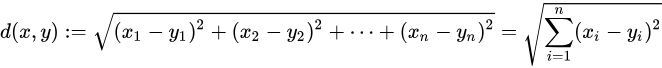
在这里插入图片描述
向量x的自然长度，即该点到原点的距离为
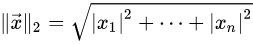
在这里插入图片描述
它是一个纯数值。在欧几里得度量下，两点之间线段最短。

计算公式

二维空间的公式
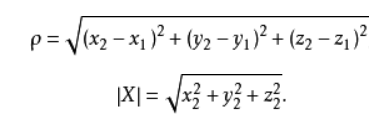
在这里插入图片描述
三维空间的公式
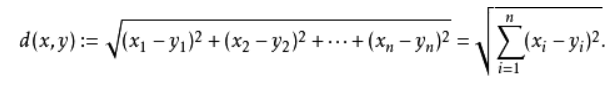
在这里插入图片描述
N维空间的公式
在这里插入图片描述

欧式距离变换

所谓欧氏距离变换，是指对于一张二值图像（在此我们假定白色为前景色，黑色为背景色），将前景中的像素的值转化为该点到达最近的背景点的距离。
欧氏距离变换在数字图像处理中的应用范围很广泛，尤其对于图像的骨架提取，是一个很好的参照

关于欧几里得距离、哈曼顿距离和闵可夫斯基距离的解释参考：
https://blog.youkuaiyun.com/qq_41940950/article/details/83858193

【AI知识点】欧几里得距离（Euclidean Distance）L2距离（L2 Distance）
AI完全体
10-02 2823
欧几里得距离（Euclidean Distance）也称 L2距离（L2 Distance），是一种常用的几何距离度量方法，用来计算两个点之间的直线距离。在二维或更高维空间中，欧几里得距离可以看作是“最短路径”的概念。它在机器学习、图像处理、模式识别、聚类分析等领域有广泛的应用。
什么是欧几里得距离（即欧氏距离，也叫欧几里得度量）
weixin_44828787的博客
10-18 1492
什么是“欧几里得距离”？
距离度量类型总结
最新发布
2501_90669630的博客
06-26 884
曼哈顿距离(Manhattan Distance，也称为 L1 距离)的定义为：在直角坐标系中，两点之间的距离是它们在各坐标轴方向上差的绝对值之和。曼哈顿距离的几何意义是"沿轴向移动的最短路径"，常用于计算两点间的最短可行路径。 在 nnn 维空间中，点 A=(a1a2⋮an)A = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}A=​a1​a2​⋮an​​​ 和点 B=(b1b2⋮bn)B = \begin{pmatrix} b_1
欧几里得距离（Euclidean Distance）公式
qq_44726330的博客
03-28 1842
dEuclideanABx2−x12y2−y12dEuclidean​ABx2​−x1​2y2​−y1​2​欧几里得距离是一种直观且广泛应用的距离度量方法，适用于多种场景。它的核心思想是计算两点之间的直线距离，简单高效，但在高维空间中可能受到“维度灾难”的影响。
欧几里得最短距离公式_老师好，关于欧几里得距离计算，有没有什么更高效的计算方式？...
weixin_35117981的博客
12-23 338
自己老师布置的一个题目：在100W个100维的向量中，取出与给定的100维的向量，欧几里得距离最小的前K个向量。我把这个问题分为了2部分，一个是计算部分，一个是统计部分。统计部分用到了索引堆，很好用！但是在计算部分，我使用最普通的计算公式，太耗费时间(8s)。所以有没有关于欧几里得距离更高效的计算方式？感谢波波老师了。long start = System.currentTimeMillis();...
欧几里得距离（欧式距离）
热门推荐
sandalphon4869的博客
02-10 5万+
文章目录一、定义二、公式 一、定义 欧几里得度量（欧氏距离） Euclidean Metric，Euclidean Distance： 指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。 比如：在二维和三维空间中的欧氏距离就是两点之间的实际距离。 二、公式 二维： ρ=(x2−x1)2+(y2−y1)2\rho=\sqrt{(x_2-x_1)^2+(y_2-y_1)^...
python 欧几里得距离练习实例
07-04
Python 机器学习 欧几里得距离
平方欧几里得距离（Squared Euclidean Distance） 和 L2 距离（欧几里得距离，Euclidean Distance）
大多_C的博客
02-05 1419
这里梯度不会因为平方根的影响而变小，梯度的大小只与点的间距成线性关系。当 ( A ) 和 ( B ) 相距较远时，分母变大，导致梯度变小。的主要区别在于它们的计算公式、梯度特性以及在深度学习中的应用。，如果你的训练过程中梯度更新不稳定，可能会收敛较慢，可以考虑。PyTorch 默认。
欧几里得距离：计算欧几里得距离为2D3DnD空间中的两点
02-15
欧氏距离 欧几里德距离是一个用于计算-友好NPM模块 在n维空间中的两个向量之间。 安装 npm install euclidean-distance --save 用法 var distance = require ( 'euclidean-distance' ) distance ( [ 0 , 0 ] , [ 1 ...
matlab开发-QAM的欧几里得距离最小值
08-28
标题中的“matlab开发-QAM的欧几里得距离最小值”指的是在MATLAB环境中，针对Quadrature Amplitude Modulation（QAM）调制技术的一种应用开发，具体是寻找接收信号与期望信号之间的欧几里得距离最小值。QAM是一种...
欧几里得最短距离公式_欧几里得度量（欧氏距离）
weixin_39955953的博客
12-23 4373
欧几里得度量，或者说欧氏距离，Euclidean Distance，这个名字来自著名的古希腊数学家欧几里得。欧几里得(公元前330年—公元前275年)，古希腊数学家。他活跃于托勒密一世(公元前364年－公元前283年)时期的亚历山大里亚，被称为“几何之父”，他最著名的著作《几何原本》是欧洲数学的基础，提出五大公设，欧几里得几何，被广泛的认为是历史上最成功的教科书。欧几里得也写了一些关于透视、圆锥曲...
OpenCV---基于欧几里得距离计算公式的图像二值化实现
12-26
OpenCV---基于欧几里得距离计算公式的图像二值化实现.具体的讲解见博客：http://blog.youkuaiyun.com/FreeApe/article/details/50409862
欧几里得距离
zbzbzzz
04-25 2266
怕忘记咯先记录一下 欧几里得距离（ Euclidean distance）也称欧式距离，它是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。 在二维和三维空间中的欧式距离的就是两点之间的距离，二维的公式是 d = sqrt((x1-x2)+(y1-y2)) 三维的公式是 d=sqrt(x1-x2)+(y1-y2)+(z1-z2)^) 推广到n维空间，欧式距离的公式是 d=sqrt( ∑(xi1-xi2)^ ) 这里i=1,2…n xi1表示第一个点的第i维坐标,xi2表示第二个点的第i维坐标
NEO4J-相似度算法04-欧几里得距离算法（euclidean）应用场景简介
lijunliang2017的博客
08-23 2021
说明：使用neo4j算法库时需引入跟neo4j数据库对应的算法库插件或自定义算法库 1.简介 欧几里德距离算法原理是计算n维坐标系中点与点之间地距离，如在三维坐标系中点A(p1,p2,p3),点B(q1,q2,q3),两个点之间得距离则为 ： , 如果在n维坐标系中，两个点得距离则变为： 根据以上特性拓展：距离越小则A点和B点重合度越高，由此可衍生出A点和B点在n维空间中距离相似度公式为： similarity = neo4j自带算法包提供了欧几里得相似度...
C/C++ 欧几里得距离算法详解及源码
希望我的博客，能帮上你解决学习中工作中所遇到的问题
05-10 5752
欧几里得距离算法（Euclidean Distance）是用于计算两个点之间的距离的一种常用方法。它基于欧几里得空间中的几何概念，计算的结果即为两点之间的直线距离。其中，(x1, y1)和(x2, y2)分别表示两个点的坐标，d表示两个点之间的距离。
距离度量 —— 欧式距离（Euclidean Distance）
繁依Fanyi的博客
06-10 3万+
欧式距离，也称为 欧几里得距离，是我们从小学、初中、高中等等乃至现在都会用到的距离度量。“两点之间线段最短” 大家都学过吧，这里只不过给换了一个高大上的英文名字，就是我们在小初高等试卷上计算距离的那个公式假设 二维平面 内有两点：a(x1,y1)a(x_{1},y_{1})a(x1​,y1​) 与 b(x2,y2)b(x_{2},y_{2})b(x2​,y2​)则二维平面的距离公式为：d12=(x1−x2)2+(y1−y2)2d_{12}=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2}
欧几里得、曼哈顿、和切比雪夫距离公式图片详解
qq_45059903的博客
08-18 3818
1. 欧几里得距离 计算公式（n维空间下） 二维：dis=sqrt( (x1-x2)^2 + (y1-y2)^2 ) 三维：dis=sqrt( (x1-x2)^2 + (y1-y2)^2 + (z1-z2)^2 ) 2.曼哈顿距离：两个点在标准坐标系上的绝对轴距总和 dis=abs(x1-x2)+(y1-y2) 如图所示，图中_A_,B_两点的曼哈顿距离为_AC+BC=4+3=7 3.切比雪夫距离：各坐标数值差的最大值 dis=max(abs(x1-x2),abs(y1-y2)) dis=max(A
欧几里得最短距离公式_#973最接近原点的 K 个点
weixin_36189159的博客
01-07 898
题目：我们有一个由平面上的点组成的列表 points。需要从中找出 K 个距离原点 (0, 0) 最近的点。(这里，平面上两点之间的距离是欧几里德距离。)你可以按任何顺序返回答案。除了点坐标的顺序之外，答案确保是唯一的。示例 1：输入：points = [[1,3],[-2,2]], K = 1输出：[[-2,2]]欧几里得距离，事实上就是二维平面直角坐标系两点的距离。任意一个点，它到原...
计算欧几里得距离
03-27
### 实现欧几里得距离计算 以下是基于 Python 编程语言实现的欧几里得距离计算方法。该函数支持任意维度的空间，能够处理 n 维向量间的距离计算。 ```python import numpy as np def calculate_euclidean_distance(point_a, point_b): """ 计算两点之间的欧几里得距离 参数: point_a - 数组或列表形式表示的第一个点坐标 point_b - 数组或列表形式表示的第二个点坐标 返回值: 距离 - 浮点数，代表两点多维空间中的欧几里得距离 """ if len(point_a) != len(point_b): raise ValueError("输入的两个点必须具有相同的维度") # 输入校验[^1] distance = np.sqrt(np.sum((np.array(point_a) - np.array(point_b)) ** 2)) return distance ``` 上述代码通过 `numpy` 库实现了高效的数值运算，利用了矢量化操作来简化复杂度并提升性能。此方法不仅限于二维或三维空间，在更高维度的数据集上同样适用[^4]。 #### 使用示例 下面展示了如何调用以上定义好的函数来进行不同场景下的欧氏距离求解： ##### 一维情况 ```python point_x = [3] point_y = [7] result = calculate_euclidean_distance(point_x, point_y) print(f"一维情况下 {point_x} 和 {point_y} 的欧几里得距离为：{result}") ``` ##### 二维情况 ```python point_p = [1, 2] point_q = [4, 6] distance_2d = calculate_euclidean_distance(point_p, point_q) print(f"{point_p} 和 {point_q} 在二维平面上的距离为：{distance_2d}") # 输出应接近5.0依据具体浮点精度设置而定. ``` ##### 高维（如四维） ```python vector_u = [1, 2, 3, 4] vector_v = [-1, -2, -3, -4] high_dimensional_dist = calculate_euclidean_distance(vector_u, vector_v) print(f"高维向量 {vector_u} 和 {vector_v} 的欧几里得距离为：{high_dimensional_dist}") ``` 这种方法遵循通用原则，即当给定点 A=(a₁,a₂,…,an) 及 B=(b₁,b₂,…,bn)，则它们间欧几里德间距 d(A,B)=√[(ai-bi)^2]+...+(an-bn)^2][^3].
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值