数据结构与算法（C语言严蔚敏）三_数据结构c语言版严蔚敏一书中的算法可以用什么编译软件执行-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_41935112/article/details/128511715

本文详细介绍了栈和队列的基本概念、特性以及C语言中的实现，包括顺序栈和链式栈的创建、入栈、出栈、取栈顶元素等操作，同时也讨论了顺序队列和链式队列的初始化、入队、出队和队列长度的计算。此外，文章还提到了栈和队列在数制转换、括号匹配等实际问题中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

有误的地方还请大家指出来，我会一一改正，也会在评论区置顶更正的记录；
如果是因为不同的教材导致的错误，请把教材名、著作者、版次一并提供，供大家一起督促一起学习，本篇参考的教材是《数据结构与算法 (C语言) 严蔚敏》，这也是我大学教材。
程序的逻辑大同小异，本篇只是针对参考的教材做出的记录，不具有代表性。
保持良好的网络教学环境，请不要随意断章取义、复制粘贴。
老师教材里面函数形参用 & 引用的都是 C++ 编译器，不是 C 。教材是这样我就不改了，注意区分 * 指针。

栈和队列

1. 栈

栈的相关概念

栈：是仅在表尾进行插入和删除操作的线性表。
栈的特点：先进后出（FILO, First-In Last-Out）或（LIFO）。
栈顶：top，允许插入、删除的一端。
栈底：bottom，栈顶的另一端。
空栈：不含任何数据元素的栈。
下溢：当空栈时再做退栈运算将产生溢出称为下溢。下溢是正常现象，因为栈的初态或终态都是空栈，所以下溢常用作程序控制转移的条件。
栈满：
栈的实现：
1. 将栈底的位置固定在数组的最左端或者最右端。
2. 栈顶的位置用一个整形指针 top 来指示，top 栈顶指针随着进栈和退栈操作而变化。
3. 通常 top 指针有 0 和 -1 两种初值。
n 个元素的出栈方式有 N 种，N 与 n 的公式如下：

顺序栈

顺序栈 c 语言的定义

#define STACK_INIT_SIZE 3 //栈存储空间初始分配量
#define STACKINCREMENT 2 //栈存储空间分配增量
#define OK 1
#define ERROR 0
#define OVERFLOW -1

typedef int SElemType;
typedef int status;

typedef struct { //顺序栈的定义 没有定义数组 只能靠指针来访问
	SElemType* base;
	SElemType* top;
	int stacksize;//当前已分配的存储空间
}SqStack;

status InitStack(SqStack &S); //构造一个空栈S
status Push(SqStack& S, SElemType e);//入栈
status Pop(SqStack& S, SElemType& e); //出栈
status GetTop(SqStack& S, SElemType e); //取栈顶元素
status StackEmpty(SqStack& S); //判断栈S是否为空

栈的初始化

//构造一个空栈S
status InitStack(SqStack& S) {
	S.base = (SElemType*)malloc(STACK_INIT_SIZE * sizeof(SElemType)); //分配存储空间
	if (!S.base) exit(OVERFLOW); //存储分配失败
	S.top = S.base;
	S.stacksize = STACK_INIT_SIZE;
	return OK;
}

入栈

// 插入元素e为新的栈顶元素
status Push(SqStack &S,SElemType e){
	if(S.top-S.base>=S.stacksize)
	{ //栈满，追加存储空间
		S.base=(SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));
		if(!S.base) exit(OVERFLOW); //存储分配失败
		S.top=S.base+S.stacksize;
		S.stacksize+=STACKINCREMENT;
	}
	*S.top++=e; // *
	return OK;
}

出栈

status Pop(SqStack& S, SElemType& e) {
	//若栈不空，则删除S的栈顶元素，用e返回其值并返回OK；否则返回ERROR
	if (S.top == S.base) return ERROR;
	e = *--S.top;  // *
	return OK;
}

取栈顶元素

status getTop(SqStack S, SElemType& e) {
	//若栈不空，则取出S的栈顶元素，用e返回其值并返回OK；否则返回ERROR
	if (S.top == S.base) return ERROR;
	e = *(S.top - 1); // *
	return OK;
}

判断栈是否为空

status StackEmpty(SqStack S) {
	if (S.top == S.base)
		return OK;
	else return ERROR;
}

求栈的长度

int size(SqStack S)
{
return （S.top-S.base);
}

链式栈

进栈操作：p->next=top;top=p;；出栈操作：p=top;top=top->next;free(p);。

链栈的定义

void initStack(LiStack* s)
{
	s=(LiStack*)malloc(sizeof(LiStack));
	s->next = NULL;
}

销毁栈

释放栈s占用的全部存储空间。

void DestroyStack(LiStack* s)
{
	LiStack* p = s, * q = s->next;
	while (q != NULL)
	{
		free(p);
		p = q;
		q = p->next;
	}
	free(p); //此时p指向尾节点
}

判断栈是否为空

//栈s为空的条件是s->next = NULL，即单链表中没有数据节点。
bool StackEmpty(LiStack * s)
{
	return (s->next = NULL);
}

进栈Push

void Push(LiStack* s, ElemType e)
{
	LiStack* p;
	p = (LiStack*)malloc(sizeof(LiStack));
	p->data = e; //新建元素e对应的节点p
	p->next = s->next; //插入p节点作为开始节点
	s->next = p;
}

出栈

bool Pop(LiStack* s, ElemType& e)
{
	LiStack* p;
	if (s->next == NULL) //栈空的情况
		return false;
		p = s->next; //p指向开始节点
	e = p->data;
	s->next = p->next; //删除p指向节点
	free(p); //释放p节点
	return true;
}

取栈顶元素

// 在栈不为空的条件下，将头结点后继数据节点的数据域赋给e。
bool GetTop(LiStack* s, ElemType& e)
{
	if (s->next == NULL) //栈空的情况
		return false;
	e = s->next->data; //取首节点的值
	return true;
}

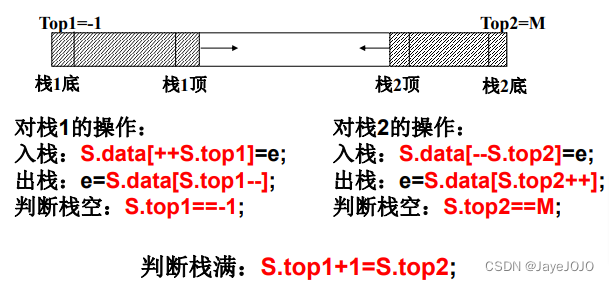
共享栈

对于两个相同类型的栈，可以在一个空间中定义两个栈，能最大限度地利用其开辟的存储空间。

栈的应用一：数制转换

略

栈的应用之二：括号匹配

略

栈的应用之三：行编辑程序

略

栈的应用之四：表达式求值

略

2. 队列

队列的相关概念

队尾：rear，允许插入的一端。
队头：front，允许删除的一端。
队列的特征：先进先出，FIFO（First In First Out）。
队列空间地址：rear 指针不等于 front 指针时。
空队列：rear 指针等于 front 指针时。
下溢：当空队列时执行出队操作，将产生下溢。
上溢：也称为假性上溢，当空队列时执行进队操作，将产生上溢。
假溢出：当空队列且队列空间用完时，执行入队会产生假溢出。
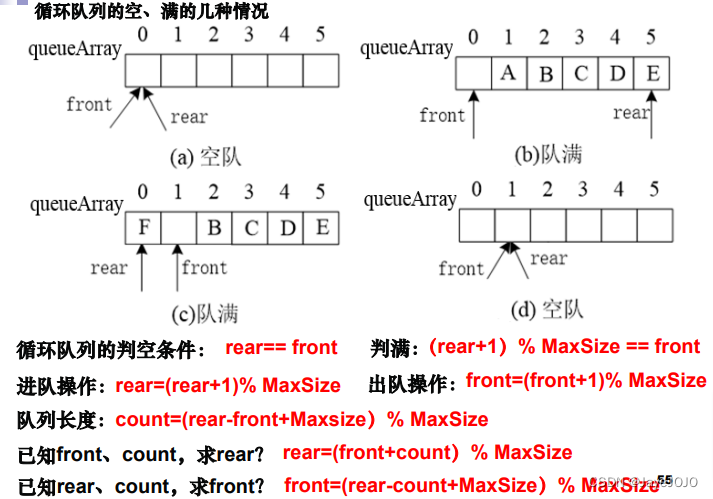
循环队列：为解决假溢出，使队头和队尾逻辑上相连。队头、队尾指针加 1 时用取模运算实现循环。
- 但此时出现队满条件( rear == front ) 与队空条件( rear == front) 无法区分的问题。
- 解决方案为：用队列中一个元素空间来做标记，使队列头指针在队尾指针的下一个位置。此时队满条件((rear+1)%M==front) 和队空( front == rear ) 已经区分开了。

顺序队列

定义队列

#define MAXSIZE 10
typedef int QElemType;
typedef int Status;
typedef struct {
	QElemType* base;//初始化的动态分配存储空间
	int front; //头指针，若队列不为空，指向队列头元素
	int rear; //尾指针，若队列不为空，指向队列尾元素的下一个位置
}SqQueue;

初始化队列

Status InitQueue(SqQueue* Q) {
	// 队列初始化
	Q->base = (QElemType*)malloc(MAXSIZE
		* sizeof(QElemType));
	if (!Q->base) return ERROR;
	Q->front = Q->rear = 0;
	return OK;
}

入队

Status EnQueue(SqQueue* Q, QElemType e) {
	// 将元素e插入队列Q的队尾
	//若队列满，进队失败，为什么不动态分配空间？
	if ((Q->rear + 1) % MAXSIZE == Q->front) return ERROR;
	Q->base[Q->rear] = e;
	// 修改队尾指针
	Q->rear = (Q->rear + 1) % MAXSIZE;
	return OK;
}

出队


Status DeQueue(SqQueue* Q, QElemType* e)
{ //删除队列Q的队首元素，并用e带回
// 若队空，出队失败
	if (Q->front == Q->rear) return ERROR;
	*e = Q->base[Q->front];
	//修改队首指针
	Q->front = (Q->front + 1) % MAXSIZE;
	return OK;
}

取头元素

Status GetHead(SqQueue* Q, QElemType* e) {
	//取出队列Q的队首元素，并用e带回
	// 若队空，提取失败
	if (Q->front == Q->rear) return ERROR;
	*e = Q->base[Q->front];
	//不修改队首指针
	return OK;
}

非空判断

bool IsEmpty(SqQueue Q)
{
	return Q.front == Q.rear;
}

求队列长度

// 队列长度
int getLength(SqQueue Q)
{
	return (Q.rear - Q.front + MAXSIZE) % MAXSIZE;
}

遍历队列

void OutputQueue(SqQueue Q)
// 输出队列中元素
{
	while (Q.front != Q.rear) { // 如果队列非空
		printf("%d ", Q.base[Q.front]);
		Q.front = (Q.front + 1) % MAXSIZE;
	}
	printf("\n");
}

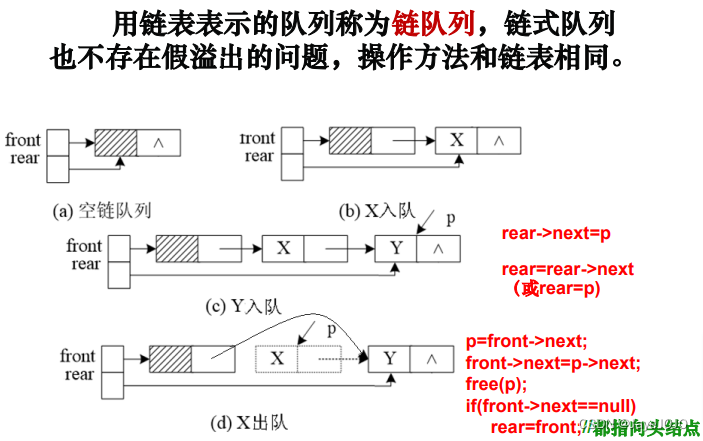
链式队列

在这里插入图片描述

队列应用之一：树的层次遍历

略

队列应用之二：杨辉三角形的输出

略

队列应用之三：模拟服务台前的排队现象问题

略

队列应用之四：迷宫寻路

略

总结

部分练习题

在这里插入图片描述

写出下列程序段的输出结果（栈的元素类型SElemType为char）:


void main()
{
	Stack S;
	char x, y;
	InitStack(S);
	x = ‘c’; y = ‘k’;
	Push(S, x); Push(S, ‘a’); Push(S, y);
	Pop(S, x); Push(S, ‘t’); Push(S, x);
	Pop(S, x); Push(S, ‘s’);
	while (!StackEmpty(S))
	{
		Pop(S, y);
		printf(y);
	}
}

答案：stac

简述以下算法的功能（栈的元素类型SElemType为int）。

status algo1(Stack S)
{
	int i, n, A[255];
	n = 0;
	while (!StackEmpty(S))
	{
		n++;
		Pop(S, A[n]);
	}
	for (i = 1; i <= n; i++)
		Push(S, A[i] + 1);
}

答案：栈中的数据元素加1逆置;

简述以下算法的功能（栈的元素类型SElemType为int）。

status algo1(Stack S)
{
	int i, n, A[255];
	n = 0;
	while (!StackEmpty(S))
	{
		n++;
		Pop(S, A[n]);
	}
	for (i = 1; i <= n; i++)
		Push(S, A[i] + 1);
}

答案：如果栈中存在元素e，将其从栈中清除

题：

1 、若一个栈以向量V[1…n]存储，初始栈顶指针top设为n+1，则元素x进栈的正确操作是( )。
A．top++; V[top]=x;
B．V[top]=x; top++;
C．top–; V[top]=x;
D．V[top]=x; top–;

2、链式栈结点为：(data,link)，top指向栈顶。若想摘除栈顶结点，并将删除结点的值保存到x中,则应执行操作（）。
A．x=top->data;top=top->link；
B．top=top->link;x=top->link；
C．x=top;top=top->link；
D．x=top->link；

答案：1、C ；2、A

写出以下程序段的输出结果（队列中元素类型QElemType为char）。


void main()
{
	Queue Q;
	InitQueue(Q);
	char x = ‘e’, y = ‘c’;
	EnQueue(Q, ‘h’);
	EnQueue(Q, ‘r’);
	EnQueue(Q, y);
	DeQueue(Q, x);
	EnQueue(Q, x);
	DeQueue(Q, x);
	EnQueue(Q, ‘a’);
	While(!QueueEmpty(Q))
	{
		DeQueue(Q, y);
		cout << y;
	}
}

答案：cha

简述以下算法的功能（栈和队列的元素类型均为int）。


void algo3(Queue& Q)
{
	Stack S;
	int d;
	InitStack(S);
	while (!QueueEmpty(Q))
	{
		DeQueue(Q, d);
		Push(S, d);
	}
	while (!StackEmpty(S))
	{
		Pop(S, d);
		EnQueue(Q, d);
	}
}

答案：队列逆置

1、设栈S和队列Q的初始状态为空，元素e1、e2、e3、e4、e5和e6依次进栈S，一个元素出栈后立即进入Q，若6个元素出队的顺序是e2、e4、e3、e6、e5和e1，则栈S的容量至少是（）。
A.2
B.3
C.4
D.6

2、为增加内存空间利用率和减少溢出可能性，当两个栈共享一片连续内存空间时，应将两个栈的（①）分别设在这片内存空间的两端，这样当（②）时，才产生上溢。
① { A. 长度 B. 深度 C. 栈顶 D.栈底 }
② { A. 两个栈的栈顶同时到达栈空间的中心点
B. 其中一个栈的栈顶到达栈空间的中心点
C. 两个栈的栈顶在栈空间的某一位置相遇
D. 两个栈均不为空，并且一个栈的栈顶到达另外一个栈的栈底 }

答案：①B ；②D,C
8. 设计一个算法利用顺序栈判断一个字符串是否是对称串。所谓对称串是指从左向右读和从右向左读的序列相同。

Bool symmetry(ElemType str[]) {
	int i; ElemType e; SqStack* st;
	InitStack(st); //初始化栈
	for (i = 0; str[i] != ‘\0’; i++) //将串所有元素进栈
		Push(st, str[i]);
	for (i = 0; str[i] != ‘\0’; i++)
	{
		Pop(st, e); //退栈元素e
		if (str[i] != e) //若e与当前串元素不同则不是对称串
		{
			DestroyStack(st); //销毁栈
			return false;
		}
	}
	DestroyStack(st); return true;
}