深度优先搜索（DFS）和广度优先搜索（BFS）

深度优先遍历（DFS）
主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底…，不断递归重复此过程，直到所有的顶点都遍历完成；下面使用深度优先遍历一颗树：

1、从根节点 1 开始遍历，它相邻的节点有 2，3，先遍历节点 2，2的相邻节点有4、5，遍历 2 的子节点 4，4没有相邻节点，结束向下遍历

2、上图中一条路已经走到底(4是叶子节点，再无可遍历的节点)，此时就从 4 回退到上一个节点 2，看下节点 2 是否还有除 4 以外的节点，2 有除 4 以外的节点 5，所以从节点 3 开始进行深度优先遍历，5相邻的节点有 7，8，先遍历节点 7，7的相邻节点有10，遍历 7 的子节点 10，10没有相邻节点，结束向下遍历

3、同理从 10 开始往上回溯到 7, 7 没有除 10 以外的子节点，再往上回溯，发现 5 有除 6 以外的子点 8，所以此时会遍历 8。

4、从 5 往上回溯到 2，在回溯到 1，发现 1 还有节点 43 未遍历，所以此时沿着 3， 6，9 进行遍历,这样就遍历完成了。

以下是用二叉树为例分别用递归和非递归来实现深度优先遍历

public class TestDfs {
    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

    public static void main(String[] args) {
        TreeNode tenNode = new TreeNode(10);
        TreeNode nineNode = new TreeNode(9);
        TreeNode eightNode = new TreeNode(8);
        TreeNode sevenNode = new TreeNode(7);
        TreeNode sixNode = new TreeNode(6);
        TreeNode fiveNode = new TreeNode(5);
        TreeNode fourNode = new TreeNode(4);
        TreeNode threeNode = new TreeNode(3);
        TreeNode twoNode = new TreeNode(2);
        TreeNode oneNode = new TreeNode(1);

        oneNode.left = twoNode;
        oneNode.right = threeNode;
        twoNode.left = fourNode;
        twoNode.right = fiveNode;
        fiveNode.left = sevenNode;
        fiveNode.right = eightNode;
        sevenNode.right = tenNode;
        threeNode.right = sixNode;
        sixNode.left = nineNode;

        System.out.println("====递归深度优先搜索====");
        dfsRecursion(oneNode);

        System.out.println();

        System.out.println("====非递归深度优先搜索====");
        dfsNotRecursion(oneNode);

    }

    /**
     * 深度优先搜索（递归）
     * @param treeNode treeNode
     */
    private static void dfsRecursion(TreeNode treeNode){
        //此处处理value值
        if(treeNode !=null){
            System.out.print(treeNode.val+" ");
        }else{
            return;
        }

        //递归当前节点的左节点
        dfsRecursion(treeNode.left);
        //递归当前节点的右节点
        dfsRecursion(treeNode.right);
    }

    /**
     * 非递归深度优先搜索
     * @param treeNode treeNode
     */
    private static void dfsNotRecursion(TreeNode treeNode){
        Stack<TreeNode> stack = new Stack<>();
        stack.push(treeNode);

        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            //此处处理value值
            System.out.print(node.val+" ");

            //栈为先入后出原则，为了保证先遍历左节点，所以先压入右节点，后压入左节点
            if(node.right != null){
                stack.push(node.right);
            }
            if(node.left != null){
                stack.push(node.left);
            }
        }
    }
}

运行结果：
====递归深度优先搜索====
1 2 4 5 7 10 8 3 6 9 
====非递归深度优先搜索====
1 2 4 5 7 10 8 3 6 9 

非递归深度优先搜索步骤
1、1入栈
栈元素：1

2、1出栈，打印1，oneNode子节点入栈
栈元素：3、2

3、2出栈，打印2，twoNode子节点入栈
栈元素：3、5、4

3、4出栈，打印4，fourNode自己点入栈（没有子节点）
栈元素：3、5

4、5出栈，打印5，fiveNode子节点入栈
栈元素：3、8、7

5、7出栈，打印7，sevenNode子节点入栈
栈元素：3、8、10

6、10出栈，打印10，tenNode子节点入栈（没有子节点）
栈元素：3、8

7、8出栈，打印8，eightNode子节点入栈（没有子节点）
栈元素：3

8、3出栈，打印3，threeNode子节点入栈
栈元素：6

9、6出栈，打印6，sixNode子节点入栈
栈元素：9

10、9出栈，打印9，nineNode子节点入栈（没有子节点）
栈元素：

栈空，结束遍历

广度优先搜索（BFS）
从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点，下面使用广度优先遍历一颗树：

广度优先遍历也叫层序遍历，先遍历第一层(节点 1)

再遍历第二层(节点 2、3)

第三层(4、5、6)

第四层(7、8、9)

第五层(10)

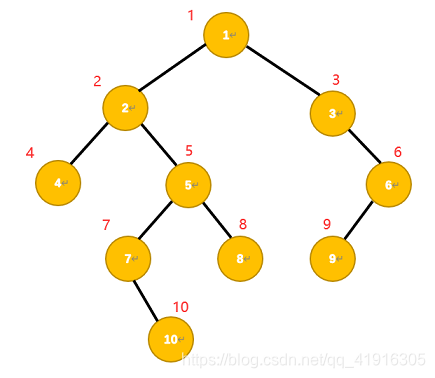
以下是用二叉树为例分别用队列来实现广度优先遍历

public class TestDfs {
    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode() {
        }

        TreeNode(int val) {
            this.val = val;
        }

        TreeNode(int val, TreeNode left, TreeNode right) {
            this.val = val;
            this.left = left;
            this.right = right;
        }
    }

    public static void main(String[] args) {
        TreeNode tenNode = new TreeNode(10);
        TreeNode nineNode = new TreeNode(9);
        TreeNode eightNode = new TreeNode(8);
        TreeNode sevenNode = new TreeNode(7);
        TreeNode sixNode = new TreeNode(6);
        TreeNode fiveNode = new TreeNode(5);
        TreeNode fourNode = new TreeNode(4);
        TreeNode threeNode = new TreeNode(3);
        TreeNode twoNode = new TreeNode(2);
        TreeNode oneNode = new TreeNode(1);

        oneNode.left = twoNode;
        oneNode.right = threeNode;
        twoNode.left = fourNode;
        twoNode.right = fiveNode;
        fiveNode.left = sevenNode;
        fiveNode.right = eightNode;
        sevenNode.right = tenNode;
        threeNode.right = sixNode;
        sixNode.left = nineNode;

        System.out.println("====非递归广度优先搜索====");
        bfsNotRecursion(oneNode);

    }

    /**
     * 非递归广度优先搜索
     * @param treeNode treeNode
     */
    private static void bfsNotRecursion(TreeNode treeNode){
        ArrayDeque<TreeNode> queue = new ArrayDeque<>();
        queue.add(treeNode);

        while (!queue.isEmpty()){
            TreeNode node = queue.poll();
            System.out.print(node.val + " ");

            if(node.left != null){
                queue.add(node.left);
            }
            if(node.right != null){
                queue.add(node.right);
            }
        }
    }
}

运行结果：
====非递归广度优先搜索====
1 2 3 4 5 6 7 8 9 10 

队列实现广度优先搜索步骤
1、1入队
队元素：1

2、1出队，打印1，oneNode子节点入队
队元素：2、3

3、2出队，打印2，twoNode子节点入队
队元素：3、4、5

3、3出队，打印3，threeNode子节点入队
队元素：4、5、6

4、4出队，打印4，fourNode子节点入队（没有子节点）
队元素：5、6

5、5出队，打印5，fiveNode子节点入队
队元素：6、7、8

6、6出队，打印6，sixNode子节点入队
队元素：7、8、9

7、7出队，打印7，sevenNode子节点入队
队元素：8、9、10

8、8出队，打印8，eightNode子节点入队（没有子节点）
队元素：9、10

9、9出队，打印9，nineNode子节点入队（没有子节点）
队元素：10

10、10出队，打印10，tenNode子节点入队（没有子节点）
队元素：

队空，结束遍历

转载于：https://www.ycblog.top/article?articleId=151&pageNum=1